Basic Trigonometric Functions and Identities | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year PDF Download
We’ve used the unit circle to define the trigonometric functions for acute angles so far. We’ll need more than acute angles in the next section where we’ll look at oblique triangles. Some oblique triangles are obtuse and we’ll need to know the sine and cosine of obtuse angles. As long as we’re doing that, we should also define the trig functions for angles beyond 180° and for negative angles. First we need to be clear about what such angles are.
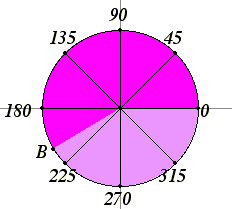
The ancient Greek geometers only considered angles between 0° and 180°, and they considered neither the straight angle of 180° nor the degenerate angle of 0° to be angles. It’s not only useful to consider those special cases to be angles, but also to include angles between 180° and 360°, too, sometimes called “reflex angles.” With the applications of trigonometry to the subjects of calculus and differential equations, angles beyond 360° and negative angles became accepted, too.
Consider the unit circle. Denote its center (0,0) as O, and denote the point (1,0) on it as A. As a moving point B travels around the unit circle starting at A and moving in a counterclockwise direction, the angle AOB as a 0° angle and increases. When B has made it all the way around the circle and back to A, then angle AOB is a 360° angle. Of course, this is the same angle as a 0° angle, so we can identify these two angles. As B continues the second time around the circle, we get angles ranging from 360° to 720°. They’re the same angles we saw the first time around, but we have different names for them. For instance, a right angle is named as either 90° or 450°. Each time around the circle, we get another name for the angle. So 90°, 450°, 810° and 1170° all name the same angle.
If B starts at the same point A and travels in the clockwise direction, then we’ll get negative angles, or more precisely, names in negative degrees for the same angles. For instance, if you go a quarter of a circle in the clockwise direction, the angle AOB is named as –90°. Of course, it’s the same as a 270° angle.
So, in summary, any angle is named by infinitely many names, but they all differ by multiples of 360° from each other.
Sines and cosines of arbitrary angles
Now that we have specified arbitrary angles, we can define their sines and cosines. Let the angle be placed so that its vertex is at the center of the unit circle O = (0,0), and let the first side of the angle be placed along the x-axis. Let the second side of the angle intersect the unit circle at B. Then the angle equals the angle AOB where A is (1,0). We use the coordinates of B to define the cosine of the angle and the sine of the angle. Specifically, the x-coordinate of B is the cosine of the angle, and the y-coordinate of B is the sine of the angle.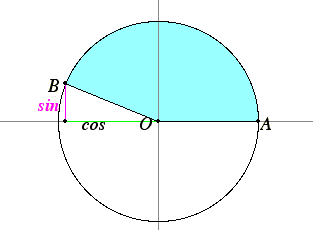
This definition extends the definitions of sine and cosine given before for acute angles.
Properties of sines and cosines that follow from this definition
There are several properties that we can easily derive from this definition. Some of them generalize identities that we have seen already for acute angles.
1. Sine and cosine are periodic functions of period 360°, that is, of period 2π. That’s because sines and cosines are defined in terms of angles, and you can add multiples of 360°, or 2π, and it doesn’t change the angle. Thus, for any angle θ,
sin (θ + 360°) = sin θ, and
cos (θ + 360°) = cos θ.
Many of the modern applications of trigonometry follow from the uses of trig to calculus, especially those applications which deal directly with trigonometric functions. So, we should use radian measure when thinking of trig in terms of trig functions. In radian measure that last pair of equations read as
sin (θ + 2π) = sin θ, and
cos (θ + 2π) = cos θ.
2. Sine and cosine are complementary:
cos θ = sin (π/2 – θ)
sin θ = cos (π/2 – θ)
We’ve seen this before, but now we have it for any angle θ. It’s true because when you reflect the plane across the diagonal line y = x, an angle is exchanged for its complement.
3. The Pythagorean identity for sines and cosines follows directly from the definition. Since the point B lies on the unit circle, its coordinates x and y satisfy the equation x2 + y2 =1. But the coordinates are the cosine and sine, so we conclude
sin2 θ + cos2 θ = 1.
We’re now ready to look at sine and cosine as functions.
4. Sine is an odd function, and cosine is an even function. You may not have come across these adjectives “odd” and “even” when applied to functions, but it’s important to know them. A function f is said to be an odd function if for any number x, f(–x) = –f(x). A function f is said to be an even function if for any number x, f(–x) = f(x). Most functions are neither odd nor even functions, but some of the most important functions are one or the other. Any polynomial with only odd degree terms is an odd function, for example, f(x) = x5 + 8x3 – 2x. (Note that all the powers of x are odd numbers.) Similarly, any polynomial with only even degree terms is an even function. For example, f(x) = x4 – 3x2 – 5. (The constant 5 is 5x0, and 0 is an even number.)
Sine is an odd function, and cosine is even
sin (–θ) = –sin θ, and
cos (–θ) = cos θ.
These facts follow from the symmetry of the unit circle across the x-axis. The angle –t is the same angle as t except it’s on the other side of the x-axis. Flipping a point (x,y) to the other side of the x-axis makes it into (x,–y), so the y-coordinate is negated, that is, the sine is negated, but the x-coordinate remains the same, that is, the cosine is unchanged.
5. An obvious property of sines and cosines is that their values lie between –1 and 1. Every point on the unit circle is 1 unit from the origin, so the coordinates of any point are within 1 of 0 as well.
The graphs of the sine and cosine functions
Let’s use t as a variable angle. You can think of t as both an angle as as time. A good way for human beings to understand a function is to look at its graph. Let’s start with the graph of sin t. Take the horizontal axis to be the t-axis (rather than the x-axis as usual), take the vertical axis to be the y-axis, and graph the equation y = sin t. It looks like this.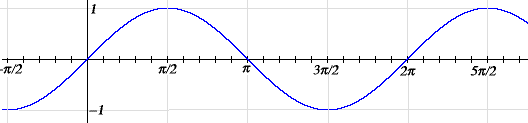
Fig. Sine Wave
First, note that it is periodic of period 2π. Geometrically, that means that if you take the curve and slide it 2π either left or right, then the curve falls back on itself. Second, note that the graph is within one unit of the t-axis. Not much else is obvious, except where it increases and decreases. For instance, sin t grows from 0 to π/2 since the y-coordinate of the point B increases as the angle AOB increases from 0 to π/2.
Next, let’s look at the graph of cosine. Again, take the horizontal axis to be the t-axis, but now take the vertical axis to be the x-axis, and graph the equation x = cos t.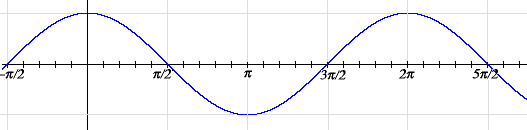
Fig. Cosine Wave
Note that it looks just like the graph of sin t except it’s translated to the left by π/2. That’s because of the identity cos t = sin (π/2 + t). Although we haven’t come across this identity before, it easily follows from ones that we have seen: cos t = cos –t = sin (π/2 – (–t)) = sin (π/2 + t).
The graphs of the tangent and cotangent functions
The graph of the tangent function has a vertical asymptote at x = π/2. This is because the tangent approaches infinity as t approaches π/2. (Actually, it approaches minus infinity as t approaches π/2 from the right as you can see on the graph.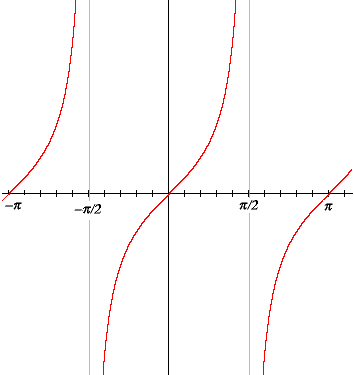
Fig. Tangent
You can also see that tangent has period π; there are also vertical asymptotes every π units to the left and right. Algebraically, this periodicity is expressed by tan (t + π) = tan t.
The graph for cotangent is very similar.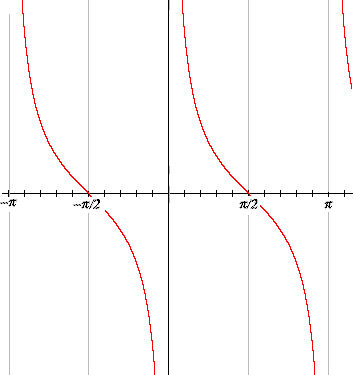
This similarity is simply because the cotangent of t is the tangent of the complementary angle π – t.
The graphs of the secant and cosecant functions
The secant is the reciprocal of the cosine, and as the cosine only takes values between –1 and 1, therefore the secant only takes values above 1 or below –1, as shown in the graph. Also secant has a period of 2π.
the graph of y = sec x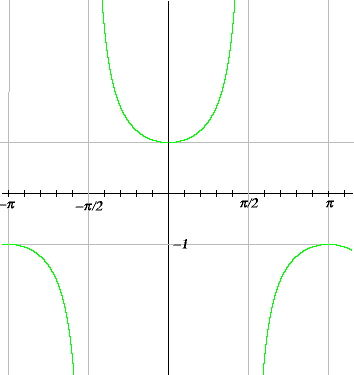
As you would expect by now, the graph of the cosecant looks much like the graph of the secant.
Trigonometric Identities :
In mathematics, trigonometric identities are equalities where we would have trigonometric functions and they would be true for every value of the occurring variables. Geometrically, these are identities involving certain functions of one or more angles.
Trigonometric Identities
Sin θ = Opposite side / Hypotenuse side
Cos θ = Adjacent side / Hypotenuse side
Tan θ = Opposite side / Adjacent side
Csc θ = Hypotenuse side / Opposite side
Sec θ = Hypotenuse side / Adjacent side
Cot θ = Adjacent side / Opposite side
Reciprocal Trigonometric Identities
Sinθ = 1 / Cosecθ
Cscθ = 1 / Sinθ
Cosθ = 1 / Secθ
Secθ = 1 / Cosθ
Tanθ = 1 / Cotθ
Cotθ = 1 / Tanθ
Other Trigonometric Identities
Sin²θ + Cos²θ = 1
Sin²θ = 1 - Cos²θ
Cos²θ = 1 - Sin²θ
Sec²θ - Tan²θ = 1
Sec²θ = 1 + Tan²θ
Tan²θ = Sec²θ - 1
Csc²θ - Cot²θ = 1
Csc²θ = 1 + Cot²θ
Cot²θ = Csc²θ - 1
Double Angle Identities
Sin2A = 2 ⋅ SinA ⋅ CosA
Cos2A = Cos²A - Sin²A
Tan2A = 2 ⋅ TanA / (1 - Tan²A)
Cos2A = 1 - 2 ⋅ Sin²A
Cos2A = 2 ⋅ Cos²A - 1
Sin2A = 2 ⋅ TanA / (1 + Tan²A)
Cos2A = (1 - Tan²A) / (1 + Tan²A)
Sin²A = (1 - Cos2A) / 2
Cos²A = (1 + Cos2A) / 2
Half Angle Identities
SinA = 2 ⋅ Sin(A/2) ⋅ Cos(A/2)
CosA = Cos²(A/2) - Sin²(A/2)
TanA = 2 ⋅ Tan(A/2) / [1 - Tan²(A/2)]
CosA = 1 - 2 ⋅ Sin²(A/2)
CosA = 2 ⋅ Cos²(A/2) - 1
SinA = 2 ⋅ Tan(A/2) / [1 + Tan²(A/2)]
CosA = [1 - Tan²(A/2)] / [1 + Tan²(A/2)]
Sin²A/2 = (1 - Cos A) / 2
Cos²A/2 = (1 + Cos A) / 2
Tan²(A/2) = (1 - CosA) / (1 + CosA)
Compound Angles Identities
Sin(A + B) = SinA ⋅ CosB + CosA ⋅ SinB
Sin(A + B) = SinA ⋅ CosB + CosA ⋅ SinB
Cos(A + B) = CosA ⋅ CosB - SinA ⋅ SinB
Cos(A - B) = CosA ⋅ CosB + SinA ⋅ SinB
Tan(A + B) = [TanA + TanB] / [1- TanA ⋅ TanB]
Tan(A - B) = [TanA - TanB] / [1 + TanA ⋅ TanB]
Sum to Product Identities
SinC + SinD = 2 ⋅ Sin[(C+D) / 2] ⋅ cos [(C-D) / 2]
SinC - SinD = 2 ⋅ Cos [(C+D) / 2] ⋅ Sin [(C-D) / 2
CosC + CosD = 2 ⋅ Cos [(C+D) / 2] ⋅ Cos [(C-D) / 2]
CosC - CosD = 2 ⋅ Sin [(C+D) / 2] ⋅ Sin [(C-D) / 2]
Triple Angle Identities
Sin3A = 3 ⋅ SinA - 4 ⋅ sin³A
Cos3A = 4 ⋅ Cos³A - 3 ⋅ Cos A
Tan3A = [3 ⋅ TanA - Tan³A] / [1 - 3 ⋅ Tan²A]
Values of Certain Angles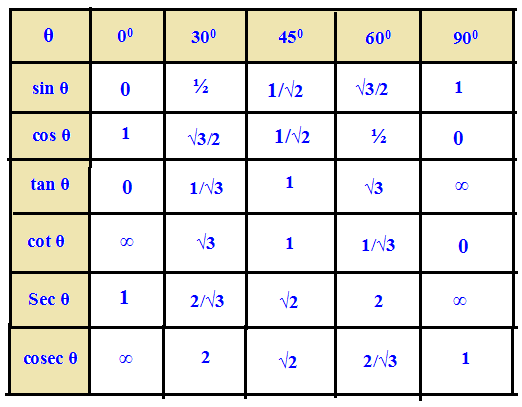
Solving Word Problems Using Trigonometric Identities
Step 1 : Understanding the question and drawing the appropriate diagram are the two most important things to be done in solving word problems in trigonometry.
Step 2 : If it is possible, we have to split the given information. Because, when we split the given information in to parts, we can understand them easily.
Step 3 : We have to draw diagram almost for all of the word problems in trigonometry. The diagram we draw for the given information must be correct. Drawing diagram for the given information will give us a clear understanding about the question.
Step 4 : Once we understand the given information clearly and correct diagram is drawn, solving word problems in trigonometry would not be a challenging work.
Step 5 : After having drawn the appropriate diagram based on the given information, we have to give name for each position of the diagram using English alphabets (it is clearly shown in the word problem given below). Giving name for the positions would be easier for us to identify the parts of the diagram.
Step 6 : Now we have to use one of the three trigonometric ratios (sin, cos and tan) to find the unknown side or angle.
Once the diagram is drawn and we have translated the English Statement (information) given in the question as mathematical equation using trigonometric ratios correctly, 90% of the work will be over. The remaining 10% is just getting the answer. That is solving for the unknown.
Trigonometry word problems with solutions
Problem 1 : The angle of elevation of the top of the building at a distance of 50 m from its foot on a horizontal plane is found to be 60 degree. Find the height of the building.
Solution :
First let us draw a figure for the information given in the question.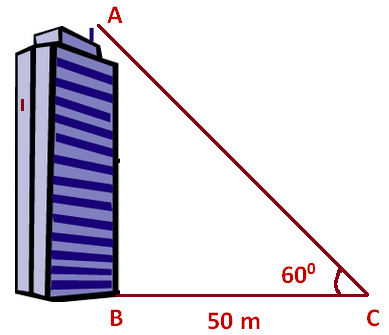
Here, AB represents height of the building, BC represents distance of the building from the point of observation.
In the right triangle ABC, the side which is opposite to the angle 60 degree is known as opposite side (AB), the side which is opposite to 90 degree is called hypotenuse side (AC) and the remaining side is called adjacent side (BC).
Now we need to find the length of the side AB.
tanθ = Opposite side/Adjacent side
tan 60° = AB/BC
√3 = AB/50
√3 x 50 = AB
AB = 50√3
Approximate value of √3 is 1.732
AB = 50 (1.732)
AB = 86.6 m
Hence, the height of the building is 86.6 m
Problem 2 : A ladder placed against a wall such that it reaches the top of the wall of height 6 m and the ladder is inclined at an angle of 60 degree. Find how far the ladder is from the foot of the wall.
Solution :
First let us draw a figure for the information given in the question.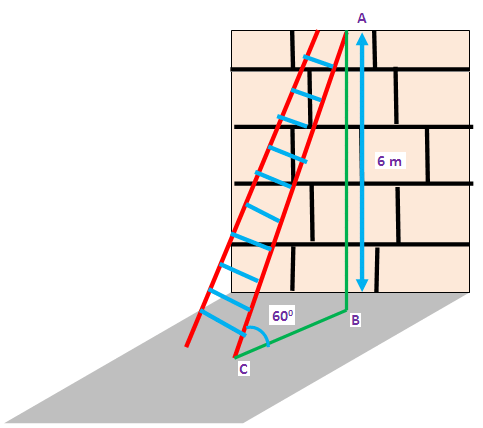
Here AB represents height of the wall, BC represents the distance between the wall and the foot of the ladder and AC represents the length of the ladder.
In the right triangle ABC, the side which is opposite to angle 60 degree is known as opposite side (AB), the side which is opposite to 90 degree is called hypotenuse side (AC) and remaining side is called adjacent side (BC).
Now, we need to find the distance between foot of the ladder and the wall. That is, we have to find the length of BC.
tan θ = Opposite side/Adjacent side
tan60° = AB/BC
√3 = 6/BC
BC = 6/√3
BC = (6/√3) x (√3/√3)
BC = (6√3)/3
BC = 2√3
Approximate value of √3 is 1.732
BC = 2 (1.732)
BC = 3.464 m
Hence, the distance between foot of the ladder and the wall is 3.464 m
Problem 3 : A string of a kite is 100 meters long and it makes an angle of 60° with horizontal. Find the height of the kite,assuming that there is no slack in the string.
Solution :
First let us draw a figure for the information given in the question.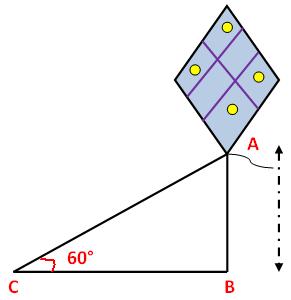
Here AB represents height of kite from the ground, BC represents the distance of kite from the point of observation.
In the right triangle ABC the side which is opposite to angle 60 degree is known as opposite side (AB), the side which is opposite to 90 degree is called hypotenuse side (AC) and remaining side is called adjacent side (BC).
Now we need to find the height of the side AB.
Sin θ = Opposite side/Hypotenuse side
sinθ = AB/AC
sin 60° = AB/100
√3/2 = AB/100
(√3/2) x 100 = AB
AB = 50 √3 m
Hence, the height of kite from the ground 50 √3 m
Problem 4 : From the top of the tower 30 m height a man is observing the base of a tree at an angle of depression measuring 30 degree. Find the distance between the tree and the tower.
Solution :
First let us draw a figure for the information given in the question.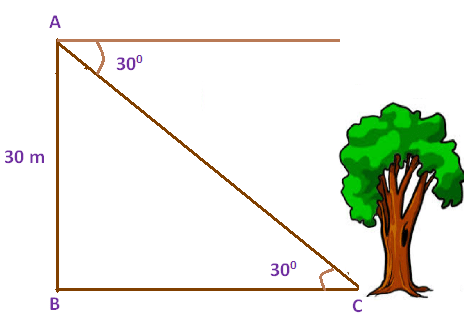
Here AB represents height of the tower, BC represents the distance between foot of the tower and the foot of the tree.Now we need to find the distance between foot of the tower and the foot of the tree (BC).tan θ = Opposite side/Adjacent sidetan 30° = AB/BC
1/√3 = 30/BC
BC = 30√3
Approximate value of √3 is 1.732
BC = 30 (1.732)
BC = 81.96 m
Hence, the distance between the tree and the tower is 51.96 m
Problem 5 : A man wants to determine the height of a light house. He measured the angle at A and found that tan A = 3/4. What is the height of the light house if A is 40 m from the base?
Solution :
First let us draw a figure for the information given in the question.

Here BC represents height of the light house, AB represents the distance between the light house from the point of observation.
In the right triangle ABC the side which is opposite to the angle A is known as opposite side (BC), the side which is opposite to 90 degree is called hypotenuse side (AC) and remaining side is called adjacent side (AB).
Now we need to find the height of the light house (BC).
tanA = Opposite side/Adjacent side
tanA = BC/AB
Given : tanA = 3/4
3/4 = BC/40
3 x 40 = BC x 4
BC = (3 x 40)/4
BC = (3 x 10)
BC = 30 m
Hence, the height of the light house is 30 m
Problem 6 : A man wants to determine the height of a light house. He A ladder is leaning against a vertical wall makes an angle of 20° with the ground. The foot of the ladder is 3 m from the wall.Find the length of ladder.
Solution :
First let us draw a figure for the information given in the question.
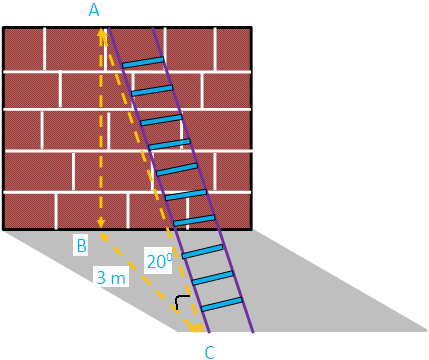
Here AB represents height of the wall, BC represents the distance of the wall from the foot of the ladder.
In the right triangle ABC the side which is opposite to the angle 20 degree is known as opposite side (AB),the side which is opposite to 90 degree is called hypotenuse side (AC) and remaining side is called adjacent side (BC).
Now we need to find the length of the ladder (AC).
Cos θ = Adjacent side/Hypotenuse side
Cos θ = BC/AC
Cos 20° = 3/AC
0.9396 = 3/AC
AC = 3/0.9396
AC = 3.192
Hence, the The length of the ladder is 3.192 m. trigono
Problem 7 : A kite flying at a height of 65 m is attached to a string inclined at 31° to the horizontal. What is the length of string ?
Solution :
First let us draw a figure for the information given in the question.
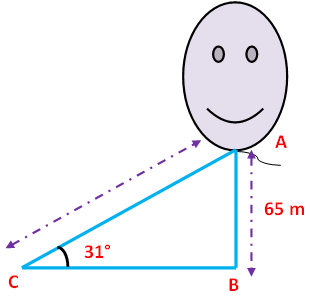
Here AB represents height of the kite. In the right triangle ABC the side which is opposite to angle 31 degree is known as opposite side (AB), the side which is opposite to 90 degree is called hypotenuse side (AC) and the remaining side is called adjacent side (BC).
Now we need to find the length of the string AC.
Sin θ = Opposite side/Hypotenuse side
Sin θ = AB/AC
Sin 31° = AB/AC
0.5150 = 65/AC
AC = 65/0.5150
AC = 126.2 m
Hence, the length of the string is 126.2 m
Problem 8 : The length of a string between a kite and a point on the ground is 90 m. If the string is making an angle θ with the level ground such that tan θ = 15/8, how high will the kite be ?
Solution :
First let us draw a figure for the information given in the question.
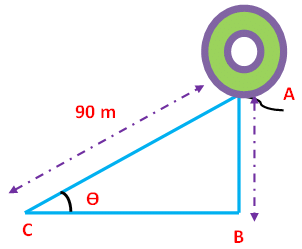
Here AB represents height of the balloon from the ground. In the right triangle ABC the side which is opposite to angle θ is known as opposite side (AB), the side which is opposite to 90 degree is called hypotenuse side (AC) and remaining side is called adjacent side (BC).
Now we need to find the length of the side AB.
Tan θ = 15/8 --------> Cot θ = 8/15
Csc θ = √(1+ cot²θ)
Csc θ = √(1 + 64/225)
Csc θ = √(225 + 64)/225
Csc θ = √289/225
Csc θ = 17/15 -------> Sin θ = 15/17
But, sin θ = Opposite side/Hypotenuse side = AB/AC
AB/AC = 15/17
AB/90 = 15/17
AB = (15 x 90)/17
AB = 79.41
Hence, the height of the tower is 79.41 m
Problem 9 : An aeroplane is observed to be approaching the airpoint. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 50 degree. Find the height above the ground.
Solution :
First let us draw a figure for the information given in the question.
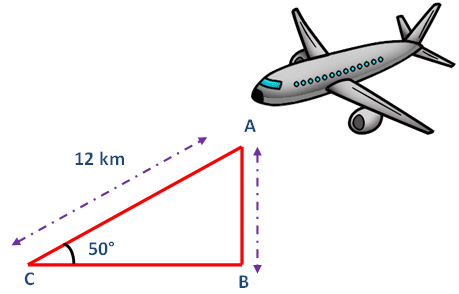
Here AB represents height of the airplane from the ground.In the right triangle ABC the side which is opposite to angle 50 degree is known as opposite side (AB), the side which is opposite to 90 degree is called hypotenuse side (AC) and remaining side is called adjacent side (BC).
Now we need to find the length of the side AB.
From the figure given above, AB stands for the height of the aeroplane above the ground.
sin θ = Opposite side/Hypotenuse side
sin 50° = AB/AC
0.7660 = h/12
0.7660 x 12 = h
h = 9.192 km
Hence, the height of the aeroplane above the ground is 9.192 km
Problem 10 : A balloon is connected to a meteorological station by a cable of length 200 m inclined at 60 degree angle . Find the height of the balloon from the ground. (Imagine that there is no slack in the cable)
Solution :
First let us draw a figure for the information given in the question.
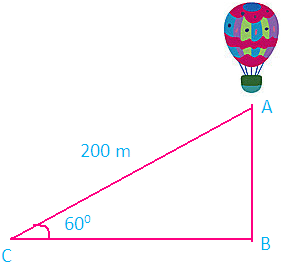
Here AB represents height of the balloon from the ground. In the right triangle ABC the side which is opposite to angle 60 degree is known as opposite side (AB), the side which is opposite to 90 degree is called hypotenuse (AC) and the remaining side is called as adjacent side (BC).
Now we need to find the length of the side AB.
From the figure given above, AB stands for the height of the balloon above the ground.
sin θ = Opposite side/Hypotenuse side
sin θ = AB/AC
sin 60° = AB/200
√3/2 = AB/200
AB = (√3/2) x 200
AB = 100√3
Approximate value of √3 is 1.732
AB = 100 (1.732)
AB = 173.2 m
Hence, the height of the balloon from the ground is 173.2 m
|
1335 videos|1432 docs|834 tests
|
FAQs on Basic Trigonometric Functions and Identities - SSC CGL Tier 2 - Study Material, Online Tests, Previous Year
| 1. What are the basic trigonometric functions? |  |
| 2. How do you find the sine, cosine, and tangent of an angle? |  |
| 3. What are the trigonometric identities? |  |
| 4. How do you prove trigonometric identities? |  |
| 5. What are some applications of trigonometric functions? |  |
















