Basics of Complex Numbers | Algebra - Mathematics PDF Download
| Table of contents |

|
| Complex Numbers - Introduction |

|
| Why So Complex? |

|
| Equality of Complex Numbers |

|
| More Solved Examples For You |

|
Complex Numbers - Introduction
Let us try and solve the equation x2+1 =0. We can simplify it and write it as x2=-1 or x = ± √−1.
But what is the root of -1?
It is not on the number line.
So does it simply not exist?
Well in mathematics, sticking to reality has never been a priority!
- This solution does not lie on the number line, that means it must be off it then.
- We can write -a = (-1)×(a), where ‘a’ is a real number.
- The square root of a negative number can be written as
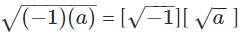
- Let us use a symbol for √−1. Let’s denote it by ‘i’ ( from iota, Greek for extremely small).
- Then i = √−1 is a number that doesn’t fall anywhere on the number line!
- Such numbers that are not on the real number line, are the imaginary numbers. They are also known as the complex numbers.
“Now wait for a second, we only have ‘i’, why are you calling it numbers? Where are the others?”
We can get every real number from other real numbers by certain algebraic operations.
- Like if you keep on adding the number one to itself, you will get the set of natural numbers and so on.
- Similarly, all the numbers that have ‘i’ in them are the imaginary numbers.
- The number i, is the imaginary unit. 3i, 4i, -i, √−9 etc. are all imaginary numbers.
Let us have a general definition of the imaginary or complex numbers.
Why So Complex?
Let ‘a’ , ‘b’ be two real numbers. Let i = √−1, then any number of the form a + ib is a complex number.
- The reason to define a complex number in this way is to make a connection between the real numbers and the complex ones. For example, we can write, 2 = 2 + 0.i. Therefore, every real number can be written in the form of a + ib; where b = 0.
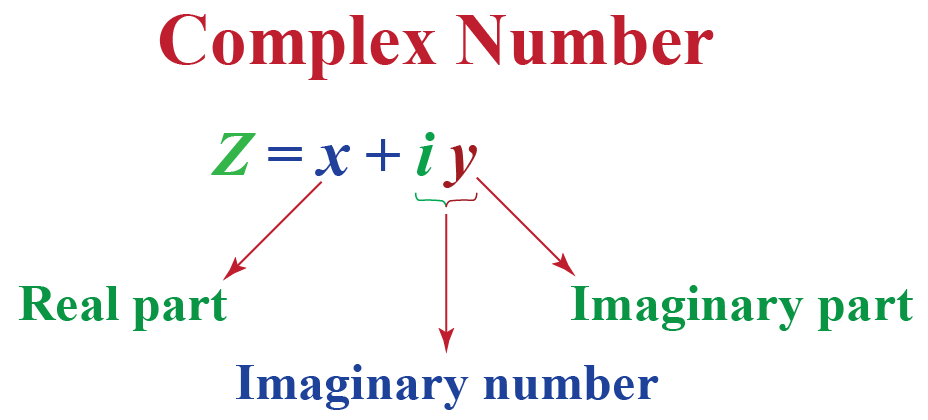
- Also if a complex number is such that a = 0, we call it a purely imaginary number. In general, a is known as the “real” part and b is known as the “imaginary” or the complex part of the imaginary number.
- “Why am I doing this again?” Well, hold on.
Let’s recall the equation that we couldn’t quite figure out the solution for i.e. x2+1=0.
- Hence, x = ± √−1 or x = ± i. Substituting for x, in the equation we have (i)2+1=0
i2 =±[√−1]2=-1, using the above equation we have, (-1)+1=0 satisfies the equation. - Substitution of -i also gives the same results. So there you go, now you can solve equations that you would have rather just left alone.
To sum up, all the numbers of the form a +ib, where a and b are real and i =√−1 , are called imaginary numbers. We usually denote an imaginary number by ‘z’.
Equality of Complex Numbers
Let us practice the concepts we have read this far.
Example: There are two numbers z1 = x + iy and z2 = 3 – i7. Find the value of x and y for z1 = z2. What is the sum of Re (z1, z2)?
Sol: We have z1 = x + iy and z2 = 3 – i7.
- First of all, real part of any complex number (a+ib) is represented as Re(a + ib) = a and imaginary part of (a +ib) is represented as Im(a+ib) = b.
- Also, when two complex numbers are equal, their corresponding real parts and imaginary parts must be equal. Therefore, if a + ib = c + id, then Re(a+ib) = Re(c+id) and Im(a+ib) = Im(c+id)
- Conversely if two complex numbers say z1 and z2, are such that Re(z1) = Re(z2) and Im(z1) = Im(z2), then z1=z2. In other words, we must have a = c and b = d. We can’t have a = d because we can’t relate the real and the imaginary parts together. Let us come back to our problem.
z1 = z2 or x + iy = 3 – i7
Re(x + iy) = x Re(3 – i7) = 3
Im(x + iy) = y Im(3 – i7) = -7- This means x = 3 and y = -7. Therefore, Re(z1,z2) = 3,3 and hence, the sum of real parts of z1 and z2 = 3 + 3 = 6.
- Integer Powers of ‘i’ - As we saw already, i2 = -1. Also, i3 = i2(i) = -i. Similarly, you can find any given power of i, by reducing it to the above two forms.
More Solved Examples For You
Example 1: If 2i2+6i3+3i16−6i19+4i25=x+iy, then (x,y)= ?
A) (1 , 4)
B) (4 , 1)
C) (-1 , 4)
D) (-1 , -4)
Ans: (A)
Sol: The above expression can be simplified as:2 (-1) + 6 (-i) + 3 ( i )2×2×2×2 – 6 (i18 . i) + 4 (i24.i) = x + iy
Therefore, -2 – 6i + 3 (1) – 6 (-1)9.i + 4i = x + iy Or 1 + 4i = x + iy
Therefore, x = 1 and y = 4 or (x,y) = (1,4)
Example 2: Perform the indicated operation and write your answer in standard form.
(4−5i)(12+11i)
Sol: We know how to multiply two polynomials and so we also know how to multiply two complex numbers. All we need to do is “foil” the two complex numbers to get,
(4−5i)(12+11i) = 48+44i−60i−55i2 = 48−16i−55i2
All we need to do to finish the problem is to recall that i2=−1. Upon using this fact we can finish the problem.
(4−5i)(12+11i)=48−16i−55(−1)=103−16i
Example 3: If |z| = 1, and ||z² + 2z + 6 + 8i| ≤ n, then value of n is ______. (Here, z = x + it)
Sol: We have, |z₁ + z₂ + z₃ + ... + zₙ| ≤ |z₁| + |z₂| + |z₃| + ... + |zₙ|
Hence, |z² + 2z + 6 + 8i| ≤ |z²| + 2|z| + |6 + 8i| ≤ |z²| + 2|z| + √(36 + 64) ≤ 13
Therefore, n = 13
|
181 videos|58 docs
|
FAQs on Basics of Complex Numbers - Algebra - Mathematics
| 1. What are complex numbers and how are they used in mathematics? |  |
| 2. How do you determine the equality of complex numbers? |  |
| 3. What is the geometric representation of complex numbers? |  |
| 4. How do you perform basic operations (addition, subtraction, multiplication, division) with complex numbers? |  |
| 5. What are some applications of complex numbers in real life? |  |





















