Basics of Sequence | Algebra - Mathematics PDF Download
Sequence - Introduction
Let’s start off this section with a discussion of just what a sequence is.
A sequence is nothing more than a list of numbers written in a specific order.
- The list may or may not have an infinite number of terms in them although we will be dealing exclusively with infinite sequences in this class.
- General sequence terms are denoted as follows,
a1 — second term
a2 — second term
an — nth term
an+1 — (n+1)st term - Because we will be dealing with infinite sequences each term in the sequence will be followed by another term as noted above.
- In the notation above we need to be very careful with the subscripts. The subscript of n+1 denotes the next term in the sequence and NOT one plus the nth term!
- In other words,
 , so be very careful when writing subscripts to make sure that the “+1” doesn’t migrate out of the subscript! This is an easy mistake to make when you first start dealing with this kind of thing.
, so be very careful when writing subscripts to make sure that the “+1” doesn’t migrate out of the subscript! This is an easy mistake to make when you first start dealing with this kind of thing. - There is a variety of ways of denoting a sequence. Each of the following is equivalent way of denoting a sequence.

- In the second and third notations above an is usually given by a formula.
A couple of notes are now in order about these notations.
- Note the difference between the second and third notations above.
- If the starting point is not important or is implied in some way by the problem it is often not written down as we did in the third notation.
- Next, we used a starting point of n =1 in the third notation only so we could write one down.
- There is absolutely no reason to believe that a sequence will start at n =1.
- A sequence will start where ever it needs to start.
Let’s take a look at a couple of sequences.
Example: Write down the first few terms of each of the following sequences.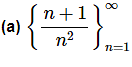
Solution. To get the first few sequence terms here all we need to do is plug in values of n into the formula given and we’ll get the sequence terms.
Note the inclusion of the “…” at the end! This is an important piece of notation as it is the only thing that tells us that the sequence continues on and doesn’t terminate at the last term.
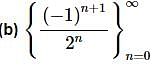
Solution. This one is similar to the first one. The main difference is that this sequence doesn’t start at n=1.
Note that the terms in this sequence alternate in signs. Sequences of this kind are sometimes called alternating sequences.

Solution. This sequence is different from the first two in the sense that it doesn’t have a specific formula for each term. However, it does tell us what each term should be. Each term should be the nth digit of p. So we know that π = 3.14159265359…
The sequence is then,
In the first two parts of the previous example note that we were really treating the formulas as functions that can only have integers plugged into them. Or,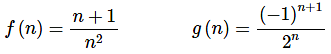
This is an important idea in the study of sequences (and series).
Some Important Ideas
Treating the sequence terms as function evaluations will allow us to do many things with sequences that we couldn’t do otherwise. Before delving further into this idea however, we need to get a couple more ideas out of the way.
Let's discuss “graphing” a sequence.
To graph the sequence {an}we plot the points (n,an) as n ranges over all possible values on a graph. For instance, let’s graph the sequence 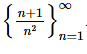 . The first few points on the graph are,
. The first few points on the graph are,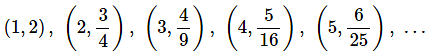
The graph, for the first 30 terms of the sequence, is then,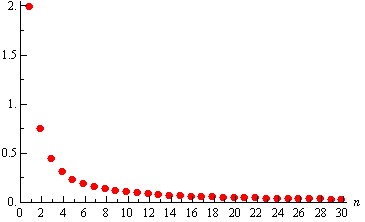
- This graph leads us to an important idea about sequences.
- Notice that as n increases the sequence terms in our sequence, in this case, get closer and closer to zero.
- We then say that zero is the limit (or sometimes the limiting value) of the sequence and write,

This notation should look familiar to you. It is the same notation we used when we talked about the limit of a function. - In fact, if you recall, we said earlier that we could think of sequences as functions in some way and so this notation shouldn’t be too surprising.
Using the ideas that we developed for limits of functions we can write down the following working definition for limits of sequences.
Working Definition of Limit
1. We say that ,
,
if we can make an as close to L as we want for all sufficiently large n. In other words, the value of the an’s approach L as n approaches infinity.
2. We say that ,
,
if we can make an as large as we want for all sufficiently large n. Again, in other words, the value of the an’s get larger and larger without bound as n approaches infinity.
3. We say that ,
,
if we can make an as large and negative as we want for all sufficiently large n. Again, in other words, the value of the an’s are negative and get larger and larger without bound as n approaches infinity.
The working definitions of the various sequence limits are nice in that they help us to visualize what the limit actually is. Just like with limits of functions, however, there is also a precise definition for each of these limits. Let’s give those before proceeding.
Precise Definition of Limit
1. We say that  = L if for every number ε>0 there is an integer N such that
= L if for every number ε>0 there is an integer N such that

2. We say that  = ∞ if for every number M>0 there is an integer N such that
= ∞ if for every number M>0 there is an integer N such that
3. We say that  = -∞ if for every number M<0 there is an integer N such that
= -∞ if for every number M<0 there is an integer N such that
We won’t be using the precise definition often, but it will show up occasionally.
Note that both definitions tell us that in order for a limit to exist and have a finite value, all the sequence terms must be getting closer and closer to that finite value as n increases.
Terminology
Now that we have the definitions of the limit of sequences out of the way we have a bit of terminology that we need to look at.
- If
 exists and is finite we say that the sequence is convergent.
exists and is finite we say that the sequence is convergent. - If
 doesn’t exist or is infinite we say the sequence diverges.
doesn’t exist or is infinite we say the sequence diverges. - Note that sometimes we will say the sequence diverges to
 and if
and if  we will sometimes say that the sequence diverges to −∞.
we will sometimes say that the sequence diverges to −∞. - Get used to the terms “convergent” and “divergent” as we’ll be seeing them quite a bit throughout this chapter.
So just how do we find the limits of sequences? Most limits of most sequences can be found using one of the following theorems.
Theorem 1
Given the sequence {an} if we have a function f(x) such that f(n) = an and 
- This theorem is basically telling us that we take the limits of sequences much like we take the limit of functions.
- In fact, in most cases, we’ll not even really use this theorem by explicitly writing down a function.
- We will more often just treat the limit as if it were a limit of a function and take the limit as we always did back in Calculus I when we were taking the limits of functions.
So, now that we know that taking the limit of a sequence is nearly identical to taking the limit of a function we also know that all the properties from the limits of functions will also hold.
Properties
If {an} and {bn} are both convergent sequences then,

These properties can be proved using Theorem 1 above and the function limit properties we saw in Calculus I or we can prove them directly using the precise definition of a limit using nearly identical proofs of the function limit properties.
Next, just as we had a Squeeze Theorem for function limits, we also have one for sequences and it is pretty much identical to the function limit version.
Squeeze Theorem for Sequences

Note that in this theorem the “for all n>N for some N” is really just telling us that we need to have an≤cn≤bn for all sufficiently large n, but if it isn’t true for the first few n that won’t invalidate the theorem.
As we’ll see not all sequences can be written as functions that we can actually take the limit of. This will be especially true for sequences that alternate in signs. While we can always write these sequence terms as a function we simply don’t know how to take the limit of a function like that. The following theorem will help with some of these sequences.
Theorem 2

Note that in order for this theorem to hold the limit MUST be zero and it won’t work for a sequence whose limit is not zero. This theorem is easy enough to prove so let’s do that.
Proof of Theorem 2
The main thing to this proof is to note that,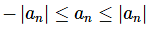
Then note that,
We then have  and so by the Squeeze Theorem we must also have,
and so by the Squeeze Theorem we must also have,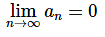
The next theorem is a useful theorem giving the convergence/divergence and value (for when it’s convergent) of a sequence that arises on occasion.
Theorem 3
The sequence  converges if −1<r≤1 and diverges for all other values of r. Also,
converges if −1<r≤1 and diverges for all other values of r. Also,
Here is a quick (well not so quick, but definitely simple) partial proof of this theorem.
Partial Proof of Theorem 3
We’ll do this through a series of cases although the last case will not be completely proven.
Case 1: r>1
We know from Calculus I that 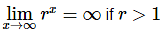 and so by Theorem 1 above we also know that
and so by Theorem 1 above we also know that 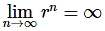 and so the sequence diverges if r>1.
and so the sequence diverges if r>1.
Case 2: r=1
In this case, we have,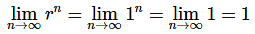
So, the sequence converges for r=1 and in this case its limit is 1.
Case 3 : 0<r<1
We know from Calculus I that 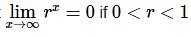 and so by Theorem 1 above we also know that
and so by Theorem 1 above we also know that  and so the sequence converges if 0<r<1 and in this case its limit is zero.
and so the sequence converges if 0<r<1 and in this case its limit is zero.
Case 4: r=0
In this case, we have,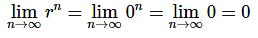
So, the sequence converges for r=0 and in this case its limit is zero.
Case 5: −1<r<0
First, let’s note that if −1<r<0 then 0<|r|<1 then by Case 3 above we have,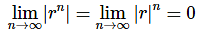
Theorem 2 above now tells us that we must also have,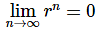 and so if −1<r<0 the sequence converges and has a limit of 0.
and so if −1<r<0 the sequence converges and has a limit of 0.
Case 6: r=−1
In this case, the sequence is,
and hopefully, it is clear that 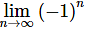 doesn’t exist. Recall that in order for this limit to exist the terms must be approaching a single value as n increases. In this case, however, the terms just alternate between 1 and -1 and so the limit does not exist.
doesn’t exist. Recall that in order for this limit to exist the terms must be approaching a single value as n increases. In this case, however, the terms just alternate between 1 and -1 and so the limit does not exist.
So, the sequence diverges for r=−1.
Case 7: r<−1.
In this case, we’re not going to go through complete proof.
Let’s just see what happens if we let r=−2 for instance. If we do that the sequence becomes,
So, if r=−2 we get a sequence of terms whose values alternate in sign and get larger and larger and so 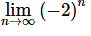 doesn’t exist. It does not settle down to a single value as n increases nor do the terms ALL approach infinity. So, the sequence diverges for r=−2.
doesn’t exist. It does not settle down to a single value as n increases nor do the terms ALL approach infinity. So, the sequence diverges for r=−2.
We could do something similar for any value of r such that r<−1 and so the sequence diverges for r<−1.
Examples:
Let’s take a look at a couple of examples of limits of sequences.
Example: Determine if the following sequences converge or diverge. If the sequence converges determine its limit.
Solution. To do a limit in this form all we need to do is factor from the numerator and denominator the largest power of n, cancel and then take the limit.
So, the sequence converges and its limit is 3/5.
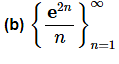
Solution.
- We will need to be careful with this one. We will need to use L’Hospital’s Rule on this sequence.
- The problem is that L’Hospital’s Rule only works on functions and not on sequences.
- Normally this would be a problem, but we’ve got Theorem 1 from above to help us out. Let’s define
 and note that,
and note that, .
. - Theorem 1 says that all we need to do is take the limit of the function.
 So, the sequence in this part diverges (to ∞).
So, the sequence in this part diverges (to ∞). - More often than not we just do L’Hospital’s Rule on the sequence terms without first converting to x’s since the work will be identical regardless of whether we use x or n.
- However, we really should remember that technically we can’t do the derivatives while dealing with sequence terms.
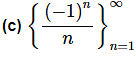
Solution.
- We will also need to be careful with this sequence. We might be tempted to just say that the limit of the sequence terms is zero (and we’d be correct).
- However, technically we can’t take the limit of sequences whose terms alternate in sign, because we don’t know how to do limits of functions that exhibit that same behaviour.
- Also, we want to be very careful to not rely too much on intuition with these problems. As we will see in the next section, and in later sections, our intuition can lead us astray in these problems if we aren’t careful.
- So, let’s work this one by the book. We will need to use Theorem 2 on this problem. To this, we’ll first need to compute,

- Therefore, since the limit of the sequence terms with absolute value bars on them goes to zero we know by Theorem 2 that,
 which also means that the sequence converges to a value of zero.
which also means that the sequence converges to a value of zero.
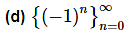
Solution. For this theorem note that all we need to do is realize that this is the sequence in Theorem 3 above using r=−1. So, by Theorem 3 this sequence diverges.
Warning - We now need to give a warning about misusing Theorem 2. Theorem 2 only works if the limit is zero. If the limit of the absolute value of the sequence terms is not zero then the theorem will not hold. The last part of the previous example is a good example of this (and in fact, this warning is the whole reason that part is there). Notice that
and yet,
doesn’t even exist let alone equal 1. So, be careful using this Theorem 2. You must always remember that it only works if the limit is zero.
Before moving on to the next section we need to give one more theorem that we’ll need for proof down the road.
Theorem 4
For the sequence {an} if both  and
and  then {an} is convergent and
then {an} is convergent and 
Proof of Theorem 4
Let ε>0.
Then since 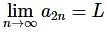 there is an N1>0 such that if n>N1 we know that,
there is an N1>0 such that if n>N1 we know that,
Likewise, because 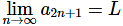 there is an N2>0 such that if n>N2 we know that,
there is an N2>0 such that if n>N2 we know that,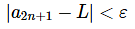
Now, let 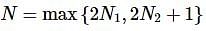 and let n>N. Then either an=a2k for some k>N1 or an=a2k+1 for some k>N2 and so in either case we have that,
and let n>N. Then either an=a2k for some k>N1 or an=a2k+1 for some k>N2 and so in either case we have that,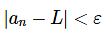
Therefore, 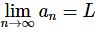 and so {an} convergent.
and so {an} convergent.
More On Sequences
In the previous section, we introduced the concept of a sequence and talked about the limits of sequences and the idea of convergence and divergence for a sequence. In this section we want to take a quick look at some ideas involving sequences. Let’s start off with some terminology and definitions.
Given any sequence {an} we have the following.
1. We call the sequence increasing if an<an+1 for every n.
2. We call the sequence decreasing if an>an+1 for every n.
3. If {an} is an increasing sequence or {an} is a decreasing sequence we call it monotonic.
4. If there exist a number m such that m≤an for every n we say the sequence is bounded below. The number m is sometimes called a lower bound for the sequence.
5. If there exists a number M such that an≤M for every n we say the sequence is bounded above. The number M is sometimes called an upper bound for the sequence.
Note that in order for a sequence to be increasing or decreasing it must be increasing/decreasing for every n. In other words, a sequence that increases for three terms and then decreases for the rest of the terms is NOT a decreasing sequence! Also, note that a monotonic sequence must always increase or it must always decrease.

Bounds of a Sequence
Before moving on we should make a quick point about the bounds of a sequence that is bounded above and/or below. We’ll make the point about lower bounds, but we could just as easily make it about upper bounds.
A sequence is bounded below if we can find any number m such that m≤an for every n.
- Note however that if we find one number m to use for a lower bound then any number smaller than m will also be a lower bound.
- Also, just because we find one lower bound that doesn’t mean there won’t be a “better” lower bound for the sequence than the one we found.
- In other words, there are an infinite number of lower bounds for a sequence that is bounded below, some will be better than others.
Let’s take a look at a couple of examples.
Example 1: Determine if the following sequences are monotonic and/or bounded.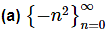
- This sequence is a decreasing sequence (and hence monotonic) because,
 for every n.
for every n. - Also, since the sequence terms will be either zero or negative, this sequence is bounded above.
- We can use any positive number or zero as the bound, M, however, it’s standard to choose the smallest possible bound if we can and it’s a nice number. So, we’ll choose M=0 since, −n2≤0 for every n.
- This sequence is not bounded below, however, since we can always get below any potential bound by taking n large enough. Therefore, while the sequence is bounded above it is not bounded.
- As a side note, we can also note that this sequence diverges (to −∞ if we want to be specific).
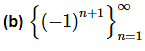
The sequence terms in this sequence alternate between 1 and -1 and so the sequence is neither an increasing sequence nor a decreasing sequence. Since the sequence is neither an increasing nor decreasing sequence it is not a monotonic sequence.
The sequence is bounded, however, since it is bounded above by 1 and bounded below by -1.
Again, we can note that this sequence is also divergent.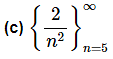
This sequence is a decreasing sequence (and hence monotonic) since,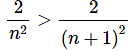
The terms in this sequence are all positive and so it is bounded below by zero. Also, since the sequence is a decreasing sequence the first sequence term will be the largest and so we can see that the sequence will also be bounded above by 2/25. Therefore, this sequence is bounded.
We can also take a quick limit and note that this sequence converges and its limit is zero.
Now, let’s work on a couple more examples that are designed to make sure that we don’t get too used to relying on our intuition with these problems. As we noted in the previous section our intuition can often lead us astray with some of the concepts we’ll be looking at in this chapter.
Example 2: Determine if the following sequences are monotonic and/or bounded.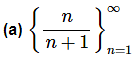
We’ll start with the bounded part of this example first and then come back and deal with the increasing/decreasing question since that is where students often make mistakes with this type of sequence.
- First, n is positive and so the sequence terms are all positive. The sequence is therefore bounded below by zero.
- Likewise, each sequence term is the quotient of a number divided by a larger number and so is guaranteed to be less than one. The sequence is then bounded above by one. So, this sequence is bounded.
Now let’s think about the monotonic question.
- First, students will often make the mistake of assuming that because the denominator is larger the quotient must be decreasing. This will not always be the case and in this case, we would be wrong. This sequence is increasing as we’ll see.
- To determine the increasing/decreasing nature of this sequence we will need to resort to Calculus I techniques. First, consider the following function and its derivative.

- We can see that the first derivative is always positive and so from Calculus I, we know that the function must then be an increasing function. So, how does this help us? Notice that,

- Therefore because n<n+1 and f(x) is increasing we can also say that,

- In other words, the sequence must be increasing.
- Note that now that we know the sequence is an increasing sequence we can get a better lower bound for the sequence.
- Since the sequence is increasing the first term in the sequence must be the smallest term and so since we are starting at n=1 we could also use a lower bound of 1/2 for this sequence.
- It is important to remember that any number that is always less than or equal to all the sequence terms can be a lower bound.
- Some are better than others, however. A quick limit will also tell us that this sequence converges with a limit of 1.
Before moving on to the next part there is a natural question that many students will have at this point.
Ques: Why did we use Calculus to determine the increasing/decreasing nature of the sequence when we could have just plugged in a couple of n’s and quickly determined the same thing?
The answer to this question is the next part of this example!
This is a messy-looking sequence, but it needs to be in order to make the point of this part.
- First, notice that, as with the previous part, the sequence terms are all positive and will all be less than one (since the numerator is guaranteed to be less than the denominator) and so the sequence is bounded.
- Now, let’s move on to the increasing/decreasing question. As with the last problem, many students will look at the exponents in the numerator and denominator and determine based on that sequence terms must decrease.
- This, however, isn’t a decreasing sequence. Let’s take a look at the first few terms to see this.

- The first 10 terms of this sequence are all increasing and so clearly the sequence can’t be a decreasing sequence.
- Recall that a sequence can only be decreasing if ALL the terms are decreasing.
- Now, we can’t make another common mistake and assume that because the first few terms increase then whole sequence must also increase. If we did that we would also be mistaken as this is also not an increasing sequence.
- This sequence is neither decreasing nor increasing. The only sure way to see this is to do the Calculus I approach to increasing/decreasing functions.
- In this case, we’ll need the following function and its derivative.

- This function will have the following three critical points,

- Remember these are the only places where the derivative may change sign!
- Our sequence starts at n=0 and so we can ignore the third one since it lies outside the values of n that we’re considering.
- By plugging in some test values of x we can quickly determine that the derivative is positive for
 and so the function is increasing in this range.
and so the function is increasing in this range. - Likewise, we can see that the derivative is negative for
 and so the function will be decreasing in this range.
and so the function will be decreasing in this range. - So, our sequence will be increasing for 0≤n≤13 and decreasing for n≥13. Therefore, the function is not monotonic.
- Finally, note that this sequence will also converge and has a limit of zero.

Note - So, as the last example has shown we need to be careful in making assumptions about sequences. Our intuition will often not be sufficient to get the correct answer and we can NEVER make assumptions about a sequence based on the value of the first few terms. As the last part has shown there are sequences which will increase or decrease for a few terms and then change direction after that.
- Note as well that we said “first few terms” here, but it is completely possible for a sequence to decrease for the first 10,000 terms and then start increasing for the remaining terms.
- In other words, there is no “magical” value of n for which all we have to do is check up to that point and then we’ll know what the whole sequence will do.
- The only time that we’ll be able to avoid using Calculus I techniques to determine the increasing/decreasing nature of a sequence is in sequences like part (c) of Example 1.
- In this case, increasing n only changed (in fact increased) the denominator and so we were able to determine the behaviour of the sequence based on that.
- In Example 2 however, increasing n increased both the denominator and the numerator.
- In cases like this, there is no way to determine which increase will “win out” and cause the sequence terms to increase or decrease and so we need to resort to Calculus I techniques to answer the question.
We’ll close out this section with a nice theorem that we’ll use in some of the proofs later in this chapter.
Theorem
If {an} is bounded and monotonic then {an} is convergent.
Be careful to not misuse this theorem. It does not say that if a sequence is not bounded and/or not monotonic that it is divergent. Example 2b is a good case in point. The sequence in that example was not monotonic but it does converge.
Note as well that we can make several variants of this theorem. If {an} is bounded above and increasing then it converges and likewise if {an} is bounded below and decreasing then it converges.
|
161 videos|58 docs
|
FAQs on Basics of Sequence - Algebra - Mathematics
| 1. What is a sequence in mathematics? |  |
| 2. What are the basics of sequence mathematics? |  |
| 3. How can sequences be used in real-life situations? |  |
| 4. What are arithmetic and geometric sequences? |  |
| 5. What are some common applications of sequence mathematics? |  |

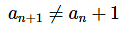 , so be very careful when writing subscripts to make sure that the “+1” doesn’t migrate out of the subscript! This is an easy mistake to make when you first start dealing with this kind of thing.
, so be very careful when writing subscripts to make sure that the “+1” doesn’t migrate out of the subscript! This is an easy mistake to make when you first start dealing with this kind of thing.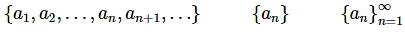

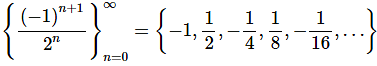


 exists and is finite we say that the sequence is convergent.
exists and is finite we say that the sequence is convergent.  doesn’t exist or is infinite we say the sequence diverges.
doesn’t exist or is infinite we say the sequence diverges.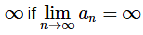 and if
and if  we will sometimes say that the sequence diverges to −∞.
we will sometimes say that the sequence diverges to −∞.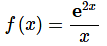 and note that,
and note that,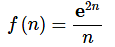 .
. So, the sequence in this part diverges (to ∞).
So, the sequence in this part diverges (to ∞).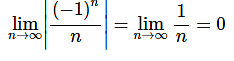
 which also means that the sequence converges to a value of zero.
which also means that the sequence converges to a value of zero.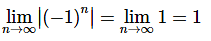 and yet,
and yet,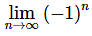 doesn’t even exist let alone equal 1. So, be careful using this Theorem 2. You must always remember that it only works if the limit is zero.
doesn’t even exist let alone equal 1. So, be careful using this Theorem 2. You must always remember that it only works if the limit is zero. for every n.
for every n.



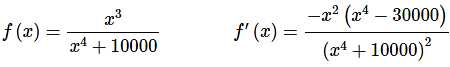
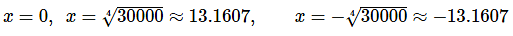
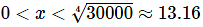 and so the function is increasing in this range.
and so the function is increasing in this range. 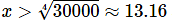 and so the function will be decreasing in this range.
and so the function will be decreasing in this range.



















