Bayes' Theorem of Probability | Mathematics for ACT PDF Download

Introduction 

Bayes theorem is a theorem in probability and statistics, named after the Reverend Thomas Bayes, that helps in determining the probability of an event that is based on some event that has already occurred. Bayes theorem has many applications such as bayesian interference, in the healthcare sector - to determine the chances of developing health problems with an increase in age and many others. Here, we will aim at understanding the use of the Bayes theorem in determining the probability of events, its statement, formula, and derivation with the help of examples.

What is Bayes Theorem?

Bayes theorem, in simple words, determines the conditional probability of an event A given that event B has already occurred. Bayes theorem is also known as the Bayes Rule or Bayes Law. It is a method to determine the probability of an event based on the occurrences of prior events. It is used to calculate conditional probability. Bayes theorem calculates the probability based on the hypothesis. Now, let us state the theorem and its proof. Bayes theorem states that the conditional probability of an event A, given the occurrence of another event B, is equal to the product of the likelihood of B, given A and the probability of A. It is given as: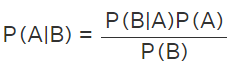

• Here, P(A) = how likely A happens(Prior knowledge)- The probability of a hypothesis is true before any evidence is present.
• P(B) = how likely B happens(Marginalization)- The probability of observing the evidence.
• P(A/B) = how likely A happens given that B has happened(Posterior)-The probability of a hypothesis is true given the evidence.
• P(B/A) = how likely B happens given that A has happened(Likelihood)- The probability of seeing the evidence if the hypothesis is true.

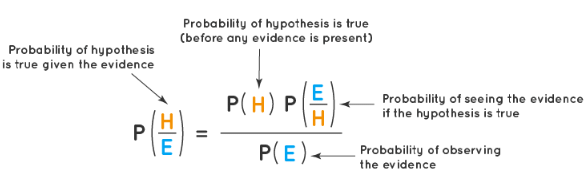
Bayes Theorem - Statement

The statement of Bayes Theorem is as follows: Let E₁,E₂,E₃,...,E_n be a set of events associated with a sample space S, where all events E₁,E₂,E₃,...,E_n have non-zero probability of occurrence and they form a partition of S. Let A be any event which occurs with E₁ or E₂ or E₃... or E_n then according to Bayes Theorem,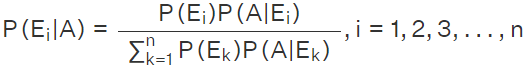

• Here Eii ∩ Ejj = φ, where i ≠ j. (i.e) They are mutually exhaustive events
• The union of all the events of the partition, should give the sample space.
• 0 ≤ P(Eii) ≤ 1

Proof of Bayes Theorem

To prove the Bayes Theorem, we will use the total probability and conditional probability formulas. The total probability of an event A is calculated when not enough data is known about event A, then we use other events related to event A to determine its probability. Conditional probability is the probability of event A given that other related events have already occurred.
(Eii), be is a partition of the sample space S. Let A be an event that occurred. Let us express A in terms of (Eii). 
A = A ∩ S
= A ∩ (E1,E2,E3,...,EnE1,E2,E3,...,En)
A = (A ∩E1E1) ∪ (A ∩E1E1) ∪ (A ∩E1E1)....∪ ( A ∩E1E1)
P(A) = P[(A ∩ E1E1) ∪ (A ∩E1E1) ∪ (A ∩E1E1)....∪ ( A ∩E1E1)]
We know that when A and B are disjoint sets, then P(A∪B) = P(A) + P(B)
Thus here, P(A) = P(A ∩E1E1) +P(A ∩E1E1)+ P(A ∩E1E1).....P(A ∩EnEn)
According to the multiplication theorem of a dependent event, we have
P(A) = P(E). P(A/E1E1) + P(E). P(A/E2E2) + P(E). P(A/E3E3)......+ P(A/EnEn)
Thus total probability of P(A) = 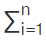 P(Ei)P(A|Ei),i=1,2,3,...,n∑i=1nP(Ei)P(A|Ei),i=1,2,3,...,n --- (1) 
Recalling the conditional probability, we get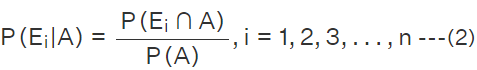 
Using the formula for conditional probability of P(A|Ei)P(A|Ei), we have 
P(Ei∩A)=P(A|Ei)P(Ei)P(Ei∩A)=P(A|Ei)P(Ei) --- (3) 
Substituting equations (1) and (3) in equation (2), we get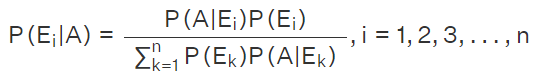 
Hence, Bayes Theorem is proved.

Bayes Theorem Formula 

Bayes theorem formula exists for events and random variables. Bayes Theorem formulas are derived from the definition of conditional probability. It can be derived for events A and B, as well as continuous random variables X and Y. Let us first see the formula for events.

Bayes Theorem Formula for Events
The formula for events derived from the definition of conditional probability is: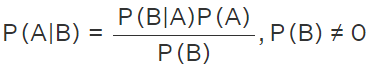

Derivation:
According to the definition of conditional probability,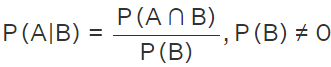
 and we know that

P(A∩B)=P(B∩A)=P(B|A)P(A) , which implies,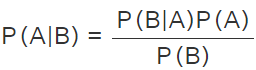
Hence, the Bayes theorem formula for events is derived.

Bayes Theorem for Continuous Random Variables

The formula for continuous random variables X and Y derived from the definition of the conditional probability of continuous variables is: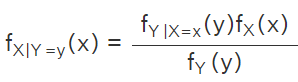

Derivation:
According to the definition of conditional density or conditional probability of continuous random variables, we know that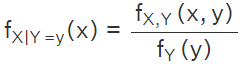
 and 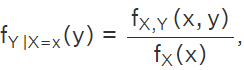 which implies,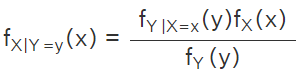

Hence, the Bayes Theorem formula for random continuous variables is derived.

Difference Between Conditional Probability and Bayes Theorem

Terms Related to Bayes Theorem

As we have studied about Bayes theorem in detail, let us understand the meanings of a few terms related to the concept which have been used in the Bayes theorem formula and derivation:

• Conditional Probability: Conditional Probability is the probability of an event A based on the occurrence of another event B. It is denoted by P(A|B) and represents the probability of A given that event B has already happened.
• Joint Probability - Joint probability measures the probability of two more events occurring together and at the same time. For two events A and B, it is denoted by P(A∩B).
• Random Variables: Random variable is a real-valued variable whose possible values are determined by a random experiment. The probability of such variables is also called the experimental probability.
• Posterior Probability: Posterior probability is the probability of an event that is calculated after all the information related to the event has been accounted for. It is also known as conditional probability.
• Prior Probability: Prior probability is the probability of an event that is calculated before considering the new information obtained. It is the probability of an outcome that is determined based on current knowledge before the experiment is performed.