Binary Heap & Heapsort | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download

Binary Heap

A Binary Heap is a Binary Tree with following properties.

1) It’s a complete tree (All levels are completely filled except possibly the last level and the last level has all keys as left as possible). This property of Binary Heap makes them suitable to be stored in an array.
2) A Binary Heap is either Min Heap or Max Heap. In a Min Binary Heap, the key at root must be minimum among all keys present in Binary Heap. The same property must be recursively true for all nodes in Binary Tree. Max Binary Heap is similar to MinHeap.
Examples of Min Heap:
            10                      10
         /      \               /       \
       20        100          15         30
      /                      /  \        /  \
    30                     40    50    100   40

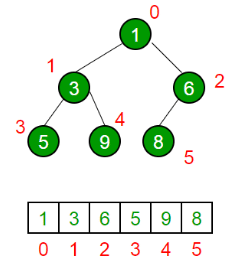
How is Binary Heap represented?
A Binary Heap is a Complete Binary Tree. A binary heap is typically represented as an array.

• The root element will be at Arr[0].
• Below table shows indexes of other nodes for the ith node, i.e., Arr[i]:

Arr[(i-1)/2]    Returns the parent node

Arr[(2*i)+1]    Returns the left child node

Arr[(2*i)+2]    Returns the right child node

traversal method use to achieve Array representation is Level Order

Applications of Heaps:

(1) Heap Sort: Heap Sort uses Binary Heap to sort an array in O(nLogn) time.
(2) Priority Queue: Priority queues can be efficiently implemented using Binary Heap because it supports insert(), delete() and extractmax(), decreaseKey() operations in O(logn) time. Binomoial Heap and Fibonacci Heap are variations of Binary Heap. These variations perform union also efficiently.
(3) Graph Algorithms: The priority queues are especially used in Graph Algorithms like Dijkstra’s Shortest Path and Prim’s Minimum Spanning Tree.
(4) Many problems can be efficiently solved using Heaps. See following for example.

(a) K’th Largest Element in an array.

(b) Sort an almost sorted array/

(c) Merge K Sorted Arrays.

Operations on Min Heap:

(1) getMini(): It returns the root element of Min Heap. Time Complexity of this operation is O(1).
(2) extractMin(): Removes the minimum element from MinHeap. Time Complexity of this Operation is O(Logn) as this operation needs to maintain the heap property (by calling heapify()) after removing root.
(3) decreaseKey(): Decreases value of key. The time complexity of this operation is O(Logn). If the decreases key value of a node is greater than the parent of the node, then we don’t need to do anything. Otherwise, we need to traverse up to fix the violated heap property.
(4) insert(): Inserting a new key takes O(Logn) time. We add a new key at the end of the tree. IF new key is greater than its parent, then we don’t need to do anything. Otherwise, we need to traverse up to fix the violated heap property.
(5) delete(): Deleting a key also takes O(Logn) time. We replace the key to be deleted with minum infinite by calling decreaseKey(). After decreaseKey(), the minus infinite value must reach root, so we call extractMin() to remove the key.
Below is the implementation of basic heap operations.
C++
// A C++ program to demonstrate common Binary Heap Operations
#include<iostream>
#include<climits>
using namespace std;
// Prototype of a utility function to swap two integers
void swap(int *x, int *y);
// A class for Min Heap
class MinHeap
{
    int *harr; // pointer to array of elements in heap
    int capacity; // maximum possible size of min heap
    int heap_size; // Current number of elements in min heap
public:
    // Constructor
    MinHeap(int capacity);
    // to heapify a subtree with the root at given index
    void MinHeapify(int );
    int parent(int i) { return (i-1)/2; }
    // to get index of left child of node at index i
    int left(int i) { return (2*i + 1); }
    // to get index of right child of node at index i
    int right(int i) { return (2*i + 2); }
    // to extract the root which is the minimum element
    int extractMin();
    // Decreases key value of key at index i to new_val
    void decreaseKey(int i, int new_val);
    // Returns the minimum key (key at root) from min heap
    int getMin() { return harr[0]; }
    // Deletes a key stored at index i
    void deleteKey(int i);
    // Inserts a new key 'k'
    void insertKey(int k);
};
// Constructor: Builds a heap from a given array a[] of given size
MinHeap::MinHeap(int cap)
{
    heap_size = 0;
    capacity = cap;
    harr = new int[cap];
}
// Inserts a new key 'k'
void MinHeap::insertKey(int k)
{
    if (heap_size == capacity)
    {
        cout << "\nOverflow: Could not insertKey\n";
        return;
    }
    // First insert the new key at the end
    heap_size++;
    int i = heap_size - 1;
    harr[i] = k;
    // Fix the min heap property if it is violated
    while (i != 0 && harr[parent(i)] > harr[i])
    {
       swap(&harr[i], &harr[parent(i)]);
       i = parent(i);
    }
}
// Decreases value of key at index 'i' to new_val.  It is assumed that
// new_val is smaller than harr[i].
void MinHeap::decreaseKey(int i, int new_val)
{
    harr[i] = new_val;
    while (i != 0 && harr[parent(i)] > harr[i])
    {
       swap(&harr[i], &harr[parent(i)]);
       i = parent(i);
    }
}
// Method to remove minimum element (or root) from min heap
int MinHeap::extractMin()
{
    if (heap_size <= 0)
        return INT_MAX;
    if (heap_size == 1)
    {
        heap_size--;
        return harr[0];
    }
    // Store the minimum value, and remove it from heap
    int root = harr[0];
    harr[0] = harr[heap_size-1];
    heap_size--;
    MinHeapify(0);
    return root;
}
// This function deletes key at index i. It first reduced value to minus
// infinite, then calls extractMin()
void MinHeap::deleteKey(int i)
{
    decreaseKey(i, INT_MIN);
    extractMin();
}
// A recursive method to heapify a subtree with the root at given index
// This method assumes that the subtrees are already heapified
void MinHeap::MinHeapify(int i)
{
    int l = left(i);
    int r = right(i);
    int smallest = i;
    if (l < heap_size && harr[l] < harr[i])
        smallest = l;
    if (r < heap_size && harr[r] < harr[smallest])
        smallest = r;
    if (smallest != i)
    {
        swap(&harr[i], &harr[smallest]);
        MinHeapify(smallest);
    }
}

// A utility function to swap two elements
void swap(int *x, int *y)
{
    int temp = *x;
    *x = *y;
    *y = temp;
}
// Driver program to test above functions
int main()
{
    MinHeap h(11);
    h.insertKey(3);
    h.insertKey(2);
    h.deleteKey(1);
    h.insertKey(15);
    h.insertKey(5);
    h.insertKey(4);
    h.insertKey(45);
    cout << h.extractMin() << " ";
    cout << h.getMin() << " ";
    h.decreaseKey(2, 1);
    cout << h.getMin();
    return 0;
}

Python
# A Python program to demonstrate common binary heap operations
# Import the heap functions from python library
from heapq import heappush, heappop, heapify
# heappop - pop and return the smallest element from heap
# heappush - push the value item onto the heap, maintaining
#             heap invarient
# heapify - transform list into heap, in place, in linear time
# A class for Min Heap
class MinHeap:
    # Constructor to initialize a heap
    def __init__(self):
        self.heap = []
    def parent(self, i):
        return (i-1)/2
    # Inserts a new key 'k'
    def insertKey(self, k):
        heappush(self.heap, k)
    # Decrease value of key at index 'i' to new_val
    # It is assumed that new_val is smaller than heap[i]
    def decreaseKey(self, i, new_val):
        self.heap[i]  = new_val
        while(i != 0 and self.heap[self.parent(i)] > self.heap[i]):
            # Swap heap[i] with heap[parent(i)]
            self.heap[i] , self.heap[self.parent(i)] = (
            self.heap[self.parent(i)], self.heap[i])
    # Method to remove minium element from min heap
    def extractMin(self):
        return heappop(self.heap)
    # This functon deletes key at index i. It first reduces
    # value to minus infinite and then calls extractMin()
    def deleteKey(self, i):
        self.decreaseKey(i, float("-inf"))
        self.extractMin()
   # Get the minimum element from the heap
   def getMin(self):
       return self.heap[0]
# Driver pgoratm to test above function
heapObj = MinHeap()
heapObj.insertKey(3)
heapObj.insertKey(2)
heapObj.deleteKey(1)
heapObj.insertKey(15)
heapObj.insertKey(5)
heapObj.insertKey(4)
heapObj.insertKey(45)
print heapObj.extractMin(),
print heapObj.getMin(),
heapObj.decreaseKey(2, 1)
print heapObj.getMin()
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)

C#

// C# program to demonstrate common
// Binary Heap Operations - Min Heap
using System;
// A class for Min Heap
class MinHeap{
// To store array of elements in heap
public int[] heapArray{ get; set; }
// max size of the heap
public int capacity{ get; set; }
// Current number of elements in the heap
public int current_heap_size{ get; set; }
// Constructor
public MinHeap(int n)
{
    capacity = n;
    heapArray = new int[capacity];
    current_heap_size = 0;
}
// Swapping using reference
public static void Swap<T>(ref T lhs, ref T rhs)
{
    T temp = lhs;
    lhs = rhs;
    rhs = temp;
}
// Get the Parent index for the given index
public int Parent(int key)
{
    return (key - 1) / 2;
}
// Get the Left Child index for the given index
public int Left(int key)
{
    return 2 * key + 1;
}
// Get the Right Child index for the given index
public int Right(int key)
{
    return 2 * key + 2;
}
// Inserts a new key
public bool insertKey(int key)
    if (current_heap_size == capacity)
    {
        // heap is full
        return false;
    }
    // First insert the new key at the end
    int i = current_heap_size;
    heapArray[i] = key;
    current_heap_size++;
    // Fix the min heap property if it is violated
    while (i != 0 && heapArray[i] <

                     heapArray[Parent(i)])
    {
        Swap(ref heapArray[i],
             ref heapArray[Parent(i)]);
        i = Parent(i);
    }
    return true;
}
// Decreases value of given key to new_val.
// It is assumed that new_val is smaller
// than heapArray[key].
public void decreaseKey(int key, int new_val)
{
    heapArray[key] = new_val;
    while (key != 0 && heapArray[key] <
                       heapArray[Parent(key)])
    {
        Swap(ref heapArray[key],
             ref heapArray[Parent(key)]);
        key = Parent(key);
    }
}
// Returns the minimum key (key at
// root) from min heap
public int getMin()
{
    return heapArray[0];
}
// Method to remove minimum element
// (or root) from min heap
public int extractMin()
{
    if (current_heap_size <= 0)
    {
        return int.MaxValue;
    }
    if (current_heap_size == 1)
    {
        current_heap_size--;
        return heapArray[0];
    }
    // Store the minimum value,
    // and remove it from heap
    int root = heapArray[0];
    heapArray[0] = heapArray[current_heap_size - 1];
    current_heap_size--;
    MinHeapify(0);
    return root;
}
// This function deletes key at the
// given index. It first reduced value
// to minus infinite, then calls extractMin()
public void deleteKey(int key)
{
    decreaseKey(key, int.MinValue);
    extractMin();
}
// A recursive method to heapify a subtree
// with the root at given index
// This method assumes that the subtrees
// are already heapified
public void MinHeapify(int key)
{
    int l = Left(key);
    int r = Right(key);
    int smallest = key;
    if (l < current_heap_size &&
        heapArray[l] < heapArray[smallest])
    {
        smallest = l;
    }
    if (r < current_heap_size &&
        heapArray[r] < heapArray[smallest])
    {
        smallest = r;
    }
    if (smallest != key)
    {
        Swap(ref heapArray[key],
             ref heapArray[smallest]);
        MinHeapify(smallest);
    }
}
  // Increases value of given key to new_val.
// It is assumed that new_val is greater
// than heapArray[key].
// Heapify from the given key
public void increaseKey(int key, int new_val)
{
    heapArray[key] = new_val;
    MinHeapify(key);
}
// Changes value on a key
public void changeValueOnAKey(int key, int new_val)
{
    if (heapArray[key] == new_val)
    {
        return;
    }
    if (heapArray[key] < new_val)
    {
        increaseKey(key, new_val);
    } else
    {
        decreaseKey(key, new_val);
    }
}
}
static class MinHeapTest{
// Driver code
public static void Main(string[] args)
{
    MinHeap h = new MinHeap(11);
    h.insertKey(3);
    h.insertKey(2);
    h.deleteKey(1);
    h.insertKey(15);
    h.insertKey(5);
    h.insertKey(4);
    h.insertKey(45);
    Console.Write(h.extractMin() + " ");
    Console.Write(h.getMin() + " ");
    h.decreaseKey(2, 1);
    Console.Write(h.getMin());
}
}
// This code is contributed by
// Dinesh Clinton Albert(dineshclinton)

Output:
2 4 1

HeapSort

Heap sort is a comparison-based sorting technique based on Binary Heap data structure. It is similar to selection sort where we first find the minimum element and place the minimum element at the beginning. We repeat the same process for the remaining elements.

What is Binary Heap?
Let us first define a Complete Binary Tree. A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible
A Binary Heap is a Complete Binary Tree where items are stored in a special order such that the value in a parent node is greater(or smaller) than the values in its two children nodes. The former is called max heap and the latter is called min-heap. The heap can be represented by a binary tree or array.

Why array based representation for Binary Heap? 

Since a Binary Heap is a Complete Binary Tree, it can be easily represented as an array and the array-based representation is space-efficient. If the parent node is stored at index I, the left child can be calculated by 2 * I + 1 and the right child by 2 * I + 2 (assuming the indexing starts at 0).

Heap Sort Algorithm for sorting in increasing order:
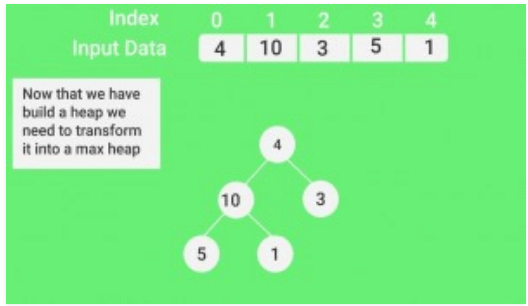
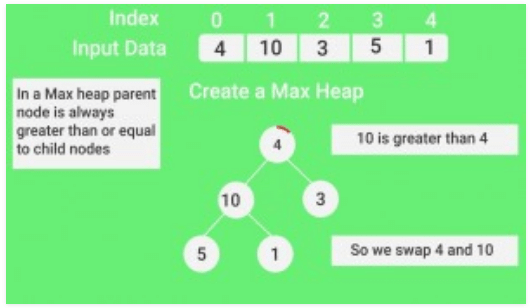
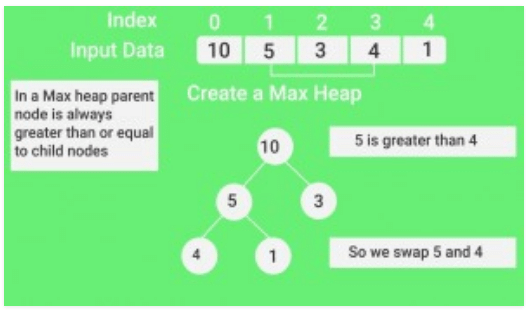
1. Build a max heap from the input data.
2. At this point, the largest item is stored at the root of the heap. Replace it with the last item of the heap followed by reducing the size of heap by 1. Finally, heapify the root of the tree.
3. Repeat step 2 while the size of the heap is greater than 1.

How to build the heap?
Heapify procedure can be applied to a node only if its children nodes are heapified. So the heapification must be performed in the bottom-up order.

Lets understand with the help of an example:
Input data: 4, 10, 3, 5, 1
         4(0)
        /   \
     10(1)   3(2)
    /   \
 5(3)    1(4)

The numbers in bracket represent the indices in the array
representation of data.

Applying heapify procedure to index 1:
         4(0)
        /   \
    10(1)    3(2)
    /   \
5(3)    1(4)

Applying heapify procedure to index 0:
        10(0)
        /  \
     5(1)  3(2)
    /   \
 4(3)    1(4)
The heapify procedure calls itself recursively to build heap

 in top down manner.

C++
// C++ program for implementation of Heap Sort
#include <iostream>
using namespace std;
// To heapify a subtree rooted with node i which is
// an index in arr[]. n is size of heap
void heapify(int arr[], int n, int i)
{
    int largest = i; // Initialize largest as root
    int l = 2 * i + 1; // left = 2*i + 1
    int r = 2 * i + 2; // right = 2*i + 2
    // If left child is larger than root
    if (l < n && arr[l] > arr[largest])
        largest = l;
    // If right child is larger than largest so far
    if (r < n && arr[r] > arr[largest])
        largest = r;
    // If largest is not root
    if (largest != i) {
        swap(arr[i], arr[largest]);
        // Recursively heapify the affected sub-tree
        heapify(arr, n, largest);
    }
}
// main function to do heap sort
void heapSort(int arr[], int n)
{
    // Build heap (rearrange array)
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);
    // One by one extract an element from heap
    for (int i = n - 1; i > 0; i--) {
        // Move current root to end
        swap(arr[0], arr[i]);
        // call max heapify on the reduced heap
        heapify(arr, i, 0);
    }
}
/* A utility function to print array of size n */
void printArray(int arr[], int n)
{
    for (int i = 0; i < n; ++i)
        cout << arr[i] << " ";
    cout << "\n";
}
// Driver code
int main()
{
    int arr[] = { 12, 11, 13, 5, 6, 7 };
    int n = sizeof(arr) / sizeof(arr[0]);
    heapSort(arr, n);
    cout << "Sorted array is \n";
    printArray(arr, n);
}

Java
// Java program for implementation of Heap Sort
public class HeapSort {
    public void sort(int arr[])
    {
        int n = arr.length;
        // Build heap (rearrange array)
        for (int i = n / 2 - 1; i >= 0; i--)
            heapify(arr, n, i);
        // One by one extract an element from heap
        for (int i = n - 1; i > 0; i--) {
            // Move current root to end
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
            // call max heapify on the reduced heap
            heapify(arr, i, 0);
        }
    }
    // To heapify a subtree rooted with node i which is
    // an index in arr[]. n is size of heap
    void heapify(int arr[], int n, int i)
    {
        int largest = i; // Initialize largest as root
        int l = 2 * i + 1; // left = 2*i + 1
        int r = 2 * i + 2; // right = 2*i + 2
        // If left child is larger than root
        if (l < n && arr[l] > arr[largest])
            largest = l;
        // If right child is larger than largest so far
        if (r < n && arr[r] > arr[largest])
            largest = r;
        // If largest is not root
        if (largest != i) {
            int swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;
            // Recursively heapify the affected sub-tree
            heapify(arr, n, largest);
        }
    }
    /* A utility function to print array of size n */
    static void printArray(int arr[])
    {
        int n = arr.length;
        for (int i = 0; i < n; ++i)
            System.out.print(arr[i] + " ");
        System.out.println();
    }
    // Driver code
    public static void main(String args[])
    {
        int arr[] = { 12, 11, 13, 5, 6, 7 };
        int n = arr.length;
        HeapSort ob = new HeapSort();
        ob.sort(arr);
        System.out.println("Sorted array is");
        printArray(arr);
    }
}

Python
# Python program for implementation of heap Sort
# To heapify subtree rooted at index i.
# n is size of heap
def heapify(arr, n, i):
    largest = i  # Initialize largest as root
    l = 2 * i + 1     # left = 2*i + 1
    r = 2 * i + 2     # right = 2*i + 2
    # See if left child of root exists and is
    # greater than root
    if l < n and arr[largest] < arr[l]:
        largest = l
    # See if right child of root exists and is
    # greater than root
    if r < n and arr[largest] < arr[r]:
        largest = r
    # Change root, if needed
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]  # swap
        # Heapify the root.
        heapify(arr, n, largest)
# The main function to sort an array of given size
def heapSort(arr):
    n = len(arr)
    # Build a maxheap.
    for i in range(n//2 - 1, -1, -1):
        heapify(arr, n, i)
    # One by one extract elements
    for i in range(n-1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # swap
        heapify(arr, i, 0)
# Driver code
arr = [12, 11, 13, 5, 6, 7]
heapSort(arr)
n = len(arr)
print("Sorted array is")
for i in range(n):
    print("%d" % arr[i]),
# This code is contributed by Mohit Kumra

C#
// C# program for implementation of Heap Sort
using System;
public class HeapSort {
    public void sort(int[] arr)
    {
        int n = arr.Length;
        // Build heap (rearrange array)
        for (int i = n / 2 - 1; i >= 0; i--)
            heapify(arr, n, i);
       // One by one extract an element from heap
        for (int i = n - 1; i > 0; i--) {
            // Move current root to end
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
           // call max heapify on the reduced heap
            heapify(arr, i, 0);
        }
    }
    // To heapify a subtree rooted with node i which is
    // an index in arr[]. n is size of heap
    void heapify(int[] arr, int n, int i)
    {
        int largest = i; // Initialize largest as root
        int l = 2 * i + 1; // left = 2*i + 1
        int r = 2 * i + 2; // right = 2*i + 2
        // If left child is larger than root
        if (l < n && arr[l] > arr[largest])
            largest = l;
        // If right child is larger than largest so far
        if (r < n && arr[r] > arr[largest])
            largest = r;
        // If largest is not root
        if (largest != i) {
            int swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;
            // Recursively heapify the affected sub-tree
            heapify(arr, n, largest);
       }
    }
    /* A utility function to print array of size n */
    static void printArray(int[] arr)
    {
        int n = arr.Length;
        for (int i = 0; i < n; ++i)
            Console.Write(arr[i] + " ");
        Console.Read();
    }
    // Driver code
    public static void Main()
    {
        int[] arr = { 12, 11, 13, 5, 6, 7 };
        int n = arr.Length;
        HeapSort ob = new HeapSort();
        ob.sort(arr);
        Console.WriteLine("Sorted array is");
        printArray(arr);
    }
}
// This code is contributed
// by Akanksha Rai(Abby_akku)

PHP
<?php
// Php program for implementation of Heap Sort
// To heapify a subtree rooted with node i which is
// an index in arr[]. n is size of heap
function heapify(&$arr, $n, $i)
{
    $largest = $i; // Initialize largest as root
    $l = 2*$i + 1; // left = 2*i + 1
    $r = 2*$i + 2; // right = 2*i + 2
    // If left child is larger than root
    if ($l < $n && $arr[$l] > $arr[$largest])
        $largest = $l;
    // If right child is larger than largest so far
    if ($r < $n && $arr[$r] > $arr[$largest])
        $largest = $r;
    // If largest is not root
    if ($largest != $i)
    {
        $swap = $arr[$i];
        $arr[$i] = $arr[$largest];
        $arr[$largest] = $swap;
        // Recursively heapify the affected sub-tree
        heapify($arr, $n, $largest);
    }
}
// main function to do heap sort
function heapSort(&$arr, $n)
{
    // Build heap (rearrange array)
    for ($i = $n / 2 - 1; $i >= 0; $i--)

        heapify($arr, $n, $i);
    // One by one extract an element from heap
    for ($i = $n-1; $i > 0; $i--)
    {
        // Move current root to end
        $temp = $arr[0];
            $arr[0] = $arr[$i];
            $arr[$i] = $temp;
        // call max heapify on the reduced heap
        heapify($arr, $i, 0);
    }
}
/* A utility function to print array of size n */
function printArray(&$arr, $n)
{
    for ($i = 0; $i < $n; ++$i)
        echo ($arr[$i]." ") ;
}
// Driver program
    $arr = array(12, 11, 13, 5, 6, 7);
    $n = sizeof($arr)/sizeof($arr[0]);
    heapSort($arr, $n);
    echo 'Sorted array is ' . "\n";
    printArray($arr , $n);
// This code is contributed by Shivi_Aggarwal
?>

Javascript

<script>
// JavaScript program for implementation
// of Heap Sort
function sort( arr)
    {
        var n = arr.length;
        // Build heap (rearrange array)
        for (var i = n / 2 - 1; i >= 0; i--)
            heapify(arr, n, i);
        // One by one extract an element from heap
        for (var i = n - 1; i > 0; i--) {
            // Move current root to end
            var temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
            // call max heapify on the reduced heap
            heapify(arr, i, 0);
        }
    }
    // To heapify a subtree rooted with node i which is
    // an index in arr[]. n is size of heap
    function heapify(arr, n, i)
    {
        var largest = i; // Initialize largest as root
        var l = 2 * i + 1; // left = 2*i + 1
        var r = 2 * i + 2; // right = 2*i + 2
        // If left child is larger than root
        if (l < n && arr[l] > arr[largest])
            largest = l;

        // If right child is larger than largest so far
        if (r < n && arr[r] > arr[largest])
            largest = r;
        // If largest is not root
        if (largest != i) {
            var swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;
            // Recursively heapify the affected sub-tree
            heapify(arr, n, largest);
        }

    }
    /* A utility function to print array of size n */
    function printArray(arr)
    {
        var n = arr.length;
        for (var i = 0; i < n; ++i)
            document.write(arr[i] + " ");
    }
    var arr = [ 12, 11, 13, 5, 6, 7 ];
    var n = arr.length;
    sort(arr);
    document.write( "Sorted array is <br>");
    printArray(arr, n);
// This code is contributed by SoumikMondal
</script>

Output
Sorted array is
5 6 7 11 12 13

Notes: 
Heap sort is an in-place algorithm.
Its typical implementation is not stable, but can be made stable

Time Complexity: Time complexity of heapify is O(Logn). Time complexity of createAndBuildHeap() is O(n) and the overall time complexity of Heap Sort is O(nLogn).
Applications of HeapSort 

1. Sort a nearly sorted (or K sorted) array 

2. k largest(or smallest) elements in an array 

Heap sort algorithm has limited uses because Quicksort and Mergesort are better in practice. Nevertheless, the Heap data structure itself is enormously used.

Snapshots: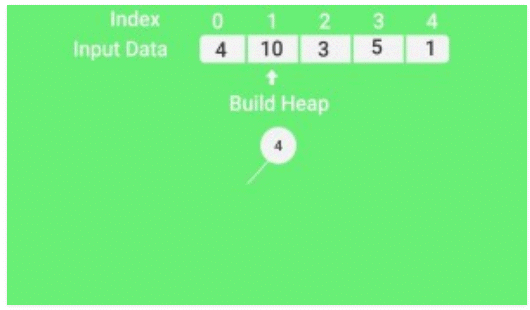
 

Quiz on Heap Sort

Other Sorting Algorithms on GeeksforGeeks/GeeksQuiz:

QuickSort, Selection Sort, Bubble Sort, Insertion Sort, Merge Sort, Heap Sort, QuickSort, Radix Sort, Counting Sort, Bucket Sort, ShellSort, Comb Sort, Pigeonhole Sort