Binary Tree | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download
Introduction
Trees: Unlike Arrays, Linked Lists, Stack and queues, which are linear data structures, trees are hierarchical data structures.
Tree Vocabulary: The topmost node is called root of the tree. The elements that are directly under an element are called its children. The element directly above something is called its parent. For example, ‘a’ is a child of ‘f’, and ‘f’ is the parent of ‘a’. Finally, elements with no children are called leaves.
Why Trees?
- One reason to use trees might be because you want to store information that naturally forms a hierarchy. For example, the file system on a computer:
file system
- Trees (with some ordering e.g., BST) provide moderate access/search (quicker than Linked List and slower than arrays).
- Trees provide moderate insertion/deletion (quicker than Arrays and slower than Unordered Linked Lists).
- Like Linked Lists and unlike Arrays, Trees don’t have an upper limit on number of nodes as nodes are linked using pointers.
Main applications of trees include:
- Manipulate hierarchical data.
- Make information easy to search (see tree traversal).
- Manipulate sorted lists of data.
- As a workflow for compositing digital images for visual effects.
- Router algorithms
- Form of a multi-stage decision-making (see business chess).
Binary Tree: A tree whose elements have at most 2 children is called a binary tree. Since each element in a binary tree can have only 2 children, we typically name them the left and right child.
Binary Tree Representation in C: A tree is represented by a pointer to the topmost node in tree. If the tree is empty, then value of root is NULL.
A Tree node contains following parts:
- Data
- Pointer to left child
- Pointer to right child
In C, we can represent a tree node using structures. Below is an example of a tree node with an integer data.
- C++

- Python

- Java

- C#

- Javascript

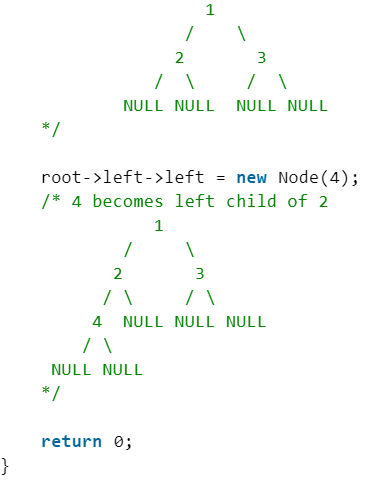
First Simple Tree in C
Let us create a simple tree with 4 nodes in C. The created tree would be as following.
- C++


- C



- Python


- Java



- C#



Summary: Tree is a hierarchical data structure. Main uses of trees include maintaining hierarchical data, providing moderate access and insert/delete operations. Binary trees are special cases of tree where every node has at most two children.
Binary Tree Properties
Maximum Nodes at Level 'l' in a Binary Tree:
- Formula: 2l
- Proof by induction:
- For root l = 0, nodes = (20 = 1)
- Assume maximum nodes at level l is 2l
- Since every node has at most 2 children, the next level would have 2*2l = 2l+1 nodes
Maximum Number of Nodes in a Binary Tree of Height 'h':
- Formula: 2h-1
- Derivation:
- A tree has maximum nodes if all levels have maximum nodes.
- The sum of a geometric series with h terms is (2h+1- 1).
Minimum Possible Height in a Binary Tree with N Nodes:
- Formula: (log2(N+1) - 1)
- Derived from the fact that the minimum possible height is when all levels have maximum nodes.
Minimum Number of Levels in a Binary Tree with L Leaves:
- Formula: (log2(L)+ 1)
- The minimum number of levels is achieved when all leaves are at the same level.
Relationship Between Leaf Nodes (L) and Internal Nodes with Two Children (T):
- In Binary tree where every node has 0 or 2 children, the number of leaf nodes is always one more than nodes with two children.
- Formula: (L = T + 1)
- Proof:
- No. of leaf nodes (L) i.e. total elements present at the bottom of tree =
2h-1 (h is height of tree)
No. of internal nodes = {total no. of nodes} - {leaf nodes} =
{ 2h - 1 } - {2h-1} = 2h-1 (2-1) - 1 = 2h-1 - 1
So , L = 2h-1
T = 2h-1 - 1
Therefore L = T + 1
- No. of leaf nodes (L) i.e. total elements present at the bottom of tree =
|
119 docs|30 tests
|
FAQs on Binary Tree - Programming and Data Structures - Computer Science Engineering (CSE)
| 1. What is a binary tree? |  |
| 2. What are the properties of a binary tree? |  |
| 3. How do binary trees differ from other tree data structures? |  |
| 4. What is the time complexity of searching for a specific element in a binary tree? |  |
| 5. Can a binary tree have duplicate values? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|