Binomial Distribution | Business Mathematics and Statistics - B Com PDF Download
The Binomial Probability Distribution
A binomial experiment is one that possesses the following properties:
- The experiment consists of n repeated trials;
- Each trial results in an outcome that may be classified as a success or a failure (hence the name, binomial);
- The probability of a success, denoted by p, remains constant from trial to trial and repeated trials are independent.
The number of successes X in n trials of a binomial experiment is called a binomial random variable.
The probability distribution of the random variable X is called a binomial distribution, and is given by the formula: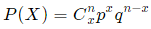
where
n = the number of trials
x = 0, 1, 2, ... n
p = the probability of success in a single trial
q = the probability of failure in a single trial
(i.e. q = 1 − p)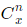 is a combination
is a combination
P(X) gives the probability of successes in n binomial trials.
Mean and Variance of Binomial Distribution
If p is the probability of success and q is the probability of failure in a binomial trial, then the expected number of successes in n trials (i.e. the mean value of the binomial distribution) is
E(X) = μ = np
The variance of the binomial distribution is
V(X) = σ2 = npq
Note: In a binomial distribution, only 2 parameters, namely n and p, are needed to determine the probability.
Example 1.
A die is tossed 3 times. What is the probability of
(a) No fives turning up?
(b) 1 five?
(c) 3 fives?
Solution.
This is a binomial distribution because there are only 2 possible outcomes (we get a 5 or we don't).
Now, n=3 for each part. Let X = number of fives appearing.
(a) Here, x = 0.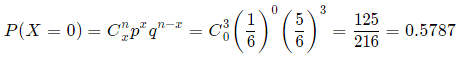
(b) Here, x = 1.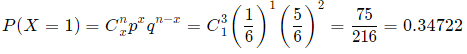
(c) Here, x = 3.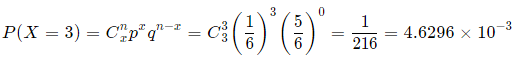
Example 2.
Hospital records show that of patients suffering from a certain disease, 75% die of it. What is the probability that of 6 randomly selected patients, 4 will recover?
Solution.
This is a binomial distribution because there are only 2 outcomes (the patient dies, or does not).
Let X = number who recover.
Here, n = 6 and x = 4.
Let p = 0.25 (success, that is, they live), q = 0.75 (failure, i.e. they die).
The probability that 4 will recover: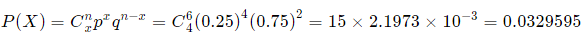
Histogram of this distribution:
We could calculate all the probabilities involved and we would get: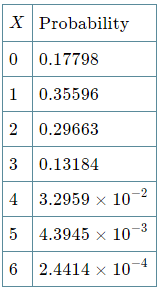
The histogram is as follows: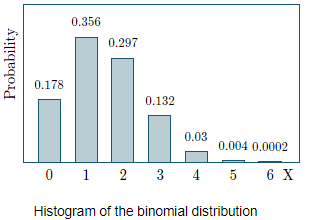
It means that out of the 6 patients chosen, the probability that:
- None of them will recover is 0.17798,
- One will recover is 0.35596, and
- All 6 will recover is extremely small.
Example 3.
In the old days, there was a probability of 0.8 of success in any attempt to make a telephone call. (This often depended on the importance of the person making the call, or the operator's curiosity!)
Calculate the probability of having 7 successes in 10 attempts
Solution.
Probability of success p = 0.8, so q = 0.2.
X = success in getting through.
Probability of 7 successes in 10 attempts:
Probability = P(X = 7)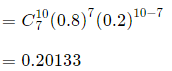
Histogram
We use the following function
C(10,x)(0.8)x (0.2)10−x
to obtain the probability histogram: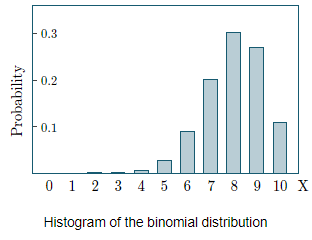
Example 4.
A (blindfolded) marksman finds that on the average he hits the target 4 times out of 5. If he fires 4 shots, what is the probability of
(a) more than 2 hits?
(b) at least 3 misses?
Solution.
Here, n = 4, p = 0.8, q = 0.2.
Let X = number of hits.
Let x0 = no hits, x1 = 1 hit, x2 = 2 hits, etc.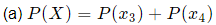
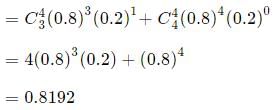
(b) 3 misses means 1 hit, and 4 misses means 0 hits.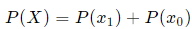
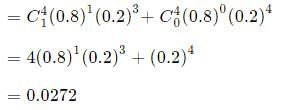
Example 5.
The ratio of boys to girls at birth in Singapore is quite high at 1.09:1.
What proportion of Singapore families with exactly 6 children will have at least 3 boys? (Ignore the probability of multiple births.)
[Interesting and disturbing trivia: In most countries the ratio of boys to girls is about 1.04:1, but in China it is 1.15:1.]
Solution.
The probability of getting a boy is 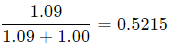
Let X = number of boys in the family.
Here,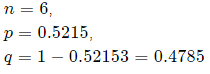
When x = 3: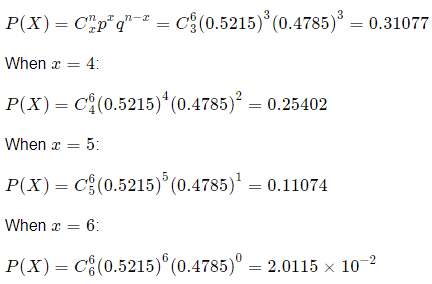
So the probability of getting at least 3 boys is:
Probability = P(X ≥ 3)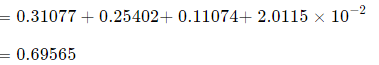
NOTE: We could have calculated it like this: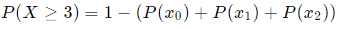
Example 6.
A manufacturer of metal pistons finds that on the average, 12% of his pistons are rejected because they are either oversize or undersize. What is the probability that a batch of 10 pistons will contain
(a) no more than 2 rejects?
(b) at least 2 rejects?
Solution.
Let X = number of rejected pistons
(In this case, "success" means rejection!)
Here,n = 10, p = 0.12, q = 0.88.
(a) No rejects. That is, when x = 0: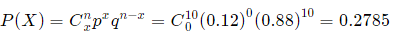
One reject. That is, when x = 1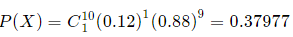
Two rejects. That is, when x = 2: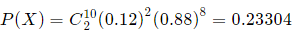
So the probability of getting no more than 2 rejects is: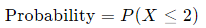
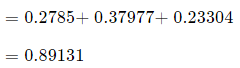
(b) We could work out all the cases for X = 2,3,4,…,10, but it is much easier to proceed as follows:
Probablity of at least 2 rejects
Histogram
Using the function g(x) = C(10,x)(0.12)x (0.88)10−x and finding the values at 0,1,2,…, gives us the histogram: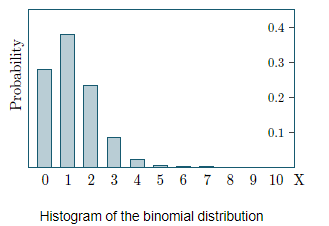
|
124 videos|176 docs
|
FAQs on Binomial Distribution - Business Mathematics and Statistics - B Com
| 1. What is the binomial distribution? |  |
| 2. How is the binomial distribution calculated? |  |
| 3. What are the characteristics of a binomial distribution? |  |
| 4. In what situations can the binomial distribution be applied? |  |
| 5. How does the binomial distribution differ from other probability distributions? |  |
















