Binomial Expansion for Positive Integral Index | Mathematics (Maths) Class 11 - Commerce PDF Download
Binomial Expansion
Binomial theorem is a sorted way (or formula) of expanding expressions that are raised to some large power. Let us first understand what are binomial expressions with the help of some examples.
Example 1 (a+b)2
Suppose we have an expression (a+b)2. Here (a+b)2 is an expression with an operator +, now we have to expand it. Well, we all know its formula
(a+b)2=a2+b2+2ab
This type of expansion of an expression is called binomial expansion.
Example 2 (a+b)3
The second expression is (a+b)3. To expand this, we have the formula
(a+b)3=a3+b3+3ab(a+b)
Example 3 (a+b)6
To expand this expression we have two ways. First, write (a+b) 6 times and multiply each one by one, like below:
(a+b)×(a+b)×(a+b)×(a+b)×(a+b)×(a+b)
Another way is to divide 6 as 2*3. In that case first apply (a+b)2 formula first, then multiply that expression 3 times, i.e
(a+b)2=a2+b2+2ab
And then multiply them three times. The above two methods are very lengthy, time consuming and chances of mistakes are also high. So to avoid such errors and mistakes we use binomial theorem.
Explanation of Binomial Theorem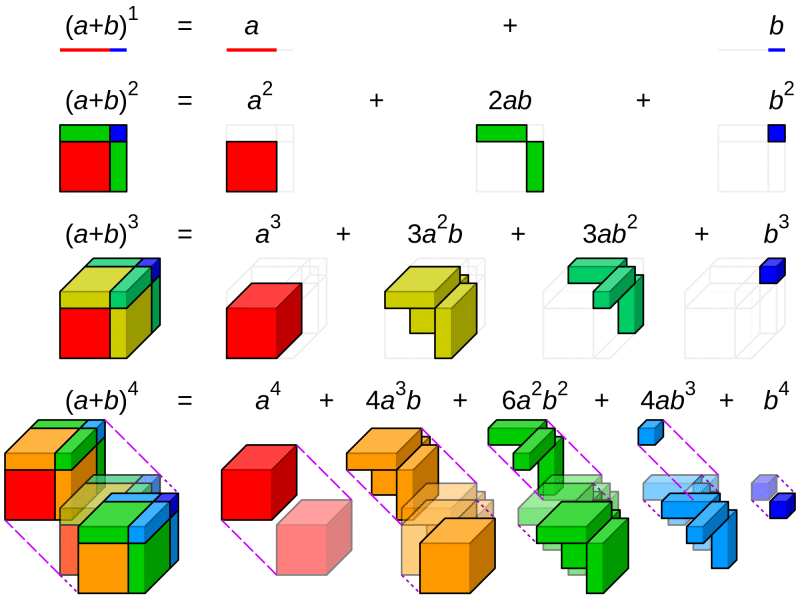
As stated earlier, the binomial theorem is used for the larger power of any expression. Let’s start with the formula-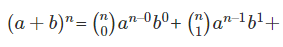
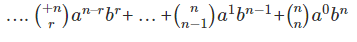
Above expression is an expansion of the binomial theorem. Some important points to remember of this theorem:
• n must be positive integer
• Binomial expansion always starts from 0 to the highest power of n. For example, if the value of n is 4 then expansion will start from 0 to 4.
• C is called the combination. Here is its formula- (nr) = n!n!(n−r)!
Here n is always greater than r. For example- if n is 12 and r is 2,
n!=12!=12×11×10×9×8×7×6×5×4×3×2×1
r!=2!=2×1
(n−r)!=10!=10×9×8×7×6×5×4×3×2×1
12!÷(10!×2!)=12×11×10!÷(10!×2)
On solving , the final answer is 66. This is the way to solve combinations and without combinations, it will be very difficult to solve binomial expansions.
• Power of a is the subtraction of n and r. Power of b is always r. That’s why in the first expansion power of a is n-0 and b is 0. It can be seen in the expansion that the power of ‘b’ is increasing because the value of r is also increasing.
Conclusion
Binomial Theorem is always easier than multiplying the big and long expressions. To avoid error and mistakes, first practice the combinations formula with some examples, then try practising the binomial theorem. Binomial expansion is a simple combination of multiplication, division, addition and subtraction.
Solved Examples
Question: Sample Example of the Binomial Theorem.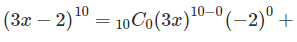
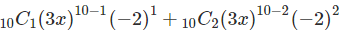
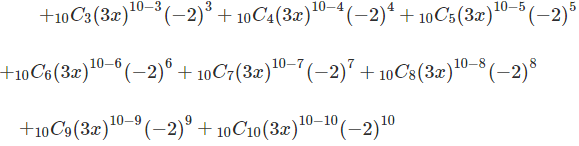
Solution: In this example we are expanding (3x – 2)10. According to the formula, here a is 3x and b is -2 and n is 10. So we are expanding it from 0 to 10. The value of n varies from 0 to 10. On solving the above combinations and values, here is the consolidated data:
(3x−2)10=(1)(59049)x10(1)+(10)(19683)x9(–2)+(45)(6561)x8(4)
+(120)(2187)x7(–8)+(210)(729)x6(16)+(252)(243)x5(–32)
+(210)(81)x4(64)+(120)(27)x3(–128)+(45)(9)x2(256)
+(10)(3)x(–512)+(1)(1)(1)(1024)
And here is the final result,
(3x−2)10=59049x10–393660x9+1180980x8–2099520x7
+2449440x6–1959552x5+1088640x4–414720x3
+103680x2–15360x+1024
|
75 videos|238 docs|91 tests
|
FAQs on Binomial Expansion for Positive Integral Index - Mathematics (Maths) Class 11 - Commerce
| 1. What is the binomial expansion for positive integral index? |  |
| 2. How do you find the coefficients in the binomial expansion for positive integral index? |  |
| 3. What is the significance of the binomial expansion for positive integral index? |  |
| 4. Can the binomial expansion be used for negative or fractional indices? |  |
| 5. Are there any limitations or restrictions in using the binomial expansion for positive integral index? |  |


















