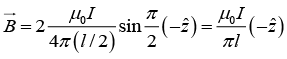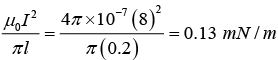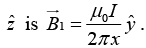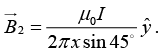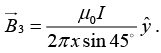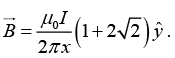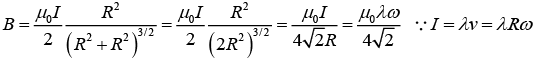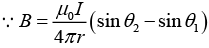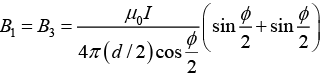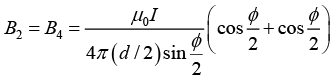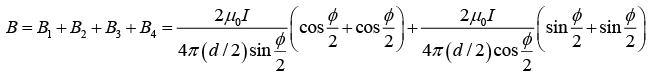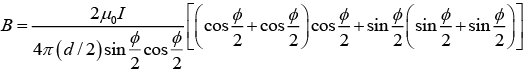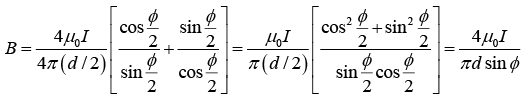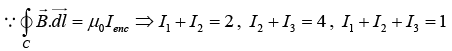Biot Savart Law, Ampere's Law & Magnetic Force: Assignment | Electricity & Magnetism - Physics PDF Download
Q.1. A square loop is placed near an infinite straight wire as shown in figure. The loop and wire carry a steady current I2 and I1 respectively. Then find the net force acting on the square loop.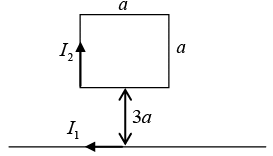
The force on the two sides cancels.
At the bottom,
At the top,
Thus Net Force
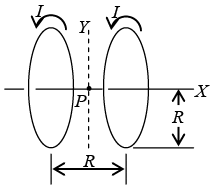
Q.2. A system of two circular co-axial coils carrying equal currents I along same direction having equal radius R and separated by a distance R (as shown in the figure below). Find the magnitude of magnetic field at the midpoint P.
Q.3. Two long conductors are arranged as shown below to form overlapping cylinders, each of radius R, whose centers are separated by a distance d. Current of density J flows into the plane of the page along the shaded part of one conductor and an equal current flows out of the plane of the page along the shaded portion of the other, as shown. What are the magnitude and direction of the magnetic field at point A ?
(Assumes that the vacuum region in the center is small compared to the area of the conductors)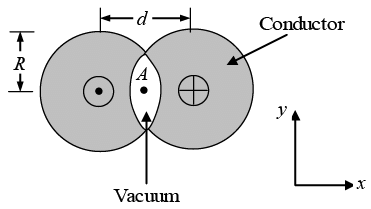
Recall Ampere’s Law,
Thus, the field from each conductor is B(2πr) = μ0JπR2, where, Ienc = JπR2 and R is the radius of the conductor.
(This is a good approximation of the current, as one assumes that the vacuum region in the center is small compared to the area of the conductors.)
Making the approximation that R ≈ d / 2, one has
Since both fields contribute in the center, the field is twice that,
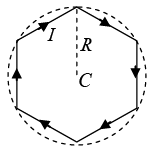
Q.4. A conducting wire is in the shape of a regular hexagon, which is inscribed inside an imaginary circle of radius R, as shown in figure. A current I flows through the wire. Find the magnitude of the magnetic field at the center of the circle.
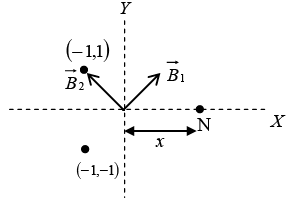
Q.5. Consider two infinitely long wires parallel to the z -axis carrying the same current I. One wire passes through the point L with coordinates (-1,1) and the other through M with coordinates (-1,1) in the XY planes shown in the figure. The direction of the current in both the wires is in the positive z -direction.
(a) Find the value of 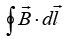 along the semicircular closed path of radius 2 units shown in the figure.
along the semicircular closed path of radius 2 units shown in the figure.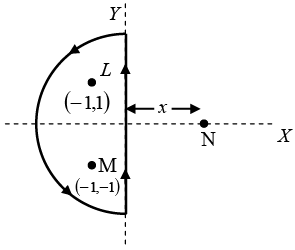
(b) A third long wire carrying current I and also perpendicular to the XY plane is placed at a point N with coordinates (x,0) so that the magnetic field at the origin is doubled. Find x and the direction of the current in the third wire.
(a)
(b)
Resultant ofis
The current in the third wire is inward so that
Q.6. Find the magnitude and direction of a force vector acting on a unit length of a thin wire, carrying a current I = 8.0A, at a point O, if the wire is bent as shown in
(a) Figure (a), with curvature radius R = 10 cm;
(b) Figure (b), the distance between the long parallel segments of the wire being equal to l = 20 cm.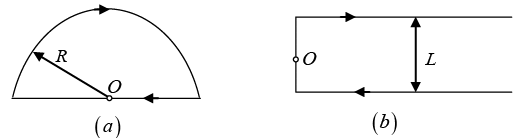
(a) The magnetic field at O is only due to the curved path, as for the line element,
Force per unit length
Magnitude of force per unit length is
(b) In this part, the magnetic field at O will be effective only due to semi infinite segments of wire.Hence
Force per unit length
Magnitude of force per unit length is
Q.7. Three long, straight wires in the xz -plane, each carrying current I , cross at the origin of coordinates, as shown in the figure above. Let 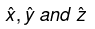 denote the unit vectors in the x-, y- and z- directions, respectively. Find the magnetic field B as a function of x, with y = 0 and z = 0 .
denote the unit vectors in the x-, y- and z- directions, respectively. Find the magnetic field B as a function of x, with y = 0 and z = 0 .
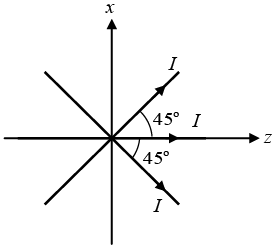
Take a point ( x, 0, 0 ) on the x -axis.
At this point the magnetic field due to the wire along
Due to the wire crossing the first and third quadrants is
Due to the wire crossing the second and fourth quadrants is
Thus, the net magnetic field at point ( x, 0, 0 ) is
Q.8. A ring of radius R carries a linear charge density λ and it is rotating with angular speed ω. Then
(a) Find the magnetic field at a distance R above its center.
(b) Find the magnetic field at its center.
(a)
(b)
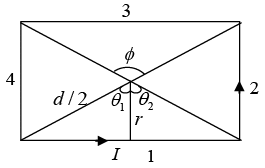
Q.9. Consider a rectangular wire frame whose diagonal length is d and the angle between the diagonal is ϕ as shown in figure. If the current flowing in the frame is I, then the magnetic field B at the centre of the frame is 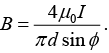
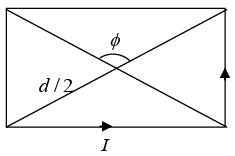
where θ1 = -ϕ/2 and θ2 = ϕ/2
Magnetic field due to segment 1 and 3 is
Magnetic field due to segment 2 and 4 isHence, the magnitude of total magnetic field is
Q.10. Three infinitely-long conductors carrying currents I1 ,I2 and I3 lie perpendicular to the plane of the paper as shown in the figure. If the value of the integral 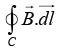 for the loops C1 ,C2 and C3 are 2μ0 , 4μ0 and μ0 in the units of N/A respectively, then find I1 , I2 and I3.
for the loops C1 ,C2 and C3 are 2μ0 , 4μ0 and μ0 in the units of N/A respectively, then find I1 , I2 and I3.
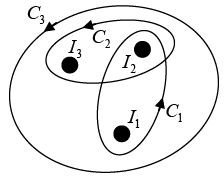
⇒ I1 = -3A, I2 = 5A and I3 =-1A.
I1 = 3A into the paper, I2 = 5A out of the paper and I3 = 1A into the paper
|
82 videos|32 docs|22 tests
|
FAQs on Biot Savart Law, Ampere's Law & Magnetic Force: Assignment - Electricity & Magnetism - Physics
| 1. What is the Biot Savart Law? |  |
| 2. What is Amperes Law? |  |
| 3. How are Biot Savart Law and Amperes Law related? |  |
| 4. What is the Magnetic Force on a charged particle moving in a magnetic field? |  |
| 5. How are Biot Savart Law and Amperes Law applied in practical scenarios? |  |

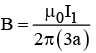
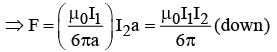
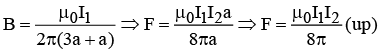
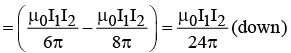
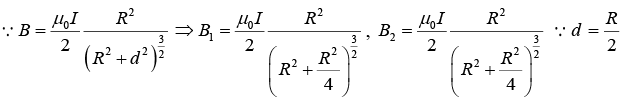
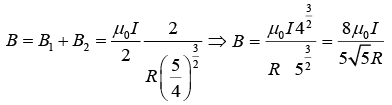
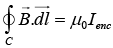
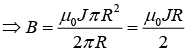
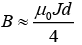
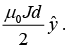
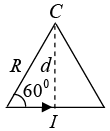
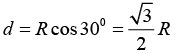
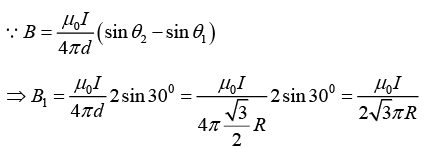
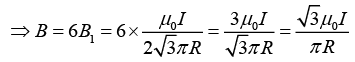
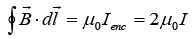
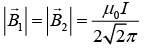
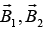 is
is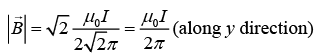
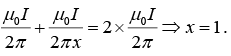
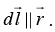
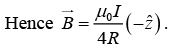

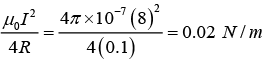
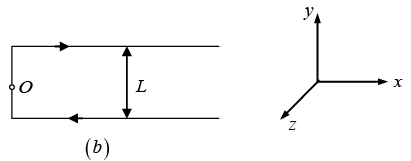 Hence
Hence