Boundary Value Problems | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
Introduction
A boundary value problem for a given differential equation consists of finding a solution of the given differential equation subject to a given set of boundary conditions. A boundary condition is a prescription some combinations of values of the unknown solution and its derivatives at more than one point.Let I = (a, b) ⊆ R be an interval. Let p, q, r : (a, b) → R be continuous functions.
Throughout this chapter we consider the linear second order equation given by
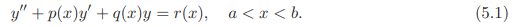 Corresponding to ODE (5.1), there are four important kinds of (linear) boundary conditions. They are given by
Corresponding to ODE (5.1), there are four important kinds of (linear) boundary conditions. They are given by
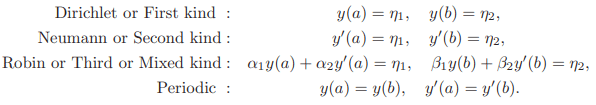 Remark 5.1 (On periodic boundary condition) If the coefficients of ODE (5.1) are periodic functions with period l = b − a and if φ is a solution of ODE (5.1) (note that this solution exists on R), then ψ defined by ψ(x) = φ(x + l) is also a solution. If φ satisfies the periodic boundary conditions, then ψ(a) = φ(a) and ψ ′ (a) = φ ′ (a). Since solutions to IVP are unique in the present case, it must be that ψ ≡ φ. In other words, φ is a periodic function of period l.
Remark 5.1 (On periodic boundary condition) If the coefficients of ODE (5.1) are periodic functions with period l = b − a and if φ is a solution of ODE (5.1) (note that this solution exists on R), then ψ defined by ψ(x) = φ(x + l) is also a solution. If φ satisfies the periodic boundary conditions, then ψ(a) = φ(a) and ψ ′ (a) = φ ′ (a). Since solutions to IVP are unique in the present case, it must be that ψ ≡ φ. In other words, φ is a periodic function of period l.
Boundary Value Problems do not behave as nicely as Initial value problems. For, there are BVPs for which solutions do not exist; and even if a solution exists there might be many more. Thus existence and uniqueness generally fail for BVPs. The following example illustrate all the three possibilities.
Adjoint forms, Lagrange identity
In mathematical physics there are many important boundary value problems corresponding to second order equations. In the studies of vibrations of a membrane, vibrations of a structure one has to solve a homogeneous boundary value problem for real frequencies (eigen values). As is wellknown in the case of symmetric matrices that there are only real eigen values and corresponding eigen vectors form a basis for the underlying vector space and thereby all symmetric matrices are diagonalisable. Self-adjoint problems can be thought of as corresponding ODE versions of symmetric matrices, and they play an important role in mathematical physics.Let us consider the equation
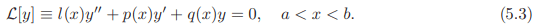
Integrating z [y] by parts from a to x, we have
[y] by parts from a to x, we have
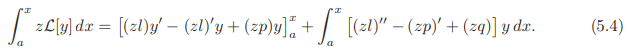
If we define the second order operator 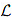 ∗ by
∗ by
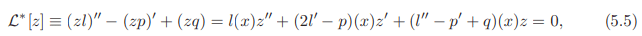
then the equation (5.4) becomes
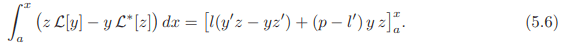
The operator 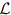 ∗ is called the adjoint operator corresponding to the operator
∗ is called the adjoint operator corresponding to the operator 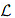 . It can be easily verified that adjoint of
. It can be easily verified that adjoint of 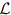 ∗ is L itself. If
∗ is L itself. If 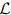 and
and 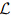 ∗ are the same, then L is said to be self-adjoint .Thus, the necessary and sufficient condition for
∗ are the same, then L is said to be self-adjoint .Thus, the necessary and sufficient condition for 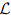 to be self-adjoint is that
to be self-adjoint is that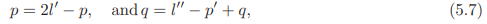 which is satisfied if
which is satisfied if
 Thus if L is self-adjoint, we have
Thus if L is self-adjoint, we have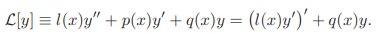 A general operator
A general operator 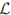 may not be self-adjoint but it can always be converted into a self-adjoint by suitably multiplying
may not be self-adjoint but it can always be converted into a self-adjoint by suitably multiplying 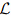 with a function.
with a function.
Two-point boundary value problem
In this section we are going to set up the notations that we are going to use through out our discussion of BVPs. We consider the linear nonhomogeneous second order in the self-adjoint form described below:
Note: that the boundary conditions are in the most general form, and they include the first three conditions given at the beginning of our discussion on BVPs as special cases.
Let us introduce some nomenclature here
Assume hypothesis (HBVP). A nonhomogeneous boundary value problem consists of solving
 for given constants η1 and η2, and a given continuous function f on the interval [a, b].
for given constants η1 and η2, and a given continuous function f on the interval [a, b].
The associated homogeneous boundary value problem is then given by
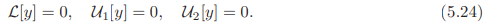 Let us list some properties of the solutions for BVP that are consequences of the linearity of the differential operator
Let us list some properties of the solutions for BVP that are consequences of the linearity of the differential operator 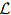 .
.
Fundamental solutions, Green’s functions
Fundamental solution of an ODE gives rise to a representation (integral) formula for solution of the nonhomogeneous equation. When we want to take care of boundary conditions, we impose boundary conditions on fundamental solutions and get Green’s functions. Thus Green’s functions give rise to a representation formula for solution of the nonhomogeneous BVP. The concepts of a fundamental solution as well as a Green’s function are defined in terms of the homogeneous BVPvassociated to the nonhomogeneous BVP.Let Q denote the square Q := [a, b] × [a, b] in the xξ-plane. Let us partition Q by the line x = ξ and call the two resulting triangles Q1 and Q2. Let
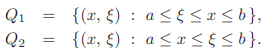 Note that the diagonal x = ξ belongs to both the triangles.
Note that the diagonal x = ξ belongs to both the triangles. 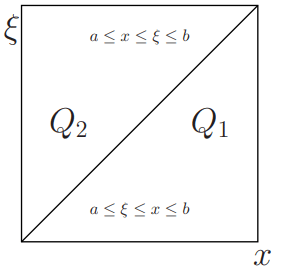
Fundamental solution: A function γ(x, ξ) defined in Q is called a fundamental solution of the homogeneous differential equation  [y] = 0 if it has the following properties:
[y] = 0 if it has the following properties:
(i) The function γ(x, ξ) is continuous in Q.
(ii) The first and second order partial derivatives w.r.t. variable x of the function γ(x, ξ) exist and continuous up to the boundary on Q1 and Q2.
(iii) Let ξ ∈ [a, b] be fixed. Then γ(x, ξ), considered as a function of x, satisfies  [γ(., ξ)] = 0 at every point of the interval [a, b], except at ξ.(iv) The first derivate has a jump across the diagonal x = ξ, of magnitude 1/p, i.e.,
[γ(., ξ)] = 0 at every point of the interval [a, b], except at ξ.(iv) The first derivate has a jump across the diagonal x = ξ, of magnitude 1/p, i.e.,
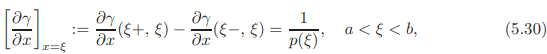
Construction of Green’s functions
In this paragraph we are going to construct Green’s functions under the assumption that the homogeneous BVP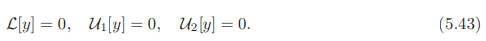 has only trivial solution. Let (λ1, λ2) 6= (0, 0) be such that a1λ1 + a2λ2 = 0 and let φ1 be solution of
has only trivial solution. Let (λ1, λ2) 6= (0, 0) be such that a1λ1 + a2λ2 = 0 and let φ1 be solution of 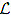 [y] = 0 satisfying φ1(a) = λ1 and φ ′ 1 (a) = λ2. Choose another solution φ2 of
[y] = 0 satisfying φ1(a) = λ1 and φ ′ 1 (a) = λ2. Choose another solution φ2 of 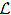 [y] = 0 similarly. This way of choosing φ1 and φ2 make sure that both are non-trivial solutions.
[y] = 0 similarly. This way of choosing φ1 and φ2 make sure that both are non-trivial solutions.Note that φ1 and φ2 form a fundamental pair of solutions of
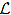 [y] = 0, since we assumed that homogeneous BVP has only trivial solutions.By Lagrange’s identity (5.20), we get d dx p(φ ′ 1φ2 − φ1φ ′ 2 ) = 0.
[y] = 0, since we assumed that homogeneous BVP has only trivial solutions.By Lagrange’s identity (5.20), we get d dx p(φ ′ 1φ2 − φ1φ ′ 2 ) = 0.This implies p(φ ′ 1φ2 − φ1φ ′ 2 ) ≡ c, a constant and non-zero, (5.44)
as a consequence of (φ ′ 1φ2 − φ1φ ′ 2 ) being the wronskian corresponding to a fundamental pair of solutions.
Green’s function is then given by
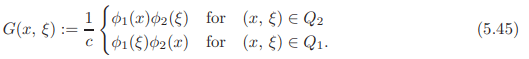 Verifying that G(x, ξ) has the required properties for it to be a Green’s function is left as an exercise.
Verifying that G(x, ξ) has the required properties for it to be a Green’s function is left as an exercise.Generalised Green’s function
In Section 5.3 we constructed Green’s function for the homogeneous BVP when the latter problem had only trivial solutions. Now we investigate the case where the homogeneous BVP has non-trivial solutions.Let us look at what happens in the case of linear system of equations of size k in k variables. Let A be a k × k matrix, and b ∈ R k . Suppose that Ax = 0 has non-trivial solutions. In this case we know that Ax = b does not have solution for every b ∈ R k . We also know that Ax = b has a solution if and only if b belongs to orthogonal complement of a certain subspace of R k , i.e., b must satisfy a compatibility condition. Note that, in this case, if Ax = b has one solution, then there are infinitely many solutions.
We are going to see that there exists an analogue of Green’s function, called Generalised Green’s function. We also prove that a situation similar to that of matricial analogy given above occurs here too; and the compatibility condition for the existence of a solution to nonhomogeneous BVP is a kind of Fredholm alternative.
Let us recall the notations Q1 and Q2.
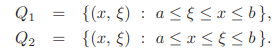
Generalised Green’s function: Let φ0 be a solution of 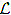 [y] = 0 with homogeneous boundary conditions, such that
[y] = 0 with homogeneous boundary conditions, such that 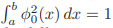 . A function Γ(x, ξ) defined in Q is called a generalised Green’s function if Γ has the following properties:
. A function Γ(x, ξ) defined in Q is called a generalised Green’s function if Γ has the following properties:
(i) The function Γ(x, ξ) is continuous in Q.
(ii) The first and second order partial derivatives w.r.t. variable x of the function Γ(x, ξ) exist and continuous up to the boundary on Q1 and Q2.
(iii) Let ξ ∈ [a, b] be fixed. Then γ(x, ξ), considered as a function of x, satisfies
 at every point of the interval [a, b], except at ξ, satisfying the homogeneous boundary conditions U1[y] = 0 and U2[y] = 0.
at every point of the interval [a, b], except at ξ, satisfying the homogeneous boundary conditions U1[y] = 0 and U2[y] = 0.
(iv) The first derivate has a jump across the diagonal x = ξ, of magnitude 1/p, i.e.,
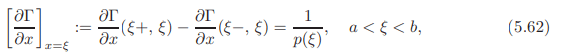
(v) The function Γ(x, ξ) satisfies the condition

The following result characterises the class of functions f, for which the nonhomogeneous equation 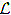 [y] = f has a solution satisfying homogeneous boundary conditions.
[y] = f has a solution satisfying homogeneous boundary conditions.
Solved Numericals
Q1. We have 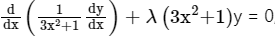 ,y = 0, y(0) = 0, y(π) = 0 then the corresponding eigen value and eigen function are:
,y = 0, y(0) = 0, y(π) = 0 then the corresponding eigen value and eigen function are:
Solution:
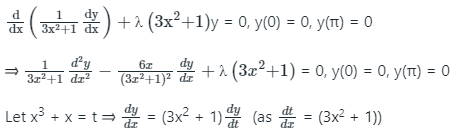
Differentiating both sides we get
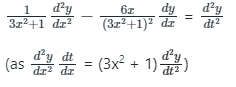
Then the ODE becomes
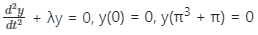
Auxillary equation is

Solution is
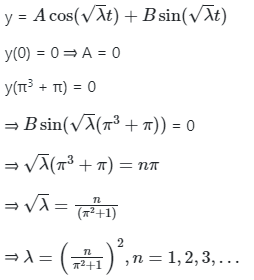
Hence solution is
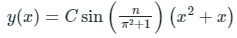
Q2. Consider the differential equation 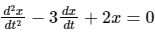 .If x = 0 at t = 0 and x = 1 at t = 1, the value of x at t = 2 is:
.If x = 0 at t = 0 and x = 1 at t = 1, the value of x at t = 2 is:
Solution:
- Let d/dx = D
- So, the differential equation becomes : (D2 - 3D + 2)x = 0
- Now, as x cannot be zero, the function in the bracket will be zero.
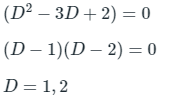
Substituting the value in the solution: 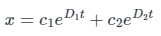
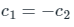
Applying the second boundary condition:

Q3. For λ ∈ ℝ, consider the boundary value problem
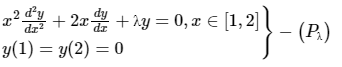
Which of the following statement is true?
Solution: Given: Given D.E. is
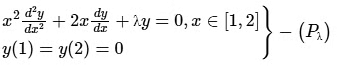
Concept used: We will put
Putting
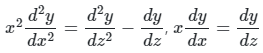
Now or D.E. reduced to
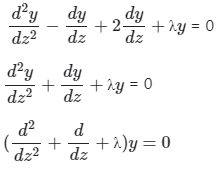
Now, using the notation  our equation reduced to
our equation reduced to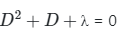
Auxillary equation
m2 + m + λ = 0
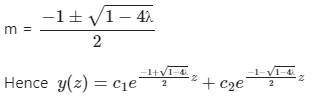
Converting it into the function of x by putting 
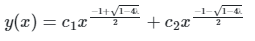
Now using initial values
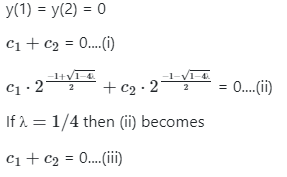
So (i) and (ii) has a trivial solution for
Except that it has non-trivial independent solution.
|
44 videos|109 docs|58 tests
|
FAQs on Boundary Value Problems - Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
| 1. What are adjoint forms and how are they related to boundary value problems in mechanical engineering? |  |
| 2. How does the Lagrange identity help in solving boundary value problems in mechanical engineering? |  |
| 3. What is the significance of fundamental solutions and Green's functions in the context of boundary value problems in mechanical engineering? |  |
| 4. How are Green's functions constructed and utilized in the solution of boundary value problems in mechanical engineering? |  |
| 5. What is a generalised Green's function and how is it different from a regular Green's function in the context of boundary value problems in mechanical engineering? |  |
















