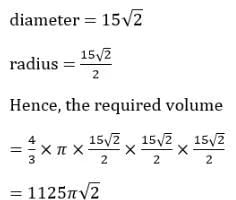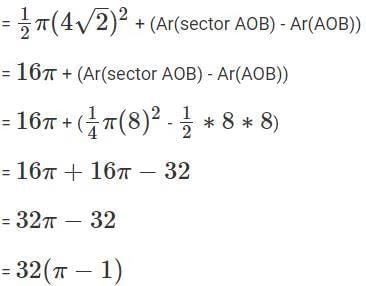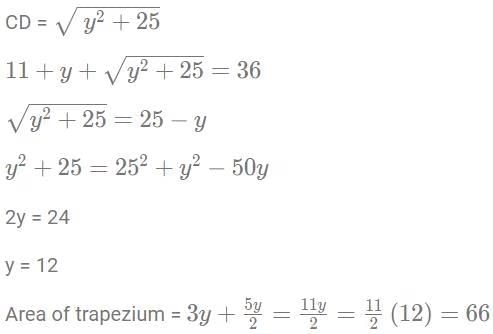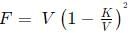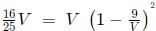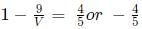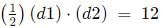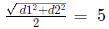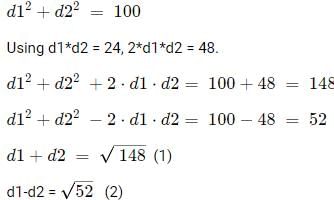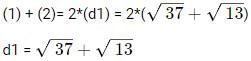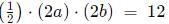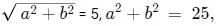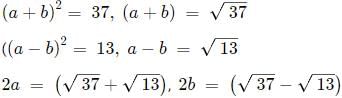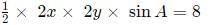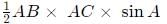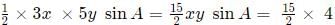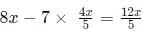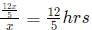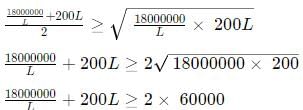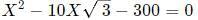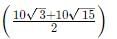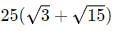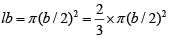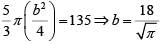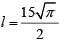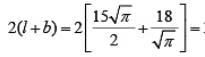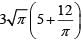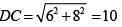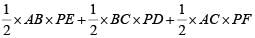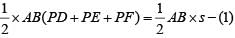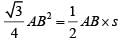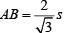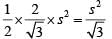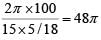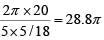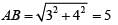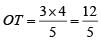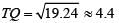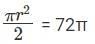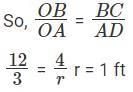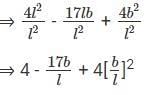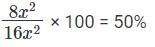Mensuration CAT Previous Year Questions with Answer PDF
2024
Q1: The surface area of a closed rectangular box, which is inscribed in a sphere, is 846 sq. cm., and the sum of the lengths of all its edges is 144 cm. The volume, in cubic cm, of the sphere is
(a) 1125π|
(b) 1125π√2
(c) 750π√2
(d) 750π
Ans: b
Sol:
Q2: The coordinates of the three vertices of a triangle are: (1, 2), (7, 2), and (1, 10). Then the radius of the incircle of the triangle is
Ans: 2
Sol: Given,
The three vertices are: (1,2), (7,2) and (1,10)
The three side lengths are 6, 8 and 10 respectively.
These are the sides of a right angled triangle.
So, Area = 1/2 × 6 × 8 = 24 sq. units
Inradius = area / semi-perimeter = 24 / 12 = 2 units
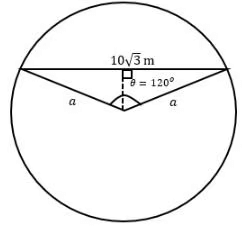
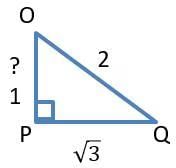
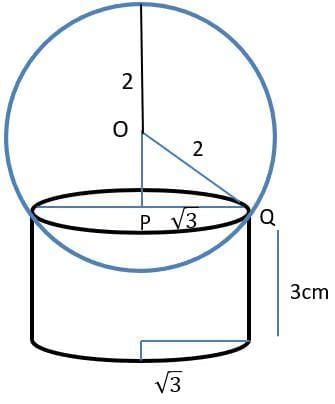
Q3: A circular plot of land is divided into two regions by a chord of length 10√3 meters such that the chord subtends an angle of 120° at the center. Then, the area, in square meters, of the smaller region is
(a) 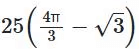
(b) 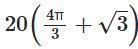
(c) 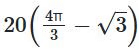
(d) 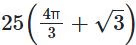
Ans: a
Sol:
Now, we have
θ = 120° where θ is the angle subtended by a chord at the center.
Length of chord = 10√3 = 2r sin (θ / 2)
2 * r * sin60 = 10√3
r = 10
So, the area of the smaller region = area of the sector – area of the triangle = (θ / 360) * πr2 – (1 / 2) * |absinθ|
= (120 / 360) * π * 102 – (1 / 2) * |102 * sin120°| = (100π / 3) – |50 * cos30°| = (100π / 3) – 25√3 = 25((4π / 3) – √3)
Hence, option A is the correct answer.
Q4: A regular octagon ABCDEFGH has sides of length 6 cm each. Then, the area, in sq. cm, of the square ACEG is
(a) 72(2 + √2)
(b) 36(1 + √2)
(c) 36(2 + √2)
(d) 72(1 + √2)
Ans: c
Sol: As we know that
diagonal of octagon ABCDEFGH = side * √(2 + √2)Area of square ACEG = diagonal2
Hence, option C is the correct answer.
2023
Q1: In a right-angled triangle ABC, the altitude AB is 5 cm, and the base BC is 12 cm. P and Q are two points on BC such that the areas of ΔABP, ΔABQ and ΔABC are in arithmetic progression. If the area of ΔABC is 1.5 times the area of ΔABP, the length of PQ, in cm, is
Ans: 2
Sol: The construction of the triangle according to the question is as follows:
2022
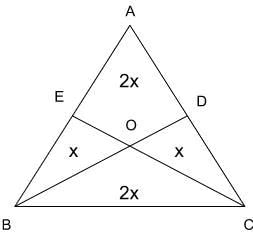
Q1: Suppose the medians BD and CE of a triangle ABC intersect at a point O. If area of triangle ABC is 108 sq. cm., then, the area of the triangle EOD, in sq. cm., is [2022]
Ans: 9
Sol:
O is the centroid of the triangle ABC, that means,
BO : OD = 2 : 1
CO : OE = 2 : 1
Ar(BOC) : Ar(ODC) = 2 : 1
Ar(COB) : Ar(OEB) = 2 : 1
Since BD is the median, Ar(BDA) = Ar(BDC)
This means Ar(AEOD) = 2x
2x + x + x + 2x = 108
6x = 108
Ar(AEOD) = 2x = 36
Since ED is the line joining the midpoints of AB and AC, Ar(AED) = ¼ Ar(ABC)
Ar(AED) = ¼ Ar(108) = 27Ar(EOD) = Ar(AEOD) - Ar(AED) = 36 - 27 = 9 sq cm
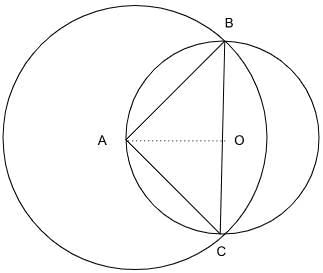
Q2: In a triangle ABC, AB = AC = 8cm. A circle drawn with BC as diameter passes through A . Another circle drawn with center at A passes through B and C. Then the area, in sq. cm , of the overlapping region between the two circles is [2022]
(a) 16(π−1)
(b) 32(π−1)
(c) 32π
(d) 16π
Ans: b
Sol:
AB = AC = 8cm
Since BC is the diameter, angle A has to right-angled and angle B = angle C = 45 degrees.
Therefore, the radius of the circle centred at O is 4√ 2.
The radius of the circle centred at Aa is 8cm.
The common area between them = (half of the smaller circle) + (and the minor segment created by the chord BC in the bigger circle)
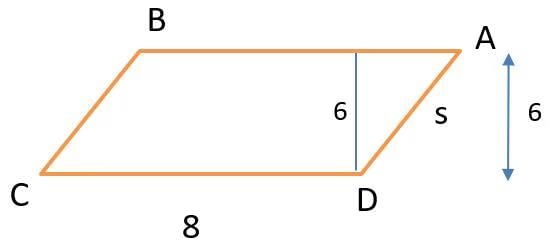
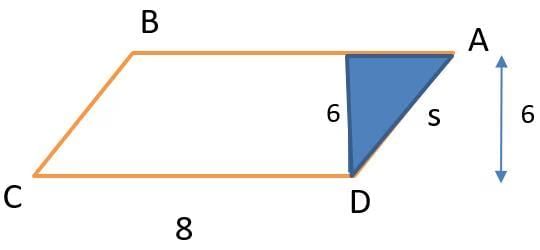
Q3: A trapezium ABCD has side AD parallel to BC, ∠BAD = 90°, BC = 3 cm and AD = 8 cm. If the perimeter of this trapezium is 36 cm, then its area, in sq. cm, is
Ans: 66
Sol:
2021
Q1: If the area of a regular hexagon is equal to the area of an equilateral triangle of side 12 cm, then the length, in cm, of each side of the hexagon is
(a) 4√6
(b) 6√6
(c) √6
(d) 2√6
Ans: d
Sol: Area of a regular hexagon =Area of an equilateral triangle =
where a = side of the triangleSince the area of the two figures are equal, we can equate them as folllows:
On simplifying: x2 = 24
Q2: From a container filled with milk, 9 litres of milk are drawn and replaced with water. Next, from the same container, 9 litres are drawn and again replaced with water. If the volumes of milk and water in the container are now in the ratio of 16 : 9, then the capacity of the container, in litres, is [2021]
Ans: 45
Sol: Let initial volume be V, final be F for milk.
The formula is given by :n is the number of times the milk is drawn and replaced.
so we get
here K =9
we get
we get
If considering 1 - 9/V = -4/5
V = 5, but this is not possible because 9 liters is drawn every time.
Hence : 1− 9/V = 4/5
V = 45 litres
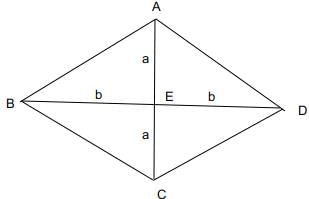
Q3: If a rhombus has area 12 sq cm and side length 5 cm, then the length, in cm, of its longer diagonal is [2021]
(a) 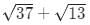
(b) 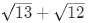
(c) 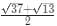
(d) 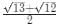
Ans: a
Sol: All the sides of the rhombus are equal.
The area of a rhombus is 12 cm2.
Considering d1 to be the length of the longer diagonal, d2 to be the length of the shorter diagonal.
The area of a rhombus is
d1 x d2 = 24.
The length of the side of a rhombus is given byThis is because the two diagonals and a side from a right-angled triangle with sides d1/2, d2/2 and the side length.
Hence,
or
In a rhombus the area of a Rhombus is given by :
The diagonals perpendicularly bisect each other. Considering the length of the diagonal to be 2a, 2b.
The area of a Rhombus is :
ab = 6.
The length of each side is :
2a is longer diagonal which is equal to
Q4: The sides AB and CD of a trapezium ABCD are parallel, with AB being the smaller side. P is the midpoint of CD and ABPD is a parallelogram. If the difference between the areas of the parallelogram ABPD and the triangle BPC is 10 sq cm, then the area, in sq cm, of the trapezium ABCD is [2021]
(a) 30
(b) 40
(c) 25
(d) 20
Ans: a
Sol: We are given that :Let DP =x
So AB =x
Now DP=CP
So CD = 2x
Now let height of trapezium be h
we can say A(Parallelogram ABPD ) = xh
And A (BPC) = 1/2xh
Now by condition xh - 1/2xh = 10
xh / 2 = 10
so xh =20
Now therefore area of trapezium ABCD = 1/2 (x + 2x)h = 3/2xh = 30
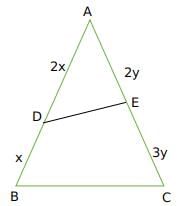
Q5: Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is [2021]
Ans: 30
Sol: We have :
Now area of ADE = 1/2 x AD x AE x sin A
=
we get xy sinA =4Now Area of triangle ABC
=
We get,
we get Area of ABC = 30
Q6: Two pipes A and B are attached to an empty water tank. Pipe A fills the tank while pipe B drains it. If pipe A is opened at 2 pm and pipe B is opened at 3 pm, then the tank becomes full at 10 pm. Instead, if pipe A is opened at 2 pm and pipe B is opened at 4 pm, then the tank becomes full at 6 pm. If pipe B is not opened at all, then the time, in minutes, taken to fill the tank is [2021]
(a) 144
(b) 140
(c) 264
(d) 120
Ans: a
Sol: Let A fill the tank at x liters/hour and B drain it at y liters/hour
Now as per Condition 1 :
We get Volume filled till 10pm = 8x - 7y (1) .
Here A operates for 8 hours and B operates for 7 hours .
As per condition 2
We get Volume filled till 6pm = 4x - 2y (2)
Here A operates for 4 hours and B operates for 2 hours .
Now equating (1) and (2)
we get 8x - 7y =4x - 2y
so we get 4x = 5y
y = 4x/5
So volume of tank =
So time taken by A alone to fill the tank
= 144 minutes
Q7: The cost of fencing a rectangular plot is ₹ 200 per ft. along one side, and ₹ 100 per ft along the three other sides. If the area of the rectangular plot is 60000 sq. ft, then the lowest possible cost of fencing all four sides, in INR, is [2021]
(a) 120000
(b) 90000
(c) 100000
(d) 160000
Ans: a
Hence, minimum cost = Rs 120000.
Sol: Let us draw the rectangle.
Now, definitely, three sides should be fenced at Rs 100/ft, and one side should be fenced at Rs 200/ft.
In this question, we are going to assume that the L is greater than B.
Hence, the one side painted at Rs 200/ft should be B to minimise costs.
Hence, the total cost = 200B + 100B + 100L + 100L = 300B + 200L
Now, L x B = 60000
B = 60000/L
Hence, total cost = 300B + 200L = 18000000/L + 200L
To minimise this cost, we can use AM > = GM,
Q8: A park is shaped like a rhombus and has area 96 sq m. If 40 m of fencing is needed to enclose the park, the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is [2021]
Ans: 3500
Sol: We can say 40m is the perimeter of the park
so side of rhombus = 10
Now 1/2 x d1 x d2 = 96
So we get d1 x d2 = 192 (1)
And as we know diagonals of a rhombus are perpendicular bisectors of each other :
so,
so we get
Solving (1) and (2)
We get d1 = 12 and d2 = 16
Now the cost, in INR, of laying electric wires along its two diagonals, at the rate of ₹125 per m, is= (12 + 16)(125) = 3500
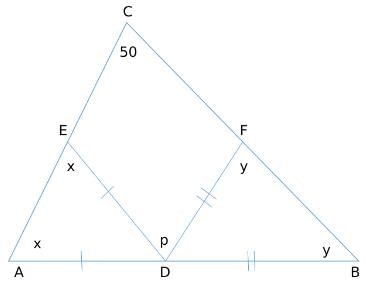
Q9: If a triangle ABC, ∠BCA=50o . D and E are points on AB and AC, respectively, such that AD=DE. If F is a point on BC such that BD=DF , then ∠FDE, in degrees, is equal to [2021]
(a) 72
(b) 80
(c) 100
(d) 96
Ans: b
Sol:We need to find out p.
Angle ADE = 180 - 2x
Angle BDF = 180 - 2y
Now, 180 - 2y + p + 180 - 2x = 180 [Straight line = 180 deg]
p = 2x + 2y - 180
Also, x + y + 50 = 180 [Sum of the angles of triangle = 180]
x + y = 130
p = 260 - 180 = 80 degrees.
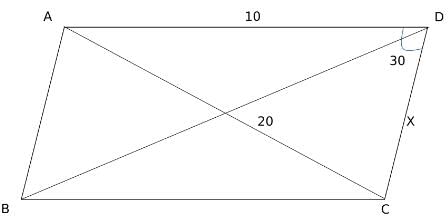
Q10: Let ABCD be a parallelogram. The lengths of the side AD and the diogonal AC are 10cm and 20cm, respectively. If the angle ∠ADC is equal to 30o then the area of the parallelogram, in sq.cm is [2021]
(a) 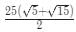
(b) 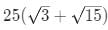
(c) 
(d) 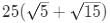
Ans: b
Sol:
Applying cosine rule in triangle ACD,
100 + X2 − 2 × 10 × Xcos30 = 400
Solving we get X =
Hence, area = 10Xsin 30 =
=
2020
Q1: On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches two opposite sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is [2020]
(a) 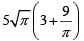
(b) 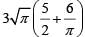
(c) 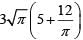
(d) 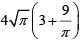
Ans: c
Sol: Let the length and the breadth of the rectangle be l and b respectively.
As the circle touches the two opposite sides, its diameter will be same as the breadth of the rectangle. Given, lb = 135 and
⇒
From this
∴ Required perimeter:
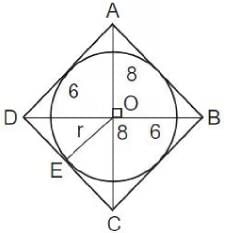
Q2: A circle is inscribed in a thombus with diagonals 12 cm and 16 cm. The ratio of the area of circle to the area of rhombus is [2020]
(a) 5π/18
(b) 6π/25
(c) 3π/25
(d) 2π/15
Ans: b
Sol:
Given the circle is inscribed in the rhombus of diagonals 12 and 16 . Let O be the point of intersection of the diagonals of the rhombus. Then, OE (radius) ⊥ DC.
Also
As area of ΔODC should be the same, we have, 1/2 x 6 x 8 = 6π/25
Q3: A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is [2020]
(a) 232
(b) 256
(c) 264
(d) 243
Ans: d
Sol: As the cone is cut at one-third height from the top (the vertex), the total volume is proportional to the cubes of the heights of the two parts.
Ratio of volumes two parts == 1 : 27
Hence the bottom part will have volume of 27 - 1 i.e., 26 parts.
Given ( 26 - 1) i.e., 25 parts -225 cc.
Hence the required answer is 27 parts = 27 x 255 / 25 = 243 cc.
Q4: From an interior point of an equilateral triangle, perpendiculars are drawn on all three sides. The sum of the lengths of the three perpendiculars is s. Then the area of the triangle is [2020]
(a) 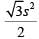
(b) 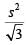
(c) 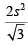
(d) 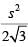
Ans: b
Sol:
PD + PE + PF = s
Area of =
As AB = BC = CA, we've
=
Now
⇒
Required Value =
Q5: The sum of the perimeters of an equilateral triangle and a rectangle is 90 cm. The area, T, of the triangle and the area, R, of the rectangle, both in sq cm, satisfy the relationship R = T2 . If the sides of the rectangle are in the ratio 1: 3, then the length, in cm, of the longer side of the rectangle, is [2020]
(a) 24
(b) 27
(c) 21
(d) 18
Ans: b
Sol: Let the breadth of the rectangle be b.
Length of the rectangle = 3b
Let a be the side of the equilateral triangle.
Given,
Given,
2(4b) + 3a = 90
⇒ 8 (a2 / 4) + 3a - 90 = 0
⇒ 2a2 + 3a - 90 = 0
⇒ (a - 6)(2a + 15) = 0
⇒ a = 6
∴ b = 9 ⇒ 3b = 27
Q6: Two circular tracks T1 and T2 of radii 100 m and 20 m, respectively touch at a point A. Starting from A at the same time, Ram and Rahim are walking on track T1 and track T2 at speeds 15 km/hr and 5 km/hr respectively. The number of full rounds that Ram will make before he meets Rahim again for the first time is [2020]
(a) 4
(b) 3
(c) 2
(d) 5
Ans: b
Sol: Time taken by each of them to complete one round
= Circumference of the circle / speed
Time taken for Ram to cover one round =
Time taken for Rahim to cover one round =
Time taken by Ram and Rahim meet each other for the first time = LCM of 48π and 28.8π = 144π
∴ Number of rounds made by Ram before he meets Rahim for the first time = 144π / 48π
= 3
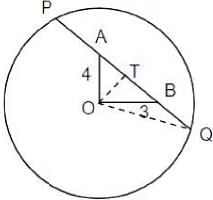
Q7: Let C be a circle of radius 5 meters having center at O. Let PQ be a chord of C that passes through points A and B where A is located 4 meters north of O and B is located 3 meters east of O. Then, the length of PQ, in meters, is nearest to [2020]
(a) 7.2
(b) 7.8
(c) 6.6
(d) 8.8
Ans: d
Sol:
OT = 2.4M
In ΔOTQ
OQ2 = OT2 + TQ2 ⇒ TQ2 = OQ2 - OT2
= (5)2 - (2.4)2
= 19.24
⇒
∴ PQ = 2TQ = 8.8m
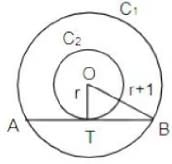
Q8: Let C1 and C2 be concentric circles such that the diameter of C1 is 2 cm longer than that of C2. If a chord of C1 has length 6 cm and is a tangent to C2, then the diameter, in cm, of C1 is [2020]
Ans: 10
Sol:
Given, d + 2 = D ⇒ r + 1 = R
In the figure OT = r and OB = r + 1
OT ⊥ AB as AB is the tangent
OT bisects AB i.e., TB = 6/2 = 3
Now, in ΔOTB, OT2 + TB2 = OB2
∴ r2 + 32 = (r + 1)2 ⇒ r = 4
∴ D = 2(R ) = 2(r + 1) = 10cm
Q9: Anil, Sunil, and Ravi run along a circular path of length 3 km, starting from the same point at the same time, and going in the clockwise direction. If they run at speeds of 15 km/hr, 10 km/hr, and 8 km/hr, respectively, how much distance in km will Ravi have run when Anil and Sunil meet again for the first time at the starting point? [2020]
(a) 4.2
(b) 5.2
(c) 4.8
(d) 4.6
Ans: c
Sol: Time taken by Anil and Sunil meet at the starting point
= 3/5
Distance run by Ravi in 3 / 5 hours = (3 / 5) x 8 = 24 / 5 = 4.8 km
Q10: In a trapezium ABCD, AB is parallel to DC, BC is perpendicular to DC and ∠BAD = 45° . If DC = 5 cm , BC= 4 cm, the area of the trapezium in sq cm is [2020]
Ans: 28
Sol: Dropping a perpendicular DE onto AB, the figure is divided into two parts - a rectangle of dimensions 4 x 5 and an isosceles triangle AED.
Required answer = Area of rectangle + Area of triangle = 4 x 5 + 1/2(4 x4) = 28cm2
2019
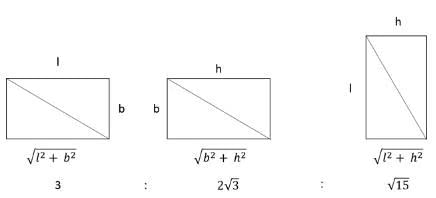
Q1: If the rectangular faces of a brick have their diagonals in the ratio 3 : 2 √3 : √15, then the ratio of the length of the shortest edge of the brick to that of its longest edge is [2019]
(a) 1 : √3
(b) 2 : √5
(c) √2 : √3
(d) √3 : 2
Ans: a
Sol:
From the given data, we know
l2 + b2 = 9k ...(1)
b2 + h2 = 12k ...(2)
l2 + h2 = 15k ...(3)
Adding (1) , (2) and (3) we get
2(l2 + b2 + h2) = 36 k
l2 + b2 + h2 = 18k ...(4)
Subtracting (1), (2) , (3) from (4) we get
h2 = 9k
l2 = 6k
b2 = 3k
Thus, ratio of shortest edge to longest edge = √3 : 3 = 1 : √3.
Q2: Corners are cut off from an equilateral triangle T to produce a regular hexagon H. Then, the ratio of the area of H to the area of T is [2019]
(a) 5 : 6
(b) 3 : 4
(c) 2 : 3
(d) 4 : 5
Ans: c
Sol:
Construct an Equilateral triangle and cut of equal lengths from all three sides. So we obtain a hexagon and three equilateral triangles of side 'a' in return.
We know that a hexagon comprises of 6 Equilateral Triangles. Since the side of the hexagon is also 'a', we obtain 6 equilateral triangles in return.
Thus, we have a total of 6 + 3 = 9 equilateral triangles of side 'a'
Ratio of area of Hexagon with Area of Triangle = 6: 9 = 2: 3
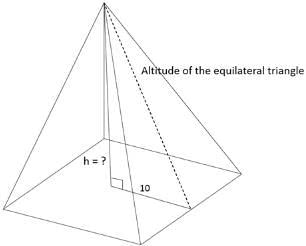
Q3: The base of a regular pyramid is a square and each of the other four sides is an equilateral triangle, length of each side being 20 cm. The vertical height of the pyramid, in cm, is [2019]
(a) 10√2
(b) 8√3
(c) 12
(d) 5√5
Ans: a
Sol:
It is given that the diagram is a square pyramid and all 4 sides of the triangle are of equal sides.
Now, we need to plug in a right triangle and apply Pythagoras theorem to find the vertical height of the triangle.
Draw a vertical from the apex of the pyramid and draw a line to the base along the equilateral triangle. Connect the points in the base to form a right triangle.
The hypotenuse would be the slant height of the pyramid, which is the altitude of the equilateral triangle.
Length of the base = 10 cms
Hypotenuse = Altitude of the equilateral triangle = (√3/2) x 20 = 10√3 cm
Therefore, (Vertical height)2 = (10√3)2 - 102 = 200
Vertical height = √200 = 10√2 cms
Q4: A man makes complete use of 405 cc of iron, 783 cc of aluminium, and 351 cc of copper to make a number of solid right circular cylinders of each type of metal. These cylinders have the same volume and each of these has radius 3 cm. If the total number of cylinders is to be kept at a minimum, then the total surface area of all these cylinders, in sq cm, is [2019]
(a) 1044(4 + π)
(b) 8464π
(c) 928π
(d) 1026(1 + π)
Ans: d
Sol: Calculation:
A man makes cylinder having equal volume by complete use of 405 cc of iron, 783 cc of aluminium, and 351 cc of copper.
Thus the number of cylinder is to be kept at a minimum,
Volume of each cylinder = HCF of 405, 783, 351 = 27
Then, the volume of each cylinder = 27
⇒ πr2h = 27
⇒ π × 32 × h = 27
⇒ h = 27/9π = 3/π
The volume of each cylinder = 27
The number of cylinder = (405/27) + (783/27) + (351/27)⇒ 15 + 29 + 13 = 57
The total surface area of cylinder = 2πrh + 2πr2
The total surface area of all the cylinder = 57 × [(2 × π × 3 × 3/π ) + 2 × π × 32]
⇒ 57 × [18 + 18π] = 1026(1 + π)
∴The total surface area of all the cylinder is 1026(1 + π).
2018
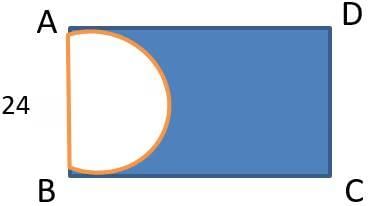
Q1: From a rectangle ABCD of area 768 sq cm, a semicircular part with diameter AB and area 72π sq cm is removed. The perimeter of the leftover portion, in cm, is [2018]
(a) 88 + 12π
(b) 80 + 16π
(c) 86 + 8π
(d) 82 + 24π
Ans: a
Sol: Given that ABCD be the rectangle of area of 768 sq cm. A semicircular part with diameter AB and area 72π sq cm is removed
From the area given we can find the radius r as
r2 = 144
r = 12 cm
The diameter AB is 24 since r = 12
So we have a rectangle ABCD
AB × BC = 768
24 × BC = 768
BC = 768/24
BC = 32
Now we have to find the perimeter of the left over portion (shaded area)
Perimeter = AD + DC + BC + 1/2 perimeter of the circle
Perimeter = 32 + 24 + 32 + 2πr/2 (r = 12 cm)
Perimeter = 88 + 12π cm
The perimeter of the leftover portion, in cm, is 88 + 12π
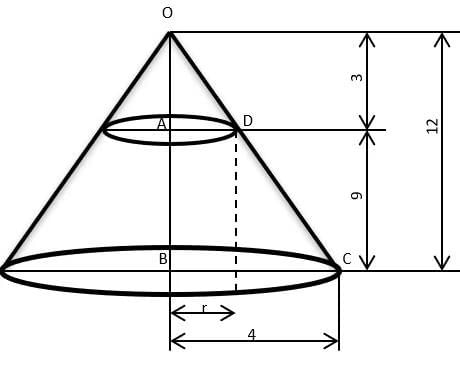
Q2: A right circular cone, of height 12 ft, stands on its base which has diameter 8 ft. The tip of the cone is cut off with a plane which is parallel to the base and 9 ft from the base. With π = 22/7, the volume, in cubic ft, of the remaining part of the cone is: [TITA 2018]
Ans: 198 cubic ft
Sol:
From the diagram, △OAD is similar to △OBC
Volume of the remaining part = Volume of OBC – Volume OAD
Volume of the remaining part = (1/3 x 22/7 x 4 × 4 × 12 ) - (1/3 x 22/7 x 1 × 1 × 3)
Volume of the remaining part = 22/7 x (64 − 1)
Volume of the remaining part = 198 cubic ft
Q3: In a parallelogram ABCD of area 72 sq cm, the sides CD and AD have lengths 9 cm and 16 cm, respectively. Let P be a point on CD such that AP is perpendicular to CD. Then the area, in sq cm, of triangle APD is [2018]
(a) 18√3
(b) 24√3
(c) 32√3
(d) 12√3
Ans: c
Sol:
Given Area (ABCD) = 72 sq cm, CD = 9cms, AD = 16cms
Area of Parallelogram = Base × Height
CD × 16 = 72
CD = (72/16) cms
We extend CD till P such that ∠APD = 90°
So, again by applying the area formula considering CD as base
CD × AP = Area of Parallelogram ABCD
9 × AP = 72
AP = 8 cms
We have AP = 8 cms, AD = 16 cms We observe that the ratio of the sides form a 1 : √3 : 2 triangle Therefore DP = 8√3 cms Area (△APD) = 1/2 × AD × DP = 1/2 × 8 × 8√3 sq cms Area (△APD) = 32 √3 sq cms
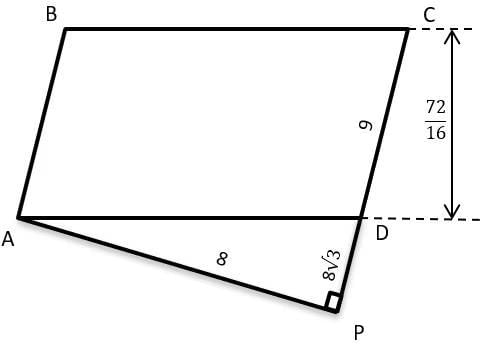
Q4: The area of a rectangle and the square of its perimeter are in the ratio 1 : 25. Then the lengths of the shorter and longer sides of the rectangle are in the ratio [2018]
(a) 3 : 8
(b) 2 : 9
(c) 1 : 4
(d) 1 : 3
Ans: c
Sol: Given that the area of a rectangle and the square of its perimeter are in the ratio 1: 25, we have to find the ratio of the lengths of the shorter and longer sides of the rectangle i.e. b : l
The area of the rectangle = lb
The square of its perimeter = [2(l + b)]2
⇒ lb : [2(l + b)]2 = 1 : 25
⇒ lb : 4[l2 + 2lb + b2] = 1 : 25
⇒ 25 lb = 4[l2 + 2lb + b2]
⇒ 25 lb = 4l2 + 8lb + 4b2
⇒ 4l2 - 17lb + 4b2 = 0
⇒ 4l2 - 16lb - lb + 4b2 = 0
⇒ 4l[l- 4b] – b [l- 4b] = 0
⇒ [l - 4b][4l - b] = 0
By this we can find that the ratio of the shorter and longer sides of the rectangle b : l is in the ratio 1: 4
In other way ,if we want to deal with only one variable and do not want to factorize divide this 4l2 - 17lb + 4b2 = 0 by l2 throughout
Since we have to find ratio of b : l, b/l can be substituted with x
4 - 17x + 4x2 = 0
Now x can be found by simplifying it
Q5: A parallelogram ABCD has area 48 sqcm. If the length of CD is 8 cm and that of AD is s cm, then which one of the following is necessarily true? [2018]
(a) s ≥ 6
(b) s ≠ 6
(c) 5 ≤ s ≤ 7
(d) s ≤ 6
Ans: a
Sol:
Given that a parallelogram ABCD has an area 48 sq cm. The length of CD is 8 cm and that of AD is s cm
Since the area given here is 48 sq.cm the height can be found as 6 sq.cm
We have to find which of the following options is necessarily true
Since this (shaded portion) is a right angled triangle with 6 as its height and s as its hypotenuse so we can assure that s ≥ 6 and s cannot be less than 6 so we can eliminate the other options.
By this we can come to the conclusion that s ≥ 6
2017
Q1: A solid metallic cube is melted to form five solid cubes whose volumes are in the ratio 1 : 1 : 8: 27: 27. The percentage by which the sum of the surface areas of these five cubes exceeds the surface area of the original cube is nearest to: [2017]
(a) 10
(b) 50
(c) 60
(d) 20
Ans: b
Sol: Given that a solid metallic cube is melted to form five solid cubes whose volumes are in the ratio 1 : 1 : 8 : 27 : 27. We have to find the percentage by which the sum of the surface areas of these five cubes exceeds the surface area of the original cube.
Let us take the volume of the 5 cubes to be 1x3 , 1x3 , 8x3 , 27x3 , 27x3
Volume of the original cube = x3(1 + 1 + 8 + 27 + 27)
Volume of the original cube = 64x3
Sides of the original cube = ∛64x3 = 4x
Similarly, sides of the 5 smaller cubes = x , x , 2x , 3x , 3x .
Surface Area of a cube = 6a2
Surface Area of the original cube = (4x) × (4x) = 16x2
Surface area of the smaller cubes = x2 , x2 , 4x2 , 9x2 , 9x2
Sum of the surface areas of the smaller cubes = x2(1 + 1 + 4 + 9 + 9) = 24x2
Change in surface area = 24x2 – 16x2 = 8x2
%change =
Hence the percentage by which the sum of the surface areas of these five cubes exceeds the surface area of the original cube is nearest to 50%.
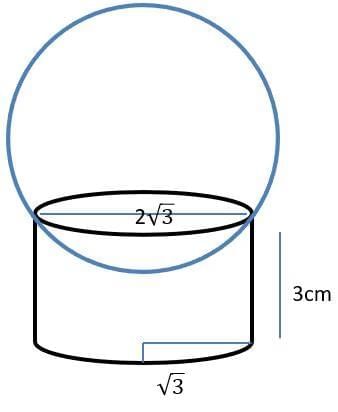
Q2: A ball of diameter 4 cm is kept on top of a hollow cylinder standing vertically. The height of the cylinder is 3 cm, while its volume is 9 π cm3. Then the vertical distance, in cm, of the topmost point of the ball from the base of the cylinder is: (TITA 2017)
Ans: 6
Sol:
Given that the height of the cylinder is 3 cm, while its volume is 9π cm3
Volume of the cylinder ⇒ πr2h = 9π cm3
r2 = 9 × 3 or r = √3
So the diameter is 2√3 cm
A ball of diameter 4 cm is kept on top of a hollow cylinder standing vertically.
Since OPQ is the right angled triangle
We can find the OP = 1 cm.
We have to find the vertical distance of the topmost point of the ball from the base of the cylinder.
Since OP = 1, to reach the topmost point still it has to go 2 cm from the point O.
The vertical distance, in cm, of the topmost point of the ball from the base of the cylinder is 2 + 1 + 3 = 6 cm
|
167 videos|229 docs|95 tests
|
FAQs on Mensuration CAT Previous Year Questions with Answer PDF
| 1. What are the key formulae used in mensuration for CAT preparation? |  |
| 2. How do I approach mensuration problems in the CAT exam? |  |
| 3. Are there any common mensuration topics asked in CAT? |  |
| 4. How can I improve my speed in solving mensuration questions for CAT? |  |
| 5. What strategies can I use to tackle difficult mensuration problems in CAT? |  |