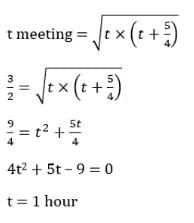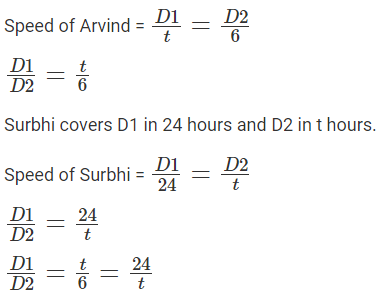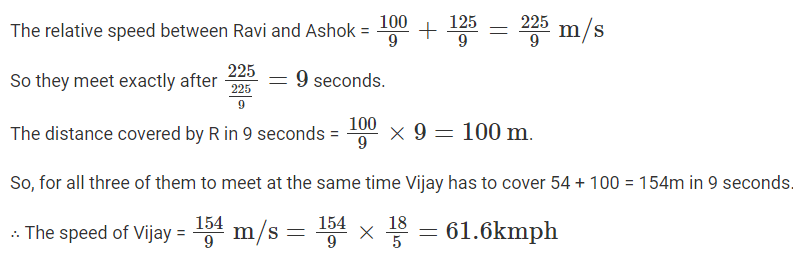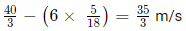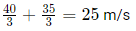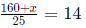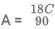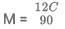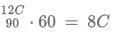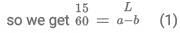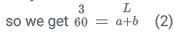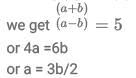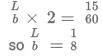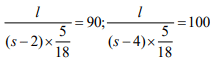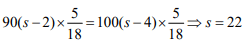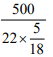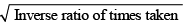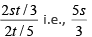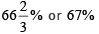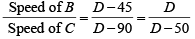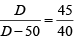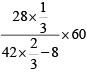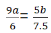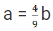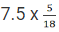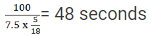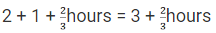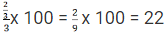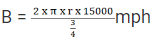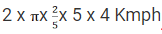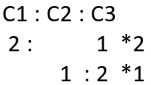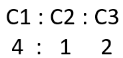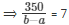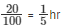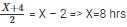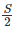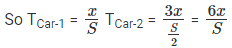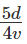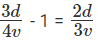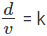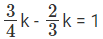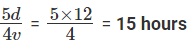Time & Distance CAT Previous Year Questions with Answer PDF

2024
Q1: Two places A and B are 45 kms apart and connected by a straight road. Anil goes from A to B while Sunil goes from B to A. Starting at the same time, they cross each other in exactly 1 hour 30 minutes. If Anil reaches B exactly 1 hour 15 minutes after Sunil reaches A, the speed of Anil, in km per hour, is
(a) 16
(b) 12
(c) 18
(d) 14
Ans: b
Sol: Let the speeds of Anil and Sunil be a and s respectively.
(a + s) × 1.5 = 45
⇒ a + s = 30 ... (i)Let the time taken by Sunil after crossing = t hours.
So, time taken by Anil = (t + 5/4) hours.
So, the time taken by Anil = 1 + 5/4 = 9/4 hour
Total time taken by Anil = 3/2 + 9/4
= 15/4 hoursHence, the speed of Anil = 45 ÷ (15/4) = 12
Q2: A bus starts at 9 am and follows a fixed route every day. One day, it traveled at a constant speed of 60 km per hour and reached its destination 3.5 hours later than its scheduled arrival time. Next day, it traveled two-thirds of its route in one-third of its total scheduled travel time, and the remaining part of the route at 40 km per hour to reach just on time. The scheduled arrival time of the bus is
(a) 7 pm
(b) 9 pm
(c) 10:30 pm
(d) 7:30 pm
Ans: (d)
Sol: Let the distance be d and scheduled time be t.
Speed = x / t
A.T.Q,
From (2), x = 80t, now putting this value in (1), we get
t = 10.5 hours
The scheduled arrive time = 9am + 10.5 hours = 7:30 PM.
2023
Q1: Brishti went on an 8-hour trip in a car. Before the trip, the car had travelled a total of x km till then, where x is a whole number and is palindromic, i.e., x remains unchanged when its digits are reversed. At the end of the trip, the car had travelled a total of 26862 km till then, this number again being palindromic. If Brishti never drove at more than 110 km/h , then the greatest possible average speed at which she drove during the trip, in km/h , was [2023]
(a) 90
(b) 100
(c) 80
(d) 110
Ans: (b)
Sol: The distance travelled before the trip (x in km.) is a palindrome.
Let the average speed of Brishti be s kmph.
The total distance covered by Brishti after the trip is 26862 km.
The distance covered by Brishti during the trip is 8×s = 8s km.
x = 26862 – 8s
For x to be a palindrome, of the given options, s can only be 100.
Therefore, the average speed of Brishti during the trip is 100 kmph.
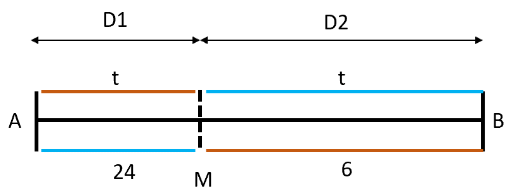
Q2: Arvind travels from town A to town B, and Surbhi from town B to town A, both starting at the same time along the same route. After meeting each other, Arvind takes 6 hours to reach town B while Surbhi takes 24 hours to reach town A. If Arvind travelled at a speed of 54 km/h, then the distance, in km, between town A and town B is [2023]
Sol:
Let the distance between city A and the meeting point M be D1 and the distance between city B and the meeting point M be D2.
Arvind covers D1 in t hours and D2 in 6 hours.t2 = 6 × 24 = 122
t = 12
Total time taken by Arvind to travel from city A to city B = (t + 6) = 18 hours.
Speed of Arvind = 54 kmph
Distance between city A to city B = 54 × 18 = 972 km.
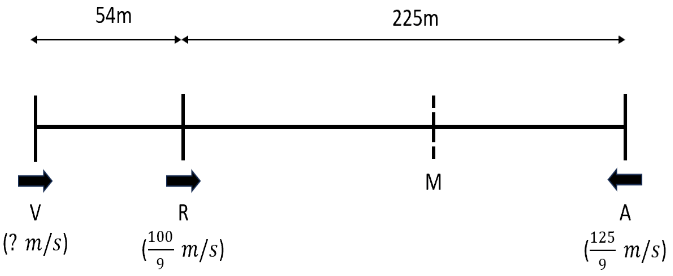
Q3: Ravi is driving at a speed of 40 km/h on a road. Vijay is 54 meters behind Ravi and driving in the same direction as Ravi. Ashok is driving along the same road from the opposite direction at a speed of 50 km/h and is 225 meters away from Ravi. The speed, in km/h, at which Vijay should drive so that all the three cross each other at the same time, is [2023]
(a) 58.8
(b) 64.4
(c) 67.2
(d) 61.6
Ans: (d)
Sol: The speeds of Ravi and Ashok converted to meters per second arerespectively.
Let M be the meeting point between Ravi and Ashok.
2022
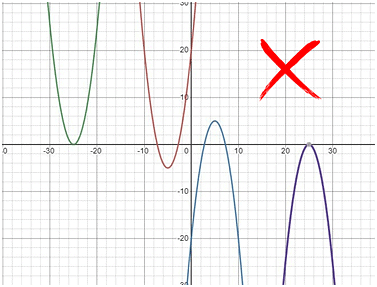
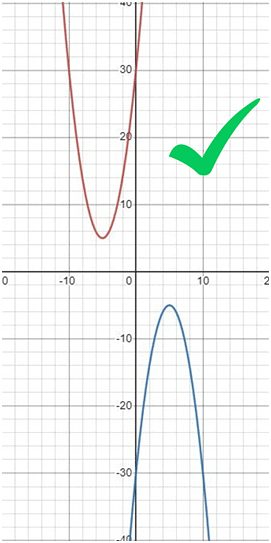
Q1: Let a, b, c be non-zero real numbers such that b2 < 4ac , and f(x) = ax2 + bx + c . If the set S consists of al integers m such that f(m) < 0 , then the set S must necessarily be [2022]
(a) the set of all integers
(b) either the empty set or the set of all integers
(c) the empty set
(d) the set of all positive integers
Ans: (b)
Sol: We are given the definition of the function, f(x) = ax2 + bx + c , and been told that b2<4ac . This means that f(x) has imaginary roots and therefore no real roots at all.
If a function has no real roots, the graph of the function can never touch the x-axis, because touching the x-axis means, for some real value x, the value of f(x) is 0. In other words, it means that the function has roots for some real value x.When we graph this function quadratic function f(x), we get a parabola, that should never touch the x-axis. Such a parabola should be completely above the x-axis or completely below the x-axis.
If it is completely above the x-axis:
It means that the value of f(x) is always positive for any value of x.
The set of values of x that satisfies the condition that f(x) < 0 is an empty set.
If it is completely below the x-axis:
It means that the value of f(x) is always negative for any value of x.
The set of values of x that satisfies the condition that f(x) < 0 is the set of all real numbers.
Since set S contains all the integers ‘m’ that satisfy the above conditions, Set S is either an empty set or the set of all integers.
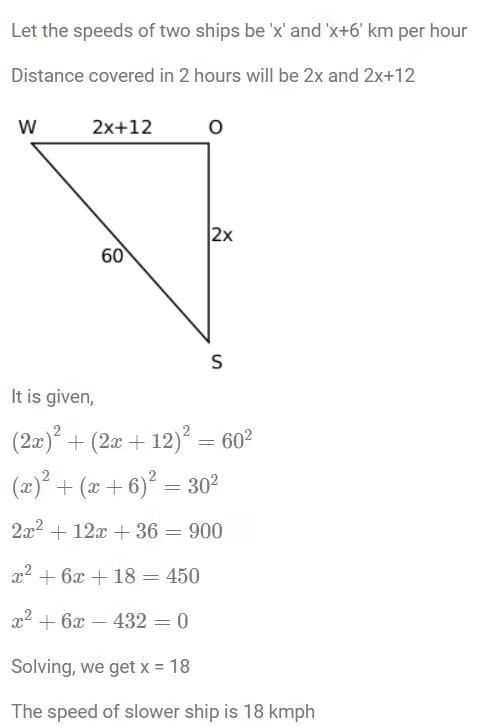
Q2: Two ships meet mid-ocean, and then, one ship goes south and the other ship goes west, both travelling at constant speeds. Two hours later, they are 60 km apart. If the speed of one of the ships is 6 km per hour more than the other one, then the speed, in km per hour, of the slower ship is
(a) 20
(b) 24
(c) 12
(d) 18
Ans: d
Sol:
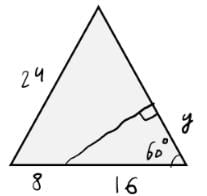
Q3: Two ships are approaching a port along straight routes at constant speeds. Initially, the two ships and the port formed an equilateral triangle with sides of length 24 km. When the slower ship travelled 8 km, the triangle formed by the new positions of the two ships and the port became right-angled. When the faster ship reaches the port, the distance, in km, between the other ship and the port will be
(a) 6
(b) 4
(c) 8
(d) 12
Ans: d
Sol:
cos 60 = y/16
=> y = 8
So, speeds of the two boats are in the ratio 1 : 2
When faster ship covers y = 8, slower ship would have covered 8/2 = 4 more i.e., 16-4 = 12 km away from the port.
Q4: Moody takes 30 seconds to finish riding an escalator if he walks on it at his normal speed in the same direction. He takes 20 seconds to finish riding the escalator if he walks at twice his normal speed in the same direction. If Moody decides to stand still on the escalator, then the time, in seconds, needed to finish riding the escalator is
Ans: 60
Let the normal speed of Moody be x steps/sec and speed of escalator be y steps/sec.
Length of escalator = (x+y)30 = (2x+y)20
=> 3x+3y = 4x+2y
=> x = y
If he decides to stand still, then x = 0 and time taken = Distance/spd = (x+y)30/y = (y+y)30/y = 60 seconds
Q5: Two cars travel from different locations at constant speeds. To meet each other after starting at the same time, they take 1.5 hours if they travel towards each other, but 10.5 hours if they travel in the same direction. If the speed of the slower car is 60 km/hr, then the distance traveled, in km, by the slower car when it meets the other car while traveling towards each other, is
(a) 100
(b) 90
(c) 120
(d) 150
Ans: b
Sol:
Speed of slower car = 60kmph
Let speed of faster car be x kmph
Let the distance between the two cars be y km.
y = 1.5(60 + x) ------(1)
y = 10.5(x - 60) -------(2)
(2)/(1)
=> 60 + x = 7(x – 60)
=> x = 80
y = 210 km
Ratio of speeds = 3/4
Distance covered by the slower car when it meets the faster car while traveling in the same direction = 3/(3+4) x 210 = 90 kms
2021
Q1: Two trains cross each other in 14 seconds when running in opposite directions along parallel tracks. The faster train is 160 m long and crosses a lamp post in 12 seconds. If the speed of the other train is 6 km/hr less than the faster one, its length, in m, is [2021]
(a) 184
(b) 192
(c) 190
(d) 180
Ans: (c)
Sol: Speed of the faster train = 160/12 = 40/3 m/s
Speed of the slower train =
Sum of speeds (when the trains travel towards each other) =
Let the slower train be xx metres long; then:
On solving, x = 190 m
Q2: Two trains A and B were moving in opposite directions, their speeds being in the ratio 5 : 3. The front end of A crossed the rear end of B 46 seconds after the front ends of the trains had crossed each other. It took another 69 seconds for the rear ends of the trains to cross each other. The ratio of length of train A to that of train B is [2021]
(a) 3 : 2
(b) 5 : 3
(c) 2 : 3
(d) 2 : 1
Ans: (a)
Sol: Considering the length of train A = La, length of train B = Lb.
The speed of train A be 5x, speed of train B be 3x.
From the information provided :
The front end of A crossed the rear end of B 46 seconds after the front ends of the trains had crossed each other.
In this case, train A traveled a distance equivalent to the length of train B which is Lb at a speed of 5x + 3x = 8x because both the trains are traveling in the opposite direction.
Hence (8x) x (46) = Lb.
In the information provided :
It took another 69 seconds for the rear ends of the trains to cross each other.
In the next 69 seconds
The train B traveled a distance equivalent to the length of train A in this 69 seconds.
Hence (8x) x (69) = La.
La/Lb = 69/46 = 3/2 = 3 : 2
Q3: Mira and Amal walk along a circular track, starting from the same point at the same time. If they walk in the same direction, then in 45 minutes, Amal completes exactly 3 more rounds than Mira. If they walk in opposite directions, then they meet for the first time exactly after 3 minutes. The number of rounds Mira walks in one hour is
Ans: 8
Sol: Considering the distance travelled by Mira in one minute = M, The distance traveled by Amal in one minute = A.
Given if they walk in the opposite direction it takes 3 minutes for both of them to meet.
Hence 3*(A+M) = C. (1) C is the circumference of the circle.
Similarly, it is mentioned that if both of them walk in the same direction Amal completes 3 more rounds than Mira :
Hence 45*(A-M) = 3C. (2)
Multiplying (1)*15 we have :
45A + 45M = 15C.
45A - 45M = 3C.
Adding the two we haveSubtracting the two
Since Mira travels
in one minute, in one hour she travels :
Hence a total of 8 rounds.
Alternatively,Let the length of track be L and velocity of Mira be a and Amal be b
Now when they meet after 45 minutes Amal completes 3 more rounds than Mira so we can say they met for the 3rd time moving in the same direction so we can say they met for the first time after 15 minutes
So we know Time to meet = Relative distance /Relative velocityNow When they move in opposite direction
They meet after 3 minutesDividing (1) and (2)
Now substituting in (1)
we get :So we can say 1 round is covered in 1/8 hours
so in 1-hour total rounds covered = 8.
2020
Q1: Two persons are walking beside a railway track at respective speeds of 2 and 4 km per hour in the same direction. A train came from behind them and crossed them in 90 and 100 seconds, respectively. The time, in seconds, taken by the train to cross an electric post is nearest to [2020]
(a) 87
(b) 82
(c) 75
(d) 78
Ans: (b)
Sol: Let the length of the train be l and its speed be s. Given
⇒
∴ Length of the train =500 m.
Hence the required time to cross a lamp post =
i.e. 81.81 (or) 82 sec.
Q2: A straight road connects points A and B. Car 1 travels from A to B and Car 2 travels from B to A, both leaving at the same time. After meeting each other, they take 45 minutes and 20 minutes, respectively, to complete their journeys. If Car 1 travels at the speed of 60 km/hr, then the speed of Car 2, in km/hr, is [2020]
(a) 90
(b) 100
(c) 80
(d) 70
Ans: (a)
Sol: In this particular case, we know Ratio of speeds =
C1 : C2 = √20 : 45 i.e., 2: 3
As the speed of Car C1 is 60 kmph, the speed of Car C2 is 90 kmph
Q3: A train travelled at one-thirds of its usual speed, and hence reached the destination 30 minutes after the scheduled time. On its return journey, the train initially travelled at its usual speed for 5 minutes but then stopped for 4 minutes for an emergency. The percentage by which the train must now increase its usual speed so as to reach the destination at the scheduled time, is nearest to [2020]
(a) 58
(b) 67
(c) 61
(d) 50
Ans: (b)
Sol: Let the usual speed of the train be s and time taken at that speed be 't'.
Given by travelling at s/3, it reached 30 min late. Hence the usual time:
Distance travelled = s x t
Distance travelled in the first 5min = s x t / 3. D
Distance to be travelled in the last 6min = 2 st / 3
Required speed to cover that distance on time =
Hence the percentage increase in its speed = (2 / 3) x 100
i.e.,
Q4: Leaving home at the same time, Amal reaches office at 10: 15 am if he travels at 8 km/hr, and at 9: 40 am if he travels at 15 km/hr. Leaving home at 9: 10 am, at what speed, in km/hr, must he travel so as to reach office exactly at 10 am? [2020]
(a) 13
(b) 14
(c) 12
(d) 11
Ans: (c)
Sol: Let the speed in the first two cases be s and the distance be "d'. Given,
d/8 - d/15 = 35/60 ⇒ d = 10km
Required speed = 10/50/60 = 12kmph
Q5: In a car race, car A beats car B by 45 km, car B beats car C by 50 km, and car A beats car C by 90 km. The distance (in km) over which the race has been conducted is [2020]
(a) 500
(b) 475
(c) 550
(d) 450
Ans: (d)
Sol: Let the length of the racetrack be D.
When A covers D km, B covers ( D -45) km and C covers (D-90) km
When B covers D km, C covers ( D -50) km
The ratio of the speeds of the racers is same as the ratio of the distance travelled in a given time period.
Ratio of speed of B and C is
⇒
⇒ 40D = 45D - 50 x 45
⇒ D = 450
Q6: Vimla starts for office every day at 9 am and reaches exactly on time if she drives at her usual speed of 40 km/hr. She is late by 6 minutes if she drives at 35 km/hr. One day, she covers two-thirds of her distance to office in one-thirds of her usual time to reach office, and then stops for 8 minutes. The speed, in km/hr, at which she should drive the remaining distance to reach office exactly on time is [2020]
(a) 29
(b) 27
(c) 28
(d) 26
Ans: (c)
Sol: Let the original time taken by Vimla be t minutes 40t / 60 = 35 x (t + 6) / 60
⇒ t = 35 x 6/5 = 42min
The distance to office =28 km
Required answer =
= 28 kmph
Q7: A and B are two railway stations 90 km apart. A train leaves A at 9:00 am, heading towards B at a speed of 40 km/hr. Another train leaves B at 10:30 am, heading towards A at a speed of 20 km/hr. The trains meet each other at [2020]
(a) 11 : 45 am
(b) 10 : 45 am
(c) 11 : 20 am
(d) 11 : 00 am
Ans: (d)
Sol: The distance travelled by A before B starts his journey = 40 x 1.5 = 60
The time taken by them to meet each other = 90-60 / 40+20 = 30/60 = 0.5 hours
Required answer =10: 30 a.m. +30 min =11: 00 a.m.
2019
Q1: A cyclist leaves A at 10 am and reaches B at 11 am. Starting from 10:01 am, every minute a motorcycle leaves A and moves towards B. Forty-five such motorcycles reach B by 11 am. All motorcycles have the same speed. If the cyclist had doubled his speed, how many motorcycles would have reached B by the time the cyclist reached B? [2019]
(a) 22
(b) 20
(c) 15
(d) 23
Ans: (c)
Sol: It is given that the cyclist starts at 10:00 am from A and reaches B at 11:00 am
Now, Motorcyclists start every minute from 10:01 am, and 45 such motorcyclists reach B before 11:00 am
If they leave one by one every minute, the 45th motorcyclist would have left by 10:45 am to reach B at 11:00 am.
Thus, time taken by one motorcyclist to reach B from A = 15 minutes.
Now, the cyclist doubles his speed. This means, he reaches B at 10:30 am
So, the last motorcyclist should have left A by 10:15 am
Thus, 15 motorcyclists would have reached B by the time the cyclist reaches B
Q2: John jogs on track A at 6 kmph and Mary jogs on track B at 7.5 kmph. The total length of tracks A and B is 325 metres. While John makes 9 rounds of track A, Mary makes 5 rounds of track B. In how many seconds will Mary make one round of track A? [2019]
Sol: Let the track length for John be 'a' and for Mary be 'b'
So, Distance travelled by John = 9a
Distance travelled by Mary = 5b
Now, Time taken by John =
Time taken by Mary =
We know that Time taken by John = Time taken by Mary
Total track length = 325 meters
So,= 325 meters
= 325 meters
b = 225 meters
a = 100 meters
Mary jogs at 7.5 Kmph =
So, time taken =
Q3: Two ants A and B start from a point P on a circle at the same time, with A moving clock-wise and B moving anti-clockwise. They meet for the first time at 10:00 am when A has covered 60% of the track. If A returns to P at 10:12 am, then B returns to P at [2019]
(a) 10:27 am
(b) 10:25 am
(c) 10:45 am
(d) 10:18 am
Ans: (a)
Sol: By the time A and B meet for the first time, A covers 60% of the distance, while B covers 40% of the distance.
So, the speeds of A and b are in the ratio 60:40 or 3:2
Hence, the time they take to cover a particular distance will be in the ratio 2:3
We know that A covers 60% of the distance at 10:00 AM and covers 100% of the distance at 10:12 AM.
That means A takes 12 minutes to cover 40% of the track. So to cover the entire track he must have taken 12+12+6 = 30 minutes.
(because 40% + 40% + 20% = 100%)
Since the time taken by A and B to complete the track are in the ratio 2:3, the time taken by B to complete the track will be 45 minutes.
At 10:00 AM, B has covered 40% of the track. If we can find out what time does B take to complete the remaining 60% of the track, we can find the finish time of B.
Time required to complete 60% of the track = 60% of 45 = 27 minutes.
Hence, B complete one single round at 10:27 AM.
Q4: Two cars travel the same distance starting at 10:00 am and 11:00 am, respectively, on the same day. They reach their common destination at the same point of time. If the first car travelled for at least 6 hours, then the highest possible value of the percentage by which the speed of the second car could exceed that of the first car is [2019]
(a) 20
(b) 10
(c) 35
(d) 25
Ans: (a)
Sol:The minimum time travelled by Car 1 = 6 hours.Minimum time travelled by Car 2 = 5 hours
Now, the time taken can be of any value -> (6,5) (7,6) ...... (1000,999)
However, since we want to calculate the highest possible percentage by which speed of car 2 could exceed car 1, we consider the lowest time taken - 6 hours and 5 hours, respectively.
Let the distance between the start and finish be 30 Kms (LCM of 6 and 5)
So, Car 1 travels at 5 Kmph and Car 2 travels at 6 Kmph
Percentage increase in speed by Car
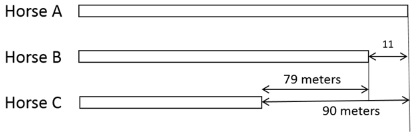
Q5: In a race of three horses, the first beat the second by 11 metres and the third by 90 metres. If the second beat the third by 80 metres, what was the length, in metres, of the racecourse? [2019]
Sol: 880 meters
A beats B by 11 meters. When B completes the 11 meters, there is a lead of 80 meters to C
So, C must have travelled only 90 - 80 = 10 meters
When B travels 11 meters, C travels only 10 meters
Ratio of distance travelled by second and third horse are11x and 10 x respectively
We know that the second horse beats the third horse by 80 meters.
So, Length of the track = Distance travelled by the second horse = 11 x 80 = 880 meters
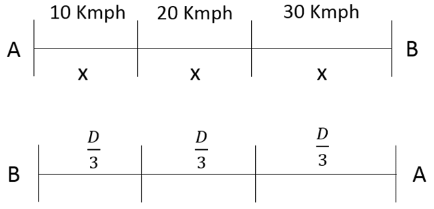
Q6: One can use three different transports which move at 10, 20, and 30 kmph, respectively. To reach from A to B, Amal took each mode of transport 1/3 of his total journey time, while Bimal took each mode of transport 1/3 of the total distance. The percentage by which Bimal’s travel time exceeds Amal’s travel time is nearest to [2019]
(a) 22
(b) 19
(c) 21
(d) 20
Ans: (a)
Sol:
Let the distance be = 60 Kms.
So, Bimal travels a distance of 20Kms in each mode and Amal travels 10, 20 and 30 Kms respectively in 1 hour each
Time taken by Bimal = Time taken to travel 20 kms in 10 Kmph + Time taken to travel 20 kms in 20 Kmph + Time taken to travel 20 kms in 30 Kmph
Time taken by Bimal =
Extra time taken by Bimal =
Percentage increase in time =
So, Percentage increase in time = 22
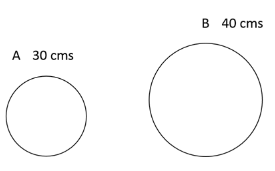
Q7: The wheels of bicycles A and B have radii 30 cm and 40 cm, respectively. While traveling a certain distance, each wheel of A required 5000 more revolutions than each wheel of B. If bicycle B traveled this distance in 45 minutes, then its speed, in km per hour, was [2019]
(a) 18π
(b) 16π
(c) 12π
(d) 14π
Ans: (b)
Sol:Circumference of A and B are in the ratio 3: 4
So, Ratio of Distance travelled in one revolution by A and B = 3: 4
Since they travel the same distance,
Ratio of number of revolutions of A and B = 4: 3 ----- (1)
We know that each wheel of A requires 5000 more revolutions than B
So, the Ratio of number of revolutions of A and B = (n + 5000): n ------(2)
So, comparing (1) and (2)
Number of revolutions of A and B are 20000 and 15000 respectively
So, we know Bike B does 15000 revolutions in 45 minutes
Distance travelled = 2 x π x r x Number of revolutions
Speed of Bike
Speed of Bike B =
Speed of Bike B = 16π Kmph
2018
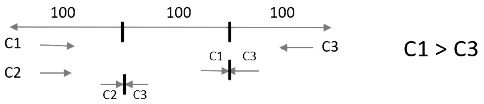
Q1: Points A, P, Q and B lie on the same line such that P, Q and B are, respectively, 100 km, 200 km and 300 km away from A. Cars 1 and 2 leave A at the same time and move towards B. Simultaneously, car 3 leaves B and moves towards A. Car 3 meets Car 1 at Q, and Car 2 at P. If each car is moving in uniform speed then the ratio of the speed of Car 2 to that of Car 1 is [2018]
(a) 1 : 4
(b) 2 : 9
(c) 1 : 2
(d) 2 : 7
Ans: (a)
Sol:
It is given that points A, P, Q and B lie on the same line such that P, Q and B are 100 km, 200 km and 300 km away from A. Let us draw the diagram first. All of them are on the same straight line and P, Q lie between A and B.
Cars 1 and Cars 2 leave A at the same time and move towards B. Simultaneously, Car 3 leaves B and moves towards A. Let us add more details to the diagram. C1 and C2 move towards B and C3 moves towards A. C3 meets C1 at Q and C3 meets C2 at P.
Let us assume the speeds of Car 1, 2, and 3 to be C1, C2 and C3 respectively. Car 1 is travelling quicker than Car 2. When Car 1 travels 200 km to reach Q, Car 3 has travelled 100 km or ratio of their speeds, C1 : C3 is 2 : 1.C1 and C2 move towards B and C3 moves towards A. C3 meets C1 at Q and C3 meets C2 at P.
Let us assume the speeds of Car 1, 2, and 3 to be C1, C2 and C3 respectively.When Car 3 travels 200 km to reach P, Car 2 has travelled 100 km or ratio of their speeds, C3 : C2 is 2 : 1. Now we have all the ratios. We know that C1 : C3 is 2 : 1 and C3 : C2 is 2 : 1. We can see that C3 is the common link
So, taking LCM of C3, we get,
We can see that ratio of speeds of Car 2 to Car 1 is 1 : 4. Hence, C2 : C1 = 1 : 4
Q2: On a long stretch of east-west road, A and B are two points such that B is 350 km west of A. One car starts from A and another from B at the same time. If they move towards each other, then they meet after 1 hour. If they both move towards east, then they meet in 7 hrs. The difference between their speeds, in km per hour, is [2018]
Sol: 50
Given that A and B are two points such that B is 350 km west of A. One car starts from A and another from B at the same time.
They meet after one hour or their relative velocity is (a + b)km/hr and their relative distance is 350kmswhich is equal to 350 kms/hr
If they both move towards east, then they meet in 7 hrs.
We have to find the difference between their speeds, in km per hour. B is catching upon A, so once again their relative distance will be 350kms.
Relative speed = b – a , B travels faster so that it can meet a.
⟹ b - a = 50 km/hr
We know that b + a = 350 km/hr
By this we can find the values of a and b but they have asked for only the difference between their speeds which is b – a = 50km/hr
Q3: Points A and B are 150 km apart. Cars 1 and 2 travel from A to B, but car 2 starts from A when car 1 is already 20 km away from A. Each car travels at a speed of 100 kmph for the first 50 km, at 50 kmph for the next 50 km, and at 25 kmph for the last 50 km. The distance, in km, between car 2 and B when car 1 reaches B is [2018]
Sol: 5
Given that points A and B are 150 km apart.
Cars 1 and 2 travel from A to B, but car 2 starts from A when car 1 is already 20 km away from A.
Each car travels at a speed of 100 kmph for the first 50 km, at 50 kmph for the next 50 km, and at 25 kmph for the last 50 km.
The Car 1 is 20km away from A and it travels at 100kmph and the time taken is
So car 2 is 12 minutes behind car 1.
We have to find the distance in km, between car 2 and B when car 1 reaches B.If car 1 reaches B, car 2 will take 12 minutes to reach b.
Distance between car 2 and B is 25 × 1/5 = 5 kms
The distance, in km, between car 2 and B when car 1 reaches B is 5 kms.
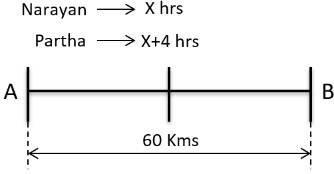
Q4: The distance from A to B is 60 km. Partha and Narayan start from A at the same time and move towards B. Partha takes four hours more than Narayan to reach B. Moreover, Partha reaches the mid-point of A and B two hours before Narayan reaches B. The speed of Partha, in km per hour, is [2018]
(a) 6
(b) 3
(c) 4
(d) 5
Ans: (d)
Sol:
Let Narayanan take X hrs to reach B then Partha would take X + 4 hrs
Its given that Partha reaches the mid-point of A and B two hours before Narayan reaches B
So, Partha would take 8+4 = 12 hrs to travel 60 Kms at a speed ofKmph
Speed of Partha = 5 Kmph
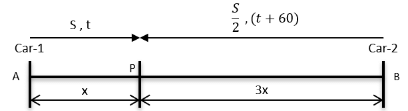
Q5: Point P lies between points A and B such that the length of BP is thrice that of AP. Car 1 starts from A and moves towards B. Simultaneously, car 2 starts from B and moves towards A. Car 2 reaches P one hour after car 1 reaches P. If the speed of car 2 is half that of car 1, then the time, in minutes, taken by car 1 in reaching P from A is: [2018]
Sol: 12
Let us take the distance AP = x and BP = 3x
It’s also given that SpeedCar-2 =SpeedCar-1
S1 = S S2 =
Car 2 takes one hour more than Car 1
T2 = t minutes T2 = (t + 60) minutes
We know that Time =
TCar-1 = t TCar-2 = 6t
We know, TCar-2 takes (t + 60) minutes
6t = t + 60
5t = 60
t = 12 minutes
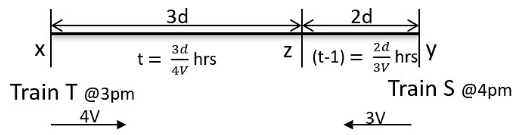
Q6: Train T leaves station X for station Y at 3 pm. Train S, traveling at three quarters of the speed of T, leaves Y for X at 4 pm. The two trains pass each other at a station Z, where the distance between X and Z is three-fifths of that between X and Y. How many hours does train T take for its journey from X to Y? [2018]
Sol:
From question, XZ = 3d, YZ = 2d
As their speeds are in ratio 4:3
Let their speeds be 4V and 3V
Time (T to reach Z) =hrs ....(1)
Time (S to reach Z) =hrs ....(2)
We need to find the time taken for T To travel from X to Y
Time =
Train S started one hour late than Train T
⇒
Let
k = 12
So,
|
167 videos|229 docs|95 tests
|
FAQs on Time & Distance CAT Previous Year Questions with Answer PDF
| 1. How is time and distance related in CAT exams? |  |
| 2. What are some common formulas used in time and distance problems in CAT exams? |  |
| 3. How can candidates improve their speed in solving time and distance problems for CAT exams? |  |
| 4. What are some tips for effectively solving time and distance questions in CAT exams? |  |
| 5. How important is the concept of relative speed in time and distance problems for CAT exams? |  |