SSC CGL Exam > SSC CGL Notes > General Intelligence and Reasoning for SSC CGL > Calculate Cube Roots
Calculate Cube Roots | General Intelligence and Reasoning for SSC CGL PDF Download
Introduction
- We have heard many people saying that there is actually no shortcut to find the cube root of a number. This is not true. In fact, there are ways to quickly, easily and accurately calculate the cube root of a given number.
- These ways when mastered can help you to get the cube root of a number in less than 5 seconds.
- We are now going to have a look at the simplest & fastest way of calculating the cube root of a number in this article.

Calculating the Cube Root of a number quickly and accurately
- The first and the most important step is to memorize the cubes of 1 to 20. These would form an important part of your toolkit in solving the cube roots. Here is a table for your convenience.

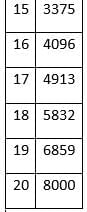
- Once you memorize this list, the next step is to remember the last digit (unit digit) of each of these cubes. Here is the list again, only with unit digits this time.
1 → 1
2 → 8
3 → 7
4 → 4
5 → 5
6 → 6
7 → 3
8 → 2
9 → 9
0 → 0 - That’s it. Now that you have memorized the cubes of first 9 natural numbers and their unit digits, you are all set to amaze your friends by calculating cube roots within 5 seconds.
Shortcut Method (5-Second Trick)
- Split the numberinto two parts:
- Last 3 digits
- Remaining digits
- Find the largest cube less than or equal to the first part.
- That gives the tens digit.
- Look at the last digitof the number.
- Match it with cube endings to get the ones digit.
- Combine both digits → Cube root.
Let us see how to calculate cube roots in less than 5 seconds.
Q.1. Find out the cube root of 50653.
Here is how to solve this question:
- The first step is to divide the number into 2 parts by separating the last 3 digits. So, we get 50 & 563 as the two parts of the number.
- Now, take the first part and find the largest cube contained in the first part i.e. in 50 = 27 (which is the cube of 3). The next cube i.e. 64 (cube of 4) is larger than 50. Now, as 27 is the cube of 3, your ten’s part of cube root would be 3. [This is why we memorized the cubes]
- The next step is to take the last digit of the number, which in this case is 3. Which number’s cube had 3 as the unit digit? 7… right?? (7*7*7=343) Hence, 7 is the unit digit of your solution. [This is why we memorized the endings]
- So, your answer is 37. Try cubing 37 on a calculator to verify your answer.
Let us solve another example to show how the answer can be achieved in less than 5 seconds.
Q.2. Calculate the cube root of 941192.
By Step 1: We get two parts i.e. 941 and 192.
By Step 2: The largest cube less than 941 is 729 (cube of 9). So, ten’s digit is 9.
By Step 3: The ending digit is 2. Hence, unit’s digit is 8. That’s it. 98 is the answer.
Practice it a bit and you would be able to solve this in even less than 5 seconds.
The document Calculate Cube Roots | General Intelligence and Reasoning for SSC CGL is a part of the SSC CGL Course General Intelligence and Reasoning for SSC CGL.
All you need of SSC CGL at this link: SSC CGL
|
177 videos|210 docs|199 tests
|
FAQs on Calculate Cube Roots - General Intelligence and Reasoning for SSC CGL
| 1. How do you calculate cube roots? |  |
Ans. To calculate the cube root of a number, you can use the following steps:
1. Identify the number whose cube root you want to find.
2. Make an estimate of the cube root that is close to the actual value.
3. Divide the number by the estimate and obtain a new estimate of the cube root.
4. Repeat step 3 until the estimate becomes accurate enough.
| 2. Can I use a calculator to calculate cube roots? |  |
Ans. Yes, most calculators have a cube root function that allows you to directly calculate the cube root of a number. Simply enter the number and press the cube root button (∛) to obtain the result.
| 3. What is the cube root of a negative number? |  |
Ans. The cube root of a negative number is also a negative number. For example, the cube root of -8 is -2, as (-2) x (-2) x (-2) equals -8. In general, the cube root of a negative number will always have the same sign as the original number.
| 4. Can you calculate the cube root of a fraction? |  |
Ans. Yes, you can calculate the cube root of a fraction. Simply calculate the cube root of the numerator and the cube root of the denominator separately. For example, to find the cube root of 1/8, you would calculate the cube root of 1 (which is 1) and the cube root of 8 (which is 2). Therefore, the cube root of 1/8 is 1/2.
| 5. Are there any shortcuts or formulas for calculating cube roots? |  |
Ans. Yes, there is a shortcut method called the "prime factorization method" that can be used to calculate cube roots. This method involves finding the prime factorization of the number and then grouping the factors in sets of three. The cube root is then obtained by taking one factor from each group. However, this method is more suitable for larger numbers and may not be practical for smaller numbers.
Related Searches

















