Year 5 Exam > Year 5 Notes > Year 5 Mathematics > Calculating angles around a point
Calculating angles around a point | Year 5 Mathematics PDF Download
What is a full turn?
- A full turn around a point is 360°. Angles around a point always sum to 360°.
- Knowing one of the angles allows you to calculate the other angles around the point, often without needing a protractor.
Examples
Example: 1
This diagram shows that there are two angles to be found.
What are angles C and D?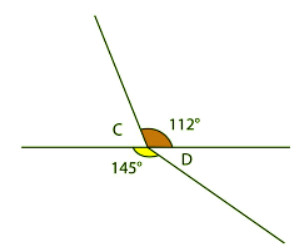 The angles either side of the straight line must add up to 180°.
The angles either side of the straight line must add up to 180°.
To find angle C, you can subtract 112° from 180°.
180° - 112° = 68°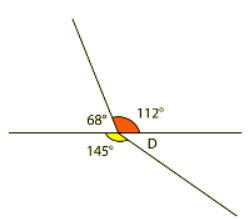 Angle C is 68°.
Angle C is 68°.
To find angle D, subtract 145° from 180°.
180° - 145° = 35°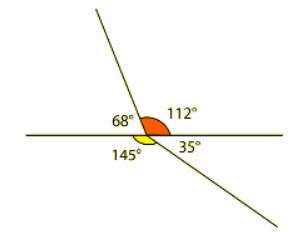 Angle D is 35°.
Angle D is 35°.
Example: 2
What is the value of A? These two angles are around a point. They must add up to 360°.
These two angles are around a point. They must add up to 360°.
135° + A = 360°
We can rearrange this to find angle A:
A = 360° - 135°
Therefore:
360° - 135° = 225°
Angle A is 225°. However, sometimes you need to find more than one angle around a point.
However, sometimes you need to find more than one angle around a point.
The document Calculating angles around a point | Year 5 Mathematics is a part of the Year 5 Course Year 5 Mathematics.
All you need of Year 5 at this link: Year 5
|
45 videos|42 docs|11 tests
|
FAQs on Calculating angles around a point - Year 5 Mathematics
| 1. What is a full turn in terms of angles? |  |
Ans. A full turn refers to an angle of 360 degrees, which takes you back to the starting point after completing a full rotation around a point.
| 2. How is a full turn calculated when measuring angles around a point? |  |
Ans. To calculate a full turn when measuring angles around a point, you simply need to add up all the angles that make up the rotation, which will total 360 degrees.
| 3. Why is understanding a full turn important in geometry and trigonometry? |  |
Ans. Understanding a full turn is crucial in geometry and trigonometry as it helps in visualizing angles around a point and determining the relationships between different angles within a circle.
| 4. How can angles around a point be used in real-life applications or problem-solving scenarios? |  |
Ans. Angles around a point can be used in real-life applications such as navigation, architecture, and engineering, where precise measurements and calculations of angles are necessary.
| 5. What are some common misconceptions people have about a full turn and angles around a point? |  |
Ans. Some common misconceptions include confusing a full turn with a half turn (180 degrees) and assuming that angles around a point always start and end at the same position.

|
Explore Courses for Year 5 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
















