Calculus and Approximation | Mathematics for EmSAT Achieve PDF Download

In mathematics, differential calculus is a branch of mathematics that deals with the process of finding the derivative of a function. It is the study of the rate of change of quantities with respect to other variables. The process of finding the derivative of the given function is called the differentiation. The concept of differential calculus is basically about cutting something into smaller pieces to find the rate of change. In general, if an equation involves the derivative of the dependent variable with respect to the independent variable, then it is called the differential equation.
dy/dx = f(x)
In this case, “x” is an independent variable and “y” is a dependent variable.

Generally, the derivatives are used to determine the followings:

• It is used to find the rate of change of quantities.
• It is used to find the equation of a tangent and a normal to a curve at a point.
• It is used to find the turning point on the graph function, which helps to locate the point where the largest or smallest value of the function occurs.
• It is used to find the intervals where the function is increasing or decreasing.
• It is used to find the approximate value of certain quantities.

For example, find the rate of change of the area of a circle per second with respect to the radius, when r is 5 cm.
We know that the area of a circle is A = πr². 
Therefore, the rate of change of area with respect to the radius is given by:
dA/dr = (d/dr)( πr²) 
dA/dr = 2πr
When r = 5 cm, then it becomes
dA/dr = 10π
Hence, the area of a circle is changing at the rate of 10π cm²/s.

Differential Calculus Approximations

Now, let us have a look at the differentials which are used to approximate certain quantities. Let a function f in x be defined such that f: D →R, D ⊂ R. Let y = f(x). Let a small increase in x be denoted by ∆x. If x increases by ∆x then the corresponding increase in y is given by ∆y = f(x + ∆x) – f(x) as shown in the figure given below.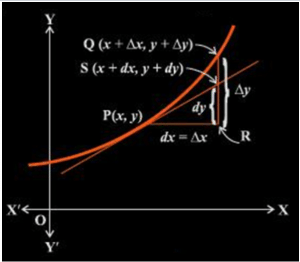 

Based on the above discussion, we can define the following:

• The differential of x which is represented as dx is given by dx = ∆x.
• Differential of y which is represented as dy is given by dy = f’(x)dx = (dy/dx) ∆x.

If in case the differential of x or dx = ∆x is comparatively very insignificant in comparison to x then dy is a good approximation of ∆y and dy ≈ ∆y. 
From the above discussion, it can be observed that differential of the independent variable is equal to the increase in the variable, but on the other hand, the differential of the dependent variable is not equal to the increase of the variable.
Let us look into the examples to have a better insight.

Approximation Examples

Example 1: Approximate √25.5 using differential.
Solution: Let us consider y = √x, where x = 25 and ∆x = 0.5. Then,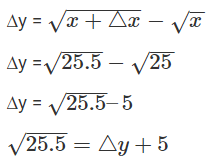

Since dy is approximately equal to ∆y, therefore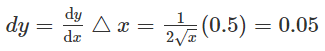

Therefore, the approximate value of √25.5 = 5 + 0.05 = 5.05

Example 2: Find the approximate value of the function f(3.02), where f(x) is given as 3x²+5x+3.
Solution:
Given that, f(x) = 3x²+5x+3
Assume x = 3, and ∆x = 0.02.
Hence, we can write the given function as:
f (3. 02) = f (x + ∆x) = 3(x + ∆x)² + 5(x + ∆x) + 3
We know that,
∆y = f (x + ∆x) – f (x). 

The above expression can be written as
f (x + ∆x) = f (x) + ∆y
As, dx = ∆x, it can be approximately written as f (x) + f ′(x) ∆x
Hence, f (3.02) ≈ (3x² + 5x + 3) + (6x + 5) ∆x
Now, substitute the values of x and ∆x, we get
= (3(3)² + 5(3) + 3) + (6(3) + 5) (0.02) 
Now, simplify it to get the approximate value
= (27 + 15 + 3) + (18 + 5) (0.02)
= 45 + 0.46 
= 45.46
Therefore, the approximate value of f(3.02) is 45.46.