This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Caselets (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Read the information carefully and answer the question.
Three companies L, M and N participated for campus recruitment in college Z. All the three companies selected an equal number of candidates. There were 60 candidates who were selected by L and M both. The number of candidates selected by both M and N was 68 less than twice the number of candidates selected by both L and M. There were 28 candidates who got placed in all the 3 companies. This number was 50% less than the number of candidates selected by both L and N. The total number of candidates selected by both L and N was 91.88% less than total number of candidates selected by all the three company.
Q. How many candidates were selected by company L?
Explanation
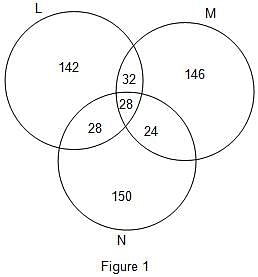
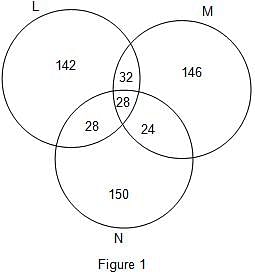
The Venn diagram for the given problem is as given in figure 1.
Firstly, there are 28 candidates placed in all the 3 companies.
So, 28 goes into the common region.
Then, 60 candidates were selected by both L and M.
So, 60 - 28 = 32 goes into the region common only to L and M.
Now, number of candidates selected by both M and N was 68 less than twice the number of candidates selected by both L and M.
Thus, number of candidates selected by both M and N = 2 × 60 - 68 = 120 - 68 = 52
Thus, 52 - 28 = 24 goes into the region common to both M and N.
Now, number of candidates selected by both L and N = 2 × 28 = 56
Thus, 56 - 28 = 28 goes into the region common to both L and N.
Now, let the total number of candidates selected = T
Number of candidates selected by both L and N = 56
So, 56 = T(1 - 0.9188) or T = 690
As equal number of candidates were selected by the 3 companies, the number of candidates in each company = 690/3 = 230
Thus, 230 - (32 + 28 + 28) = 230 - 88 = 142 goes into the region exclusive to L.
230 - (28 + 28 + 24) = 230 - 80 = 150 goes into the region exclusive to N.
230 - (32 + 28 + 24) = 230 - 84 = 146 goes into the region exclusive to M.
So, number of candidates selected by company L = 230
Hence, answer option (2) is correct.
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Read the information carefully and answer the question.
Three companies L, M and N participated for campus recruitment in college Z. All the three companies selected an equal number of candidates. There were 60 candidates who were selected by L and M both. The number of candidates selected by both M and N was 68 less than twice the number of candidates selected by both L and M. There were 28 candidates who got placed in all the 3 companies. This number was 50% less than the number of candidates selected by both L and N. The total number of candidates selected by both L and N was 91.88% less than total number of candidates selected by all the three company.
Q. Find the total number of candidates who were selected only by company L or M.
Explanation
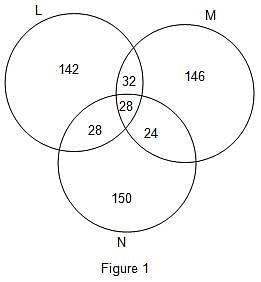
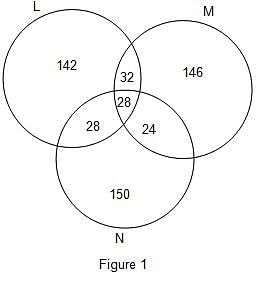
The Venn diagram for the given problem is as given in figure 1.
Firstly, there are 28 candidates placed in all the 3 companies.
So, 28 goes into the common region.
Then, 60 candidates were selected by both L and M.
So, 60 - 28 = 32 goes into the region common only to L and M.
Now, number of candidates selected by both M and N was 68 less than twice the number of candidates selected by both L and M.
Thus, number of candidates selected by both M and N = 2 × 60 - 68 = 120 - 68 = 52
Thus, 52 - 28 = 24 goes into the region common to both M and N.
Now, number of candidates selected by both L and N = 2 × 28 = 56
Thus, 56 - 28 = 28 goes into the region common to both L and N.
Now, let the total number of candidates selected = T
Number of candidates selected by both L and N = 56
So, 56 = T(1 - 0.9188) or T = 690
As equal number of candidates were selected by the 3 companies, the number of candidates in each company = 690/3 = 230
Thus, 230 - (32 + 28 + 28) = 230 - 88 = 142 goes into the region exclusive to L.
230 - (28 + 28 + 24) = 230 - 80 = 150 goes into the region exclusive to N.
230 - (32 + 28 + 24) = 230 - 84 = 146 goes into the region exclusive to M.
From the Venn diagram, it is clear that number of candidates selected by only L or M = Number of candidates selected by L or M and not by N = 142 + 32 + 146 = 320
Hence, answer option (3) is correct.
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Read the information carefully and answer the question.
Three companies L, M and N participated for campus recruitment in college Z. All the three companies selected an equal number of candidates. There were 60 candidates who were selected by L and M both. The number of candidates selected by both M and N was 68 less than twice the number of candidates selected by both L and M. There were 28 candidates who got placed in all the 3 companies. This number was 50% less than the number of candidates selected by both L and N. The total number of candidates selected by both L and N was 91.88% less than total number of candidates selected by all the three company.
Q. What is the total number of candidates who were placed in exactly two companies only?
Explanation
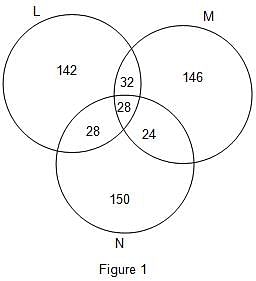
The Venn diagram for the given problem is as given in figure 1.
Firstly, there are 28 candidates placed in all the 3 companies.
So, 28 goes into the common region.
Then, 60 candidates were selected by both L and M.
So, 60 - 28 = 32 goes into the region common only to L and M.
Now, number of candidates selected by both M and N was 68 less than twice the number of candidates selected by both L and M.
Thus, number of candidates selected by both M and N = 2 × 60 - 68 = 120 - 68 = 52
Thus, 52 - 28 = 24 goes into the region common to both M and N.
Now, number of candidates selected by both L and N = 2 × 28 = 56
Thus, 56 - 28 = 28 goes into the region common to both L and N.
Now, let the total number of candidates selected = T
Number of candidates selected by both L and N = 56
So, 56 = T(1 - 0.9188) or T = 690
As equal number of candidates were selected by the 3 companies, the number of candidates in each company = 690/3 = 230
Thus, 230 - (32 + 28 + 28) = 230 - 88 = 142 goes into the region exclusive to L.
230 - (28 + 28 + 24) = 230 - 80 = 150 goes into the region exclusive to N.
230 - (32 + 28 + 24) = 230 - 84 = 146 goes into the region exclusive to M.
From the Venn diagram, it is clear that total number of candidates placed in exactly 2 companies only = 32 + 28 + 24 = 84
Hence, answer option (3) is correct.
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Study the given information and answer the following question.
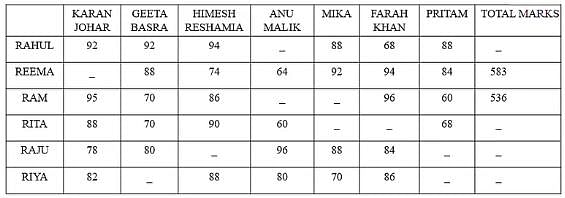
A talent hunt competition was being conducted by a TV Channel. As they were expecting variations in the type of talent, they appointed 7 different judges: Karan Johar, Geeta Basra, Himesh Reshamia, Anu Malik, Mika, Farah Khan and Pritam. In the first round, 6 contestants namely Rahul, Reema, Ram, Rita, Raju and Riya appeared before the panel for selection. Accidentally, the organisers forgot to mention the marks for which they were to be evaluated; therefore, each of the judges evaluated the contestants on a different total marks. The total marks for which the judges evaluated all the contestant were 100, 150, 50, 125, 150, 50 and 75 in the exact order of judges as mentioned above, respectively. The table mentioned below presents the percentage score of the contestants by each of the judges.
Q. What is the ratio of the total marks obtained by Rita from Karan Johar, Geeta Basra and Anu Malik to the total marks obtained by Rahul from Pritam, Mika and Farah Khan?
Explanation
Marks obtained by Rita from Karan Johar, Geeta Basra and Anu Malik = 88% of 100 + 70% of 150 + 60% of 125 = 88 + 105 + 75 = 268
Marks obtained by Rahul from Pritam, Mika and Farah Khan = 88% of 75 + 88% of 150 + 68% of 50 = 66 + 132 + 34 = 232
Required ratio = 268 : 232 = 67 : 58
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Study the given information and answer the following question.
A talent hunt competition was being conducted by a TV Channel. As they were expecting variations in the type of talent, they appointed 7 different judges: Karan Johar, Geeta Basra, Himesh Reshamia, Anu Malik, Mika, Farah Khan and Pritam. In the first round, 6 contestants namely Rahul, Reema, Ram, Rita, Raju and Riya appeared before the panel for selection. Accidentally, the organisers forgot to mention the marks for which they were to be evaluated; therefore, each of the judges evaluated the contestants on a different total marks. The total marks for which the judges evaluated all the contestant were 100, 150, 50, 125, 150, 50 and 75 in the exact order of judges as mentioned above, respectively. The table mentioned below presents the percentage score of the contestants by each of the judges.
Q. If the total marks given by Geeta and Pritam to Riya are one mark less than marks granted to Rahul by Geeta and Himesh, then what is the overall percentage of marks obtained by Riya?
Explanation
From the table we can find out that the percentage of marks obtained by Riya from Geeta and Pritam is missing.
So, assume the marks obtained by Riya from these two judges to be x + y.
Marks obtained by Rahul from Geeta and Himesh = 92% of 150 + 94% of 50 = 138 + 47 = 185
As per the statement, x + y + 1 = 185, so x + y = 184
Total marks obtained by Riya = 82% of 100 + x + 88% 50 + 80% of 125 + 70% of 150 + 86% of 50 + y
= 82 + x + 44 + 100 + 105 + 43 + y
= 374 + x + y
= 374 + 184
= 558
Therefore, overall percentage of marks obtained by Riya = (558 x 100)/700 = 79.71%
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Study the given information carefully to answer the question that follows:
In a college, there are 2400 students studying in different branches - Electronics, Mechanical, Electrical, IT, and Computer Science. The ratio of the number of boys to that of girls is 5 : 3. 12% boys study in the Electronics branch. 24% girls study in the Mechanical branch. The ratio of the number of boys to that of girls in the Electronics branch is 6 : 11. One-ninth of girls study in the Computer Science branch. 42% boys study in the IT branch. The number of girls studying in the IT branch is 10% of the boys studying in the same branch. The remaining girls study in the Electrical branch. The total number of students studying in the Computer Science branch is 285. 22% boys study in the Electrical branch. The remaining boys study in the Mechanical branch.
Q. What percentage of the total girls in the college do the girls in the IT branch constitute?
Explanation
Total number of students = 2400
Ratio of the number of boys to that of girls = 5 : 3
Number of boys = (5/8) × 2400 = 1500
Number of girls = (3/8) × 2400 = 900
42% boys studying in the IT branch = 42% of 1500 = 630
The number of girls in studying IT is 10% of the boys studying in the same branch = 10% of 630 = 63
Suppose x% of the total girls in the college are studying in the IT branch.
63 = x% of 900
x = 7
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Study the given information carefully to answer the question that follows:
In a college, there are 2400 students studying in different branches - Electronics, Mechanical, Electrical, IT, and Computer Science. The ratio of the number of boys to that of girls is 5 : 3. 12% boys study in the Electronics branch. 24% girls study in the Mechanical branch. The ratio of the number of boys to that of girls in the Electronics branch is 6 : 11. One-ninth of girls study in the Computer Science branch. 42% boys study in the IT branch. The number of girls studying in the IT branch is 10% of the boys studying in the same branch. The remaining girls study in the Electrical branch. The total number of students studying in the Computer Science branch is 285. 22% boys study in the Electrical branch. The remaining boys study in the Mechanical branch.
Q. The number of boys studying in the Mechanical branch is approximately what percentage of the total number of boys in the college?
Explanation
Total number of students = 2400
Ratio of the number of boys to that of girls = 5 : 3
Number of boys = (5/8) × 2400 = 1500
Number of girls = (3/8) × 2400 = 900
12% boys studying in Electronics = 12% of 1500 = 180
24% girls studying in Mechanical = 24% of 900 = 216
Ratio of the number of boys to that of girls in Electronics = 6 : 11
Number of girls studying in Electronics = 11 × 30 = 330 [Number of boys studying in Electronics = 180]
One-ninth of girls studying in Computer Science = (1/9) × (900) = 100
42% boys studying in IT = 42% of 1500 = 630
The number of girls studying in IT is 10% of the boys studying in the same branch = 10% of 630 = 63
The remaining girls are studying in Electrical = 900 - (216 + 330 + 100 + 63) = 191
Total number of students studying in Computer Science = 285
Number of boys studying in Computer science branch = 285 - 100 = 185
22% boys studying in Electrical = 22% of (1500) = 330
Number of boys studying in Mechanical = 1500 - (180 + 630 + 185 + 330) = 175
Suppose the number of boys studying in Mechanical is y percentage of the total number of boys in the college.
175 = y% of 1500
y = 11.66 or 11.67%
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Read the following information and answer the question that follows.
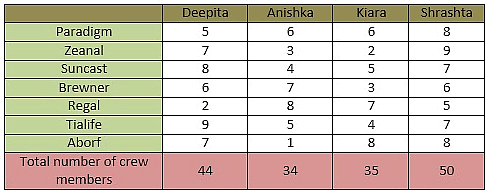
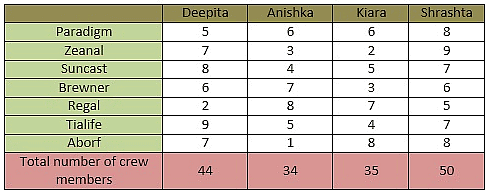
Four actresses - Deepita, Anishka, Kiara and Shrashta have dedicated some of their crew members to look after their public relations image in some top news agencies - Paradigm, Zeanal, Suncast, Brewner, Regal, Tialife and Aborf.
- Not more than 9 crew members are dedicated to one agency by any actress.
- Deepita and Shrashta have dedicated the greatest number of crew members an actress can send to Tialife and Zeanal, respectively.
- Anishka, Kiara and Shrashta have dedicated 4, 5 and 2 members less than the number of crew members dedicated by Deepita to Tialife.
- Sum of crew members of Deepita dedicated to Tialife and to Suncast is 17.
- Number of crew members of Anishka dedicated to Regal, Kiara dedicated to Aborf and Shrashta dedicated to Paradigm as well as to Aborf is the same as the number of crew members of Deepita dedicated to Suncast.
- Number of crew members of Shrashta dedicated to Tialife and to Suncast is the same and the number of crew members of Shrashta dedicated to Suncast and to brewner are consecutive numbers.
- Number of crew members of Deepita, Anishka, Kiara and Shrashta dedicated to Brewner, Paradigm, Paradigm and Brewner, respectively is the same.
- Sum of crew members of Shrashta dedicated to Brewner and to Regal is 11.
- Shrashta has the greatest number of crew members dedicated to news agencies, while Deepita has 6 less and Kiara has 15 less.
- Number of crew members dedicated by Shrashta to Regal is the same as the number of crew members of Kiara dedicated to Suncast and of Deepita dedicated to Paradigm.
- Deepita has 7 members each, dedicated both to Zeanal and to Aborf.
- Anishka has 10 crew members less than Deepita.
- Crew members of Deepita dedicated to Aborf are the same as the crew members of Anishka dedicated to Brewner.
- Anishka has 3 and 4 members dedicated to Zeanal and to Suncast, respectively. Kiara has 2 and 7 members dedicated to Zeanal and to Regal, respectively.
- Number of crew members of Deepita dedicated to Regal is not the same as the number of crew numbers of Anishka dedicated to Aborf.
Q. What is the sum of crew members of all actresses that are dedicated to Suncast and to Tialife?
Explanation
Tabulating the given information, we get
Sum of crew members of all actresses that are dedicated to Tialife and to Suncast = 8 + 4 + 5 + 7 + 9 + 5 + 4 + 7
Total crew members dedicated to Tialife and to Suncast = 49
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Read the following information and answer the question that follows.
Four actresses - Deepita, Anishka, Kiara and Shrashta have dedicated some of their crew members to look after their public relations image in some top news agencies - Paradigm, Zeanal, Suncast, Brewner, Regal, Tialife and Aborf.
- Not more than 9 crew members are dedicated to one agency by any actress.
- Deepita and Shrashta have dedicated the greatest number of crew members an actress can send to Tialife and Zeanal, respectively.
- Anishka, Kiara and Shrashta have dedicated 4, 5 and 2 members less than the number of crew members dedicated by Deepita to Tialife.
- Sum of crew members of Deepita dedicated to Tialife and to Suncast is 17.
- Number of crew members of Anishka dedicated to Regal, Kiara dedicated to Aborf and Shrashta dedicated to Paradigm as well as to Aborf is the same as the number of crew members of Deepita dedicated to Suncast.
- Number of crew members of Shrashta dedicated to Tialife and to Suncast is the same and the number of crew members of Shrashta dedicated to Suncast and to brewner are consecutive numbers.
- Number of crew members of Deepita, Anishka, Kiara and Shrashta dedicated to Brewner, Paradigm, Paradigm and Brewner, respectively is the same.
- Sum of crew members of Shrashta dedicated to Brewner and to Regal is 11.
- Shrashta has the greatest number of crew members dedicated to news agencies, while Deepita has 6 less and Kiara has 15 less.
- Number of crew members dedicated by Shrashta to Regal is the same as the number of crew members of Kiara dedicated to Suncast and of Deepita dedicated to Paradigm.
- Deepita has 7 members each, dedicated both to Zeanal and to Aborf.
- Anishka has 10 crew members less than Deepita.
- Crew members of Deepita dedicated to Aborf are the same as the crew members of Anishka dedicated to Brewner.
- Anishka has 3 and 4 members dedicated to Zeanal and to Suncast, respectively. Kiara has 2 and 7 members dedicated to Zeanal and to Regal, respectively.
- Number of crew members of Deepita dedicated to Regal is not the same as the number of crew numbers of Anishka dedicated to Aborf.
Q. What is the sum of crew members of Deepita, Kiara and Shrashta that are dedicated to Regal?
Explanation
Tabulating the given information, we get
Sum of crew members of Deepita, Kiara and Shrashta dedicated to Regal = 2 + 7 + 5
Crew members of Deepita, Kiara and Shrashta dedicated to Regal = 14
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Answer the question on the basis of the information given below.
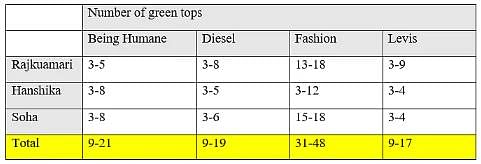
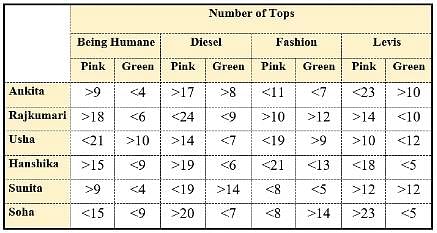
Anisha has a big collection of tops. The top with her is of one or the other of the four brands namely Being Humane, Diesel, Fashion and Levis. The colour of the tops with her is either pink or green. Out of the tops with her, Anisha has bought only a few of them whereas the rest are gifted to her by one or the other of her six friends namely Ankita, Rajkumari, Usha, Hanshika, Sunita and Soha. Anisha does not know the exact number of tops gifted to her but she knows that the number of green tops of each brand gifted to her by each of her mentioned friends is at least 3 and at most 18. Further, the number of pink tops of each brand gifted to her by each of his mentioned friends is at least 7 and at most 25.
Anisha asked her boyfriend to help her determine the number of tops gifted to her by each of her mentioned friends. In turn, her boyfriend provided her with the information listed in the table given below:
Q. Out of the green tops gifted to Anisha by Rajkumari, Hanshika and Soha, the number of green tops of brand 'Being Humane' is definitely less than the number of green tops of brand:
Explanation
The following table lists down the range of the total number of green tops of each brand gifted to Anisha by her mentioned friends:
Since, the maximum possible number of green tops of brand 'Being Humane' gifted to Anisha is less than the minimum possible number of green tops of brand 'Fashion' gifted to Anisha, therefore the number of green tops of brand 'Being Humane' gifted to Anisha is definitely less than the number of green tops of brand 'Fashion' gifted to Anisha.
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Answer the question on the basis of the information given below.
Anisha has a big collection of tops. The top with her is of one or the other of the four brands namely Being Humane, Diesel, Fashion and Levis. The colour of the tops with her is either pink or green. Out of the tops with her, Anisha has bought only a few of them whereas the rest are gifted to her by one or the other of her six friends namely Ankita, Rajkumari, Usha, Hanshika, Sunita and Soha. Anisha does not know the exact number of tops gifted to her but she knows that the number of green tops of each brand gifted to her by each of her mentioned friends is at least 3 and at most 18. Further, the number of pink tops of each brand gifted to her by each of his mentioned friends is at least 7 and at most 25.
Anisha asked her boyfriend to help her determine the number of tops gifted to her by each of her mentioned friends. In turn, her boyfriend provided her with the information listed in the table given below:
Q.. Let the number of tops of brand 'Being Humane' gifted to Anisha by Soha be 'X' and the number of tops of brand 'Fashion' gifted to Anisha by Usha be 'Y'. If Y > 3 × X, then which of the following can be a value of 'X'?
Explanation
Minimum possible value of X = 7 + 3 = 10
Maximum possible value of X = 14 + 8 = 22
Minimum possible value of Y = 7 + 10 = 17
Maximum possible value of Y = 18 + 18 = 36
It is given that Y > 3 × X, therefore the possible values of X are 10 and 11.
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Read the following information carefully to answer the question given thereafter.
5500 candidates from four different cities A, B, C and D have cleared the bank exam. 500 male candidates from city A have cleared the exam. The number of male candidates who cleared the exam from city C is % less than that of male candidates who cleared the exam from city D. The total number of candidates who cleared the exam from city A is 250 less than the total number of candidates who cleared the exam from city B. The ratio of number of female students from city C who have cleared the exam to the total number of students from city D who have cleared the exam is 16 : 31. The total number of candidates who have cleared the exam from city D is 100 less than 3 times the number of female candidates from city A who have cleared the exam. 650 female candidates from city D have cleared the exam. The number of female candidates from cities A, B, C and D who have cleared the exam is 100 less than number of male candidates from cities A, B, C and D who have cleared the exam. The number of male candidates who cleared the exam from city B is 20% more than number of male candidates who cleared the exam from city A.
Q. How many candidates from city B have cleared the exam?
Explanation
Let number of male candidates from city C who have cleared the exam = 8x
Let number of female candidates from city C who have cleared the exam = 16z
Let total number of candidates from city A who have cleared the exam = y
Total number of candidates from city B who have cleared the exam = y + 250
Number of candidates from city D who have cleared the exam = 31z
The following table can be drawn as per the given information:
The total number of female candidates from all 4 cities who have cleared the exam is 100 less than the number of male candidates from all cities who have cleared the exam.
Let total number of female candidates from all 4 cities who have cleared the exam = a
Total number of male candidates from all 4 cities who have cleared the exam = a + 100
So,
a + a + 100 = 5500
a = 2700
a + 100 = 2800
Also,
500 + 600 + 8x + 9x = 2800
17x = 1700
x = 100
9x + 650 = 31z
Since x = 100,
z = 50
y = 1050
So, the table can be redrawn as follows:
Hence, total number of candidates from city B who have cleared the exam = 1300
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Read the following information carefully to answer the question given thereafter.
5500 candidates from four different cities A, B, C and D have cleared the bank exam. 500 male candidates from city A have cleared the exam. The number of male candidates who cleared the exam from city C is % less than that of male candidates who cleared the exam from city D. The total number of candidates who cleared the exam from city A is 250 less than the total number of candidates who cleared the exam from city B. The ratio of number of female students from city C who have cleared the exam to the total number of students from city D who have cleared the exam is 16 : 31. The total number of candidates who have cleared the exam from city D is 100 less than 3 times the number of female candidates from city A who have cleared the exam. 650 female candidates from city D have cleared the exam. The number of female candidates from cities A, B, C and D who have cleared the exam is 100 less than number of male candidates from cities A, B, C and D who have cleared the exam. The number of male candidates who cleared the exam from city B is 20% more than number of male candidates who cleared the exam from city A.
Q. How many candidates from city B have cleared the exam?
Q. What percent candidates from city C were selected out of the total number of candidates selected from cities A, B, C and D?
Explanation
Let number of male candidates from city C who have cleared the exam = 8x
Let number of female candidates from city C who have cleared the exam = 16z
Let total number of candidates from city A who have cleared the exam = y
Total number of candidates from city B who have cleared the exam = y + 250
Number of candidates from city D who have cleared the exam = 31z
The following table can be drawn as per the given information:
The total number of female candidates from all 4 cities who have cleared the exam is 100 less than the number of male candidates from all cities who have cleared the exam.
Let total number of female candidates from all 4 cities who have cleared the exam = a
Total number of male candidates from all 4 cities who have cleared the exam = a + 100
So,
a + a + 100 = 5500
a = 2700
a + 100 = 2800
Also,
500 + 600 + 8x + 9x = 2800
17x = 1700
x = 100
9x + 650 = 31z
Since x = 100,
z = 50
y = 1050
So, the table can be redrawn as follows:
Total number of candidates selected from cities A, B, C and D = 5500
Percent of candidates selected from city C = 1600 × (100/5500) = 29.1%
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Read the information carefully and answer the question.
Three companies L, M and N participated for campus recruitment in college Z. All the three companies selected an equal number of candidates. There were 60 candidates who were selected by L and M both. The number of candidates selected by both M and N was 68 less than twice the number of candidates selected by both L and M. There were 28 candidates who got placed in all the 3 companies. This number was 50% less than the number of candidates selected by both L and N. The total number of candidates selected by both L and N was 91.88% less than total number of candidates selected by all the three company.
Q. How many candidates were selected by only company M?
Explanation
The Venn diagram for the given problem is as given in figure 1.
Firstly, there are 28 candidates placed in all the 3 companies.
So, 28 goes into the common region.
Then, 60 candidates were selected by both L and M.
So, 60 - 28 = 32 goes into the region common only to L and M.
Now, number of candidates selected by both M and N was 68 less than twice the number of candidates selected by both L and M.
Thus, number of candidates selected by both M and N = 2 × 60 - 68 = 120 - 68 = 52
Thus, 52 - 28 = 24 goes into the region common to both M and N.
Now, number of candidates selected by both L and N = 2 × 28 = 56
Thus, 56 - 28 = 28 goes into the region common to both L and N.
Now, let the total number of candidates selected = T
Number of candidates selected by both L and N = 56
So, 56 = T(1 - 0.9188) or T = 690
As equal number of candidates were selected by the 3 companies, the number of candidates in each company = 690/3 = 230
Thus, 230 - (32 + 28 + 28) = 230 - 88 = 142 goes into the region exclusive to L.
230 - (28 + 28 + 24) = 230 - 80 = 150 goes into the region exclusive to N.
230 - (32 + 28 + 24) = 230 - 84 = 146 goes into the region exclusive to M.
From the Venn diagram, it is obvious that number of candidates selected by only company M = 146
Hence, answer option (2) is correct.
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Read the information carefully and answer the question.
Three companies L, M and N participated for campus recruitment in college Z. All the three companies selected an equal number of candidates. There were 60 candidates who were selected by L and M both. The number of candidates selected by both M and N was 68 less than twice the number of candidates selected by both L and M. There were 28 candidates who got placed in all the 3 companies. This number was 50% less than the number of candidates selected by both L and N. The total number of candidates selected by both L and N was 91.88% less than total number of candidates selected by all the three company.
Q. What is the total number of candidates who were placed in exactly one company only?
Explanation
The Venn diagram for the given problem is as given in figure 1.
Firstly, there are 28 candidates placed in all the 3 companies.
So, 28 goes into the common region.
Then, 60 candidates were selected by both L and M.
So, 60 - 28 = 32 goes into the region common only to L and M.
Now, number of candidates selected by both M and N was 68 less than twice the number of candidates selected by both L and M.
Thus, number of candidates selected by both M and N = 2 × 60 - 68 = 120 - 68 = 52
Thus, 52 - 28 = 24 goes into the region common to both M and N.
Now, number of candidates selected by both L and N = 2 × 28 = 56
Thus, 56 - 28 = 28 goes into the region common to both L and N.
Now, let the total number of candidates selected = T
Number of candidates selected by both L and N = 56
So, 56 = T(1 - 0.9188) or T = 690
As equal number of candidates were selected by the 3 companies, the number of candidates in each company = 690/3 = 230
Thus, 230 - (32 + 28 + 28) = 230 - 88 = 142 goes into the region exclusive to L.
230 - (28 + 28 + 24) = 230 - 80 = 150 goes into the region exclusive to N.
230 - (32 + 28 + 24) = 230 - 84 = 146 goes into the region exclusive to M.
From the Venn diagram, it is clear that total number of candidates placed in exactly one company = 142 + 146 + 150 = 438
Hence, answer option (1) is correct.
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Read the given information carefully and answer the following questions.
A and B invested in a business in the ratio 4 : 5. A invested for 4 months more than B. At the end of year, the total profit earned is Rs. 35000 out of which B earned Rs. 15000.
Explanation
Let the amount invested by A and B be 4x and 5x respectively
Let B invested by ‘t’ months
Time of investment of A = t + 4
Profit ratio = 4x × (t + 4) : 5x × t = (4t + 16) : 5t
Now, B’s share:
5t/(4t + 16 + 5t) × 35000 = 15000
35t = 27t + 48
8t = 48
t = 6 months
Period of investment: A = 10 months, B = 6 months
∴ Required ratio = 10 : 6 = 5 : 3
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Read the following information carefully and answer the given questions:-
In school, the total number of students is 14,000. On the annual function of the school, 25% of the total boys and 60% of total girls have participated and the number of total girls in the school is equal to the number of boys who have not participated in the function.
Q. Find the number of boys who have participated in annual function of the school.
Explanation
Given:
Total number of students = 14,000
Percentage of boys who participated in annual function = 25%
Percentage of girls who participated in annual function = 60%
Number of girls in school = Number of boys who have not participated in function
Concept used:
Total number of boys or girls = Number of those who participated + Number of those who have not participated
Calculation:
Let the number of boys and girls be x and y respectively
Number of boys who have participated in annual function = 25% of x
⇒ 0.25x
Number of boys who have not participated = (x – 0.25x)
⇒ 0.75x
Number of girls in school = y = 0.75x
Now, as per the question
⇒ x + y = 14,000
⇒ x + 0.75x = 14,000
⇒ 1.75x = 14,000
⇒ x = 8000
Number of boys who have participated in annual function = 0.25x
⇒ 0.25 × 8000
⇒ 2000
∴ The number of boys who have participated in annual function is 2000
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Consider the following information and answer the questions based on it
In a group of 75 students, 12 like only cabbage, 15 like only cauliflower, 21 like only carrot, 12 like both carrot and cabbage, 13 like only capsicum and 2 like both capsicum and cauliflower.
Q. The difference between the people who like carrot and cauliflower is
A. 6
B. 18
C. 16
D. 4
Explanation
Total number of people who like carrot = 21 + 12 = 33
Total number of people who like cauliflower = 15 + 2 = 17
∴ Required difference = 33 – 17 = 16
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Read the given information carefully and answer the following questions.
Three streams Arts, Science, and Commerce are offered in 3 colleges A, B, and C.
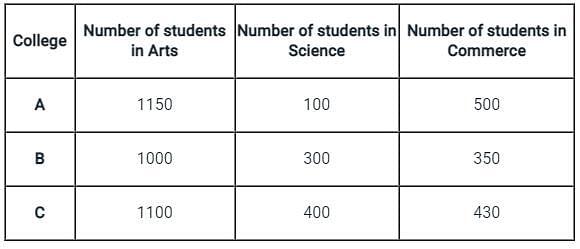
(i) There are 1750 students in college A. The number of Commerce students in college A is 400 more than that of in Science in college A. the ratio of the number of students in college A in Arts and Science is 23 : 2.
(ii) There are 3250 students in Arts in all colleges. The number of students in Science in all colleges is 37.5% less than that of in Commerce in all colleges.
(iii) The number of Arts students in college C is 10% more than that of in college B. the ratio of the number of students in Science in college B to that of in college C is 3 : 4.
(iv) The number of students in Commerce in college B is 30% less than that in college A. total number of students in college B is 280 less than that of in college C.
Q. The total number of students in college B is what percent more/less than that of in Science in all colleges?
Explanation
Let the number of students in Arts and Science in college A be 23x and 2x respectively.
⇒ Number of students in Commerce in college A = 400 + 2x
23x + 2x + 400 + 2x = 1750
27x = 1350
x = 50
College A: Arts = 1150, Science = 100, Commerce = 500
Let the number of Commerce students in all colleges be 8y
⇒ Number of Science students in all colleges = 62.5/100 × 8y = 5y
Number of students in Commerce in college B = 70/100 × 500 = 350
⇒ Number of students in Commerce in college C = 8y – (500 + 350)
⇒ 8y – 850
Let the number of students in Arts in college B be z
⇒ Number of students in Arts in college C = 110/100 × z = 1.1z
1150 + z + 1.1z = 3250
2.1z = 2100
z = 1000
Number of students in Science in college B = 3/7 × (5y – 100) = 15y/7 – 300/7
Number of students in Science in college C = 4/7 × (5y – 100) = 20y/7 – 400/7
Now, Total number of students in college B = 1000 + 350 + 15y/7 – 300/7
⇒ 1350 – 300/7 + 15y/7
Total number of students in college C = 1100 + 20y/7 – 400/7 + 8y – 850
⇒ 250 – 400/7 + 20y/7 + 8y
Now, 250 – 400/7 + 20y/7 + 8y – 280 = 1350 – 300/7 + 15y/7
⇒ 1380 + 100/7 = 61y/7
⇒ y = 160
Now, putting the value of y and z, we get
Total students in college B = 1000 + 300 + 350 = 1650
Total students in Science in all colleges = 100 + 300 + 400 = 800
∴ Required percent = (1650 – 800)/800 × 100 = 106.25%
Report a problem
Question for Practice Questions Level 2: Caselets - 2
Try yourself:Directions: Read the data carefully and answer the question.
Mr. ‘A’ type Different number of Words per Day. He worked for four days. The number of words typed by him on three different days: Monday, Tuesday, and Wednesday are in the ratio 3 : 4 : 2. Also number of words typed by Mr. ‘A’ on Sunday is 30% of the total words typed in four days. The no. of words typed by Mr. ‘A’ on Wednesday is 560.
Q. Find difference between total words type by Mr. ‘A’ on Sunday & Wednesday.
Explanation
Let total number of word type by Mr. A in four days = x
The number of words type by Mr. A in Sunday = x × 30/100 = 0.3x
The number of words type by Mr. A in Monday = (x – 0.3x) × 3/9 = 0.7x/3
The number of words type by Mr. A in Tuesday = (x – 0.3x) × 4/9 = 2.8x/9
The number of words type by Mr. A in Wednesday = (x – 0.3x) × 2/9 = 1.4x/9
Given that,
1.4x/9 = 560
⇒ x = 560 × 9/1.4 = 3600
The number of words type by Mr. A in Sunday = 0.3x = 0.3 × 3600 = 1080
The number of words type by Mr. A in Wednesday = 560 (Given)
So, required difference = 1080 – 560 = 520
Report a problem
% less than that of male candidates who cleared the exam from city D. The total number of candidates who cleared the exam from city A is 250 less than the total number of candidates who cleared the exam from city B. The ratio of number of female students from city C who have cleared the exam to the total number of students from city D who have cleared the exam is 16 : 31. The total number of candidates who have cleared the exam from city D is 100 less than 3 times the number of female candidates from city A who have cleared the exam. 650 female candidates from city D have cleared the exam. The number of female candidates from cities A, B, C and D who have cleared the exam is 100 less than number of male candidates from cities A, B, C and D who have cleared the exam. The number of male candidates who cleared the exam from city B is 20% more than number of male candidates who cleared the exam from city A.
