Cauchy-Euler Equation | Engineering Mathematics - Civil Engineering (CE) PDF Download

Introduction

The Cauchy-Euler Equation plays a significant role in the theory of linear differential equations because of its direct application to Fourier’s method in deconstructing PDE’s (partial differential equations). Let’s learn how to write the Cauchy-Euler equation and how to solve various types of Cauchy-Euler equations.

Cauchy-Euler Equation General Form

The differentiation equation gives the Cauchy-Euler differential equation of order n as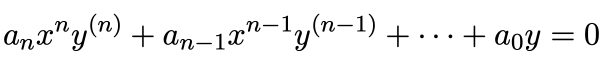

Here, a_i; i = 1, 2, 3,…, n are constants and a_n ≠ 0.

Second Order Cauchy-Euler Equation

The second-order Cauchy-Euler equation is of the form: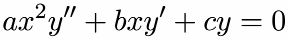
or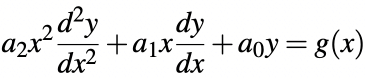

When g(x) = 0, then the above equation is called the homogeneous Cauchy-Euler equation.
In mathematics, the most commonly used Cauchy-Euler equation is the second-order Cauchy-Euler equation.

Cauchy-Euler Equation Examples

Below are a few examples of Cauchy-Euler equations of a different order.

• x² y′′ − 9xy′ + 25y = 0
• y′′ + 9y = sec 3x
• x²y′′ + 4y = 0
• x³ y′′′ − 6x² y′′ + 19xy′ − 27y = 0

How to Solve the Cauchy-Euler Differential Equation?

Go through the steps given below to understand the method of solving the second order Cauchy-Euler differential equation.
Step 1: Let us assume that y = y(x) = x^r be the solution of a given differentiation equation, where r is a constant to be determined.
Step 2: Fill the above formula for y in the differential equation and simplify. That means replace y with x^r.
Step 3: Solve the obtained polynomial equation for r.
Step 4: For each obtained value of r, x^r is a solution to the actual Euler equation.
If there is only one value for r, then y₁(x) = x^r is one solution to the differential equation, and we can reach the general solution by reducing order.
If there are two different real values for r, i.e., r₁ and r₂, then x^r1, x^r2 will be the fundamental set of solutions, whereas the general solution to the differential equation is y(x) = c₁x^r1 + c₂x^r2.

Cauchy-Euler Equation Solved Problems

Q.1. Solve: x² y′′ − 6xy′ – 18y = 0

Given second order Cauchy-Euler equation is:

x² y′′ − 6xy′ – 18y = 0
Let y = x^r and substitute in the given differential equation.
x² y′′ − 6xy′ – 18y = 0
x²[ xr ]′′ – 6x[ x^r ]′ – 18( x^r ) = 0
x² [r(r − 1)x^r−2] − 6x [r x^r−1] – 18x^r = 0
(r² − r)x^r − 6r x^r – 18x^r = 0

(r² – r – 6r – 18)x^r = 0
⇒ r² – 7r – 18 = 0
⇒ r² + 2r – 9r – 18 = 0
⇒ r(r + 2) – 9(r + 2) = 0
⇒ (r + 2)(r – 9) = 0
⇒ r = -2, r = 9
So, r = -2 and 9 are the two distinct possible values of r.

Therefore, the set of fundamental solution is {x^-2, x⁹} and the general solution is y = c₁x^-2 + c₂x⁹.

Q.2. Solve the differential equation x²y′′ − 7xy′ + 16y = 0 for x > 0.

Given second order Cauchy-Euler equation is:
x² y′′ − 7xy′ + 16y = 0
Let y = x^r and substitute in the given differential equation.
x² y′′ − 7xy′ + 16y = 0
x²[ xr ]′′ – 7x[ x^r ]′ + 16( xr ) = 0

x² [r(r − 1)x^r−2] – 7x [rx^r−1] + 16x^r = 0
(r² − r)xr − 7r xr + 16x^r = 0

(r² – r – 7r + 16)x^r = 0
⇒ (r – 4)² = 0
⇒ r = 4
Therefore, the solution of the given equation is y₁(x) = x⁴.
Since we got only one solution, we cannot simply write out the general solution. Let’s perform the reduction of order method.
Now, let y(x) = x⁴u(x)
Let us differentiate the above equation.
y′(x) = [x⁴u]′ = 4x³ u + x⁴ u′
Again differentiating, we get;

y′′(x) = [4x³u + x⁴u′] ′ = 12x² u + 8x³u′ + x⁴u′′
Now, take the actual equation, i.e.,
x² y′′ − 7xy′ + 16y = 0
Substitute y(x), y'(x) and y”(x) in this equation, we get;
x²[12x² u + 8x³ u′ + x⁴u′′] – 7x[4x³u + x⁴u′] + 16[x⁴u] = 0
12x⁴ u + 8x⁵ u’ + x⁶u” – 28x⁴ u – 7x⁵ u’ + 16x⁴u = 0

x⁶u” + [8x⁵ – 7x⁵]u’ + [12x⁴ – 28x⁴ + 16x⁴]u = 0
x⁶u” + x⁵ u’ = 0
Let u’ = v.
So, x⁶v’ + x⁵v = 0

x⁶(dv/dx) + x⁵v = 0

x⁶(dv/dx) = -x⁵v
(1/v) (dv/dx) = -x⁵/x⁶
(1/v) (dv/dx) = -1/x
Integrating on both sides, we get;

∫ (1/v) (dv/dx) dx = ∫(-1/x) dx

ln |v| = -ln |x| + c₀

So, v = ± e^−ln|x|+c0 = c₂/x
Now,
u(x) = ∫u′(x) dx = ∫ v(x) dx = ∫ c₂/x dx = c₂ln |x| + c₁
Hence, the general solution of the differential equation is:
y(x) = x⁴u(x) = x⁴ [c₂ ln |x| + c₁] = c₁x⁴ + c₂x⁴ ln |x|