Properties of Metals, Stress-Strain & Elastic Constants - 1 | Civil Engineering SSC JE (Technical) - Civil Engineering (CE) PDF Download
| Table of contents |

|
| Properties of Metals |

|
| Stress-Strain Curve |

|
| Simple Stress and Strain |

|
| Hooke's Law |

|
Properties of Metals
1. Ductility:
-Ductility is the property by virtue of which material can be stretched to a reduced section under the action of tensile force. Large deformations are thus possible in ductile materials before the absolute failure or rupture takes place, some of the examples are mild steel, aluminium, copper, manganese, lead, nickel, brass, bronze, monel metal etc.
2. Brittleness:
-Brittleness is the lack of ductility i.e. material can not be stretched. In brittle materials, failure takes place with a relatively smaller deformation. This property is undesirable. For brittle materials fracture point & ultimate points are same, and after proportional limit very small strain is seen. Some of the examples are cast iron, concrete and glass.
-To distinguish between these two types of materials, materials with strain less than 5% at fracture point are regarded as brittle and those having strains greater than 5% at fracture point are called ductile. (This value for mild steel at fracture is about 25%).
3. Malleability:
-The property by which a material can be uniformly extended in all direction without rupture. A malleable material possess a high degree of plasticity. This property is of great use in operations like forging, hot rolling, drop (stamping) etc.
4. Toughness:
-The property which enables materials to absorb energy without fracture. This property is very desirable in case of cyclic loading or shock loading.
-The “Modulus of toughness” is measured as area under entire stress-strain curve and is the energy absorbed by material of the specimen per unit volume upto fracture stage.
Modulus of toughness:
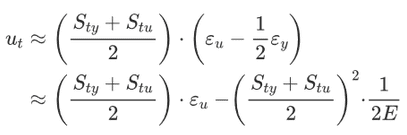
Where,
Sty is the tensile yield strength,
Stu is the tensile ultimate strength,
εy is the strain at yield,
εu is the ultimate strain (total strain at failure), and
E is the elastic modulus.
- The modules of toughness will depend upon ultimate tensile strength and strain at failure (fracture strain). Hence the material which is very ductile, will exhibit a higher modulus of toughness as the case with mild steel.
- On the other hand the “Modulus of resilience” depends upon yield strength and hence a material with higher yield strength will have higher modulus of resilience.
- The ‘Modulus of resilience’ is the maximum elastic energy per unit volume that can be absorbed without attaining plastic stage.
Modulus of resilience:
μr=
Higher toughness a desirable property in materials used for gears, chains, crane hooks, freight car etc.
Higher resilience is desirable in springs.
5. Hardness:
-Hardness is defined as the resistance to indentation or scratching or surface abrasion.
Based upon this there are two methods of hardness measurement :
(i) Scratch hardness - Commonly measured by Mohr's test.
(ii) Indentation hardness (abrasion) measured by:
- Brinell hardness method
- Rockwell hardness
- Vickers hardness
- Knoop hardness
- It should be noted that ductile materials are tough and brittle materials are hard.
6. Fatigue:
-It has been found that materials behave differently under the static loading and dynamic loading.
The behaviour of material under variable loads (dynamic loads) is referred to as “fatigue”. In recent past several failures of structures have been noted due to fatigue.
Factors affecting fatigue are :
(i) Loading conditions
(ii) Frequency of loading
(iii) Corrosion
(iv) Temperature
(v) Stress concentration
7. Creep & Stress Relaxation:
-At any temperature, a material will progressively deform with the passage of time under constant loading, even if the stress is below yield point, this phenomenon is called creep. However such deformation is negligibly small at lower temperature.
-At higher temperature, due to greater mobility of atoms, most of the materials loose their strength and elastic constants also get reduced. Hence greater deformation at elevated temperature results even under constant loading. Therefore creep is more pronounced at higher temperature, hence it must be considered for design of engines & furnaces.
-The temperature at which the creep becomes very appreciable is half of the melting point temperature on absolute scale and is known as “Homologous temperature”.
-If a wire of metal is stretched between two immovable supports, so that it has an initial tension stress so. The stress in the wire gradually diminishes, eventually reaching a constant value. This process, which is a manifestation of creep, is called “Stress relaxation”.
Stress-Strain Curve
Simple tension test for mild steel :

- A is Limit of proportionality : Beyond A linear variation ceases.
- B is Elastic limit : The maximum stress up to which a specimen regains its original length on removal of applied load. For mild steel B is very near to A. for other materials B may be greater than A.
- C' is Upper yield point : The magnitude of the stress corresponding to C' depends on the cross-sectional area, shape of the specimen and the type of the equipment used to perform the test. It has no practical significance.
- C is lower yield point : The stress at C is the yield stress (σy) with a typical value of σy = 250 N/mm2 for mild steel. The yielding begins at this stress.
- CD represents perfectly plastic region : It is the strain which occurs after the yield point C, without any increase in stress. The strain corresponding to point D is about 1.4% and corresponding to C is about 0.12% for mild steel. Hence plastic strain is 10 to 15 times of elastic strain.
- DE represents strain hardening : In this range further addition of stress gives additional strain, however strain increases with faster rate in this region. The material in this range undergoes change in its atomic and crystalline structure, resulting in increased resistance to further deformation. This portion is not used for structural design.
- E is Ultimate point : The stress corresponding to this point is ultimate stress (σy) and the corresponding strain is about 20% for mild steel.
- F is fracture point : Stress corresponding to this is called breaking stress & strain is called fracture strain.
- It is about 25% for mild steel.
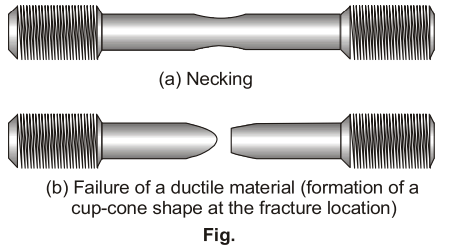
- Region between E & F is the necking region, in which area of cross-section is drastically decreased.
Important Terms:
- Elastic behavior: Stress-strain relationship is linear until the proportional limit, beyond which bending occurs until the elastic limit, where permanent deformation starts. Steel's elastic limit is hard to distinguish from the proportional limit.
- Yielding: Stress exceeding elastic limit leads to permanent deformation, yielding. Yield stress initiates plastic deformation, often with upper and lower yield points in materials like low carbon steels.
- Strain Hardening: Post-yielding, further load leads to continuous rise in stress, termed strain hardening, culminating in ultimate stress.
- Necking: Beyond ultimate stress, localized decrease in cross-sectional area leads to neck formation, causing downward curve until fracture stress.
Important Points to be noted :
1. Strain that occurs before the yield point is called elastic strain and that which occurs after yield point with no increase in stress is called plastic strain. For mild steel, Plastic Strain = 10 to 15 times of elastic strain
2. Ideal curve for tension is shown, however actual behaviour is different and indicates apparently reduced yield stress in compression for mild steel. The divergence between tension and compression results it is explained by Bauchinger and is called “Bauchinger effect”.
3. The stress is defined as the ratio of load to original area (Ao) It is also known as ‘engineering stress’ or ‘stress’ or ‘nominal stress’.
Engg. stress ‘or’ Nominal stress = 
On the contrary when changing area is taken into account, the ratio of load to actual area (A) is called ‘true stress’.
True stress = P/A
Simple Stress and Strain
-It is the internal resistance offered by the body against external loading or deformation. Stresses may be of following type :
(i) Direct stresses or normal stresses which may be tensile or compressive.
(ii) Shear or Tangential stresses.
(iii) Transverse or Bending stresses.
(iv) Torsional or Twisting stresses.
-For direct stresses, if area under consideration is original area, then it is known as engineering stress or nominal stress or simply stress. But, if the area taken is actual area, then stress is known as true stress.
Nominal Stress = 
here, Ao = Original area of specimen
A = Actual area of specimen
-When a prismatic bar is subjected to axial load, it undergoes a change in length. This change is length is usually called deformation. The deformation per unit length of the bar is termed as strain. Since strain is deformation per unit length, it is a dimensionless quantity. But sometimes in practice, strain is recorded in forms such as mm/m or µm/m etc.

Tension and Compression Monotonic Stress-strain Diagrams:

Tensile stress-strain diagram for different steels:

Stress-strain diagrams for different materials:
Hooke's Law
-It states that within elastic limit stress for most of the metals is proportional to strain.Stress ∝ Strain
Where, E = Young’s modulus of elasticity.
-Hooke’s law is valid up to limit of proportionality. However for mild steel proportional limit and Elastic limit are almost equal, but for other metals & materials elastic limit may be higher than proportional limit, for example-rubber.
-The slope of stress-strain curve is called modulus of elasticity (E). The modulus of elasticity (E) is the constant of proportionality which is defined as the intensity of stress that causes unit strain. Thus, modulus of elasticity (E) has the units same as units of stress.

Assumptions in Hooke's Law:
- Homogeneous: Properties consistent throughout.
- Isotropic: Properties uniform in all directions.
- Elastic: Reversible deformation within linear region under stress.
Proof Stress:
-When a material such as aluminium does not have an obvious yield point and yet undergoes large strains after the proportional limit is exceeded, an arbitrary yield stress may be determined by the offset method.
-A line parallel to initial linear part is drawn, which is offset by some standard amount of strain such as 0.2%. The intersection of the offset point (A) defines the yield stress of offset yield stress, which is slightly above the proportional limit and is called proof stress.

Stress-strain curve for ‘aluminium’
Solved Examples:
Question: The strain energy per unit volume of a round bar under uni-axial tension with axial stress and modulus of elasticity E is
Solution: Strain energy/volume = 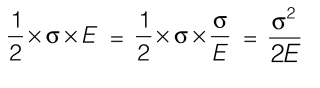
Question: A cross-section bar of area 700 mm2 is subjected to an axial load as shown in the figure below, what is the value of stress (MPa) in the section QR?
Solution:
 Axial Loading Diagram
Axial Loading Diagram
PQR = +28kN
Induced Stress, 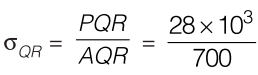 = - 40kN
= - 40kN
Question: A rod of dimension 20 mm x 20 mm is carrying an axial tensile load of 10 kN. The tensile stress developed is
Solution: Induced Stress, σ = P/A = (10 x 100)/(20 x 20) = 25 MPa
|
2 videos|122 docs|55 tests
|
FAQs on Properties of Metals, Stress-Strain & Elastic Constants - 1 - Civil Engineering SSC JE (Technical) - Civil Engineering (CE)
| 1. What are the key properties of metals? |  |
| 2. What does a stress-strain curve represent? |  |
| 3. What is the concept of simple stress and strain? |  |
| 4. What is Hooke's Law in relation to materials? |  |
| 5. How are elastic constants related to the properties of metals? |  |
|
2 videos|122 docs|55 tests
|

|
Explore Courses for Civil Engineering (CE) exam
|

|


















