Mensuration Class 6 Worksheet Maths Chapter 9
Fill in the Blanks
Q1: The length of boundary of a plane figure is called_____
Ans: Perimeter
Q2: Perimeter of rectangle = ____?
Ans: We know that the Perimeter of the rectangle =2(l+b),
Here, l=lengthb=breadth
Q3: Perimeter of square = ___?
Ans: We know that the perimeter is the length of the boundaries of a figure.
Square has four sides.
Therefore, Perimeter of square =4×side
Q4: Area of rectangle =(a)_______×(b)______squar
Ans: We know that area of rectangle =length×breadth
Therefore,
(a) Length
(b)Breadth
Q5: Area of square =(a)_______×(b)______squareunits.
Ans: We know that area of a square is side x side
Therefore,
(a) Side
(b) Side
True or False
Q6: The area of a triangle can be found using the formula Area
Ans: True
Q7: In an equilateral triangle, the perimeter is calculated by multiplying the side length by 4.
Ans: False
The perimeter of an equilateral triangle is calculated by multiplying the side length by 3.
Q8: To determine the amount of material needed to cover a square-shaped frame, Rohan needs to calculate the area of the frame.
Ans: False
To cover the border of a square-shaped frame, Rohan needs to calculate the perimeter, not the area. The perimeter will give the total length of the border material needed. The area of the frame would give the total space covered by the frame, not the length of the border material.
Crossword
Q9: Complete the crossword:
Across →
(1) Perimeter (in cm) of an equilateral triangle of side 220 cm.
(3) Perimeter (in cm) of a regular hexagon of side 84 cm.
(5) 4 m 25 cm = ________ cm.

Down ↓
(2) Perimeter (in cm) of a regular pentagon of side 120 cm.
(4) Number of unit squares (sq. cm.) enclosed in a square of side 22 cm.
(6) Distance covered along a triangular park (in 1 round) measuring 12 m, 20 m and 23 m. (distance in m)
Ans:
(1) 660
(2) 600
(3) 504
(4) 484
(5) 425
(6) 55
Answer the following Questions
Q10: Which of the following figure has a greater perimeter? Ans:
Ans:
(i) Perimeter of the square = 4 x side
= 4 x 4 cm = 16 cm
(ii) Perimeter of the rectangle
= 2 [length + breadth]
= 2[8 cm + 3 cm]
= 2 x 11 cm = 22 cm
Since 22 cm > 16 cm
∴ Rectangle has greater perimeter than the square.
Q11: Find the total distance covered by an athlete in taking 2 rounds of a rectangular park of length 150 m and breadth 80 m.
Ans:
Given the breadth of the rectangular park b= 80m and Length l= 150 m
The perimeter of the park =2 (b+l) =2×( 80 +150) = 2× 230 = 460m
Given: The athlete takes 2 rounds around the rectangular park
So, the total distance covered by the athlete = 2× 460 m = 920 m
Q12: A tailor wants to put lace around a square tablecloth of side 20 cm. He bought 1 m lace from the market. Find the length of lace left with him after completing the task.
Ans: Side = 20cm
Perimeter of Square: S X 4 = 20 X 4 = 80 cm
Length of cloth = 1m = 100 cm
Cloth left: 100 - 80 = 20cm
Q13: The length of a rectangular park is 50 m and its area is 650 m2. Find its breadth.
Ans: Length=50m
Area=650 m
So, According to the question:
Area of rectangle= Length x Breadth
650=50 x Breadth
=50 x Breadth=650
Breadth=650/50
=Breadth=13m
Q14: Find the number of square tiles required to cover the floor of a room whose length is 4 m and width 3 m, if each square tile is of side 0.2 m.
Ans: To find the number of square tiles required to cover the floor of a room, we need to first determine the area of the room in square meters. The area of a rectangle is given by the formula:
Area = Length x Width
In this case, the length of the room is 4 m and the width is 3 m, so the area of the room is 4 x 3 = 12 sq m.
Next, we need to determine the area of a single square tile. The area of a square is given by the formula:
Area = Side X 2
In this case, the side of the square tile is 0.2 m, so the area of a single tile is 0.2 X 2 = 0.04 sq m.
To find the number of tiles required to cover the floor of the room, we can divide the area of the room by the area of a single tile:
12 sq m / 0.04 sq m = 300 tiles
Therefore, the number of square tiles required to cover the floor of the room is 300 tiles.
Q15: Two equal sides of an isosceles triangle measure 10 cm each. Find the length of its third side if its perimeter is 32 cm.
Ans:
Perimeter of the triangle = sum of all the sides of it
32 = 10 + 10 + x
(let the third side be x)
32 = 20 + x
x = 32 - 20
x = 12cm
Q16: A piece of string is 60 cm long. What will be the length of each side if the string is used to form :
(a) a square
(b) an equilateral triangle
(c) a regular pentagon
Ans:
(a) Length of wire=60cm
Since,the wire is used to form a square, the length of wire becomes perimeter of the square.
Perimeter=60 cm
4 × side = 60 cm
60/4 = 15
Side =15 cm
(b) Given
length of string=60cm
If the string is used to form an equilateral triangle then the perimeter of the triangle = length of the string
Let the side of the triangle be a
a + a+ a = 60
3a =60
3a = 60
a = 20cm
(c) Given, regular pentagon(all sides equal)
perimeter= 5 × side = 60 cm
side = 12 cm.
Q17: A farmer's rectangular garden is adjacent to his house, (as shown in the figure).
The rectangular garden is 200 m long and 150 m wide. Find the cost of fencing three sides of this garden at the rate of 12 per meter.
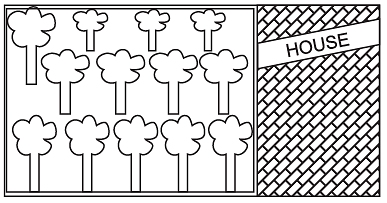
Ans:
Length of garden = 200m
Breadth of garden = 150m
Cost of fencing = 12 per meter
We have to fence only 3 sides = L+L+B
200+200+150 = 550m
Cost of Fencing = 550m = 550 x 12 = 6600 rs
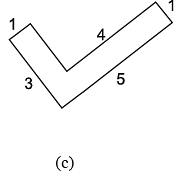
Q18: Find the perimeter of each of the following figures : (The measures are given in cm)


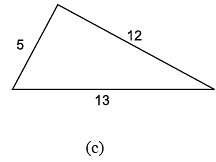
Ans:
(a) Perimeter = sum of all sides
5+ 1+ 2+ 2+ 2+1+5+1+2+2+2+1 = 26 cm
(b) Perimeter = sum of all sides
1+1+1+1+1+ 2+1+1+1+1+1+6 = 18 cm
(c) Perimeter = sum of all sides
13+5+12 = 30 cm
Q19: Find the area of each of the following figures : (The measures are given in cm)


Ans: (a) 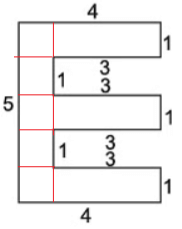
There are 3 rectangles in the picture and 5 squares
Area of one rectangle= l x b = 4X
Side of square = 1
Sides of rectangle = length = 1 and Breadth = 3
3x1= 3
No of the rectangles are 3
3x area of one rectangle = 3x3= 9
Area of square = Side2 = 1X1 = 1
No of squares 5 = 5 x 1= 5
Total Area = 9+5 = 14 sq.cm
(b)

No of squares = 8
Area of one square = 1X 1= 1
Area of all squares = 8 x 1 = 8 sq.cm
(c)

Area rectangle 1 = l x b = 3 X 1= 3
Area of Reactangle = l x b = 4 x 1 = 4
Total area = 3+4 = 7 sq. cm
Q20: Fencing the compound of a house costs ₹5452. If the rate is ₹94 per metre, find the perimeter of the compound. If the breadth is 10 m, find its length.
Ans:
Cost of fencing the compound = ₹5452
and the rate of fencing = ₹94 per metre
∴ Perimeter of the compound = 5452 ÷ 94 = 58 metres
Now breadth of the compound = 10 m.
2 [length + breadth] = 58 m
∴ length + breadth = 58 + 2 m = 29 m
∴ Length of the compound = 29 m – 10 m = 19 m.
|
92 videos|348 docs|54 tests
|
FAQs on Mensuration Class 6 Worksheet Maths Chapter 9
| 1. What is mensuration and why is it important in mathematics? |  |
| 2. How is the area of a circle calculated in mensuration? |  |
| 3. What is the difference between perimeter and area in mensuration? |  |
| 4. How is the volume of a cube calculated in mensuration? |  |
| 5. Can mensuration be used in everyday life? |  |

|
Explore Courses for Class 6 exam
|

|


















