Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-1) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 3.101
Q.1. Point A and B are 70 km. a part on a highway. A car starts from A and another car starts from B simultaneously. If they travel in the same direction, they meet in 7 hours, but if the travel towards each other, the meet in one hour. Find the speed of the two cars.
Ans. We have to find the speed of car
Let X and Y be two cars starting from points A and B respectively. Let the speed of car X be x km/hr and that of car Y be y km/hr.
Case I: When two cars move in the same directions:
Suppose two cars meet at point Q, Then,
Distance travelled by car X = AQ
Distance travelled by car Y = BQ
It is given that two cars meet in 7 hours.
Therefore, Distance travelled by car X in hours = 7x km
AQ = 7x
Distance traveled by car y in 7 hours = 7y km
BQ = 7Y
Clearly AQ - BQ = AB
7x - 7y = 70
Dividing both sides by common factor 7 we get,
x - y = 10...(i)
Case II : When two cars move in opposite direction
Suppose two cars meet at point. Then,
Distance travelled by car X = AP
Distance travelled by car Y = BP
In this case, two cars meet in 1 hour
Therefore Distance travelled by car X in1 hour = 1x km
AP = 1x
Distance travelled by car Y in 1 hour = 1y km
BP = 1y
From the above clearly,
AP + BP = AB
AP + BP = AB
x + y = 70...(ii)
By solving equation (i) and (ii), we get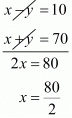
x = 40
Substituting x = 40 in equation (ii) we get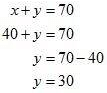
Hence, the speed of car starting from point A is 40 km / hr.
The speed of car starting from point B is 30 km / hr.
Q.2. A sailor goes 8 km downstream in 40 minutes and returns in 1 hours. Determine the speed of the sailor in still water and the speed of the current.
Ans. Let the speed of the sailor in still water be x km/hr and the speed of the current be y km/hr
Speed upstream = (x - y)km / hr
Speed downstream = (x + y)km / hr
Now, Time taken to cover 8km down stream = 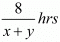
Time taken to cover 8km upstream = 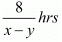
But, time taken to cover 8 km downstream in 40 minutes or 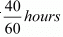 that is
that is

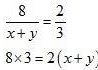
24 = 2x + 2y
Dividing both sides by common factor 2 we get
12 = x + y...(i)
Time taken to cover 8km upstream in 1hour
8 = x - y...(ii)
By solving these equation (i) and (ii) we get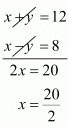
x = 10
Substitute x = 10 in equation (i) we get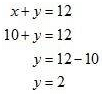
Hence, the speed of sailor is 10 km / hr
The speed of current is 2 km / hr
Q.3. The boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of stream and that of the boat in still water.
Ans. Let the speed of the boat in still water be x km/hr and the speed of the stream be y km/hr
Speed upstream = (x - y) km / hr
Speed down stream = (x + y) km / hr
Now,
Time taken to cover 30 km upstream =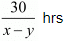
Time taken to cover 44 km down stream =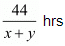
But total time of journey is 10 hours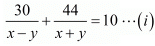
Time taken to cover 40 km upstream =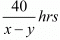
Time taken to cover 55 km down stream =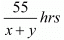
In this case total time of journey is given to be 13 hours
Therefore,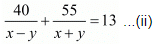
Putting and
and 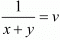 in equation (i) and (ii) we get
in equation (i) and (ii) we get
30u + 44v = 10
40u + 55v = 10
30u + 44v - 10 = 0...(iii)
40u + 55v - 13 = 0...(iv)
Solving these equations by cross multiplication we get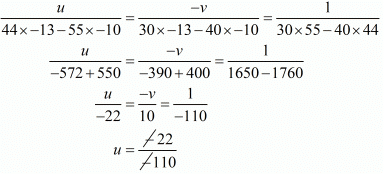
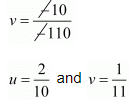
Now,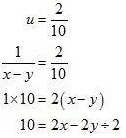

By solving equation (v) and (vi) we get ,
Substituting x = 8 in equation (vi) we get ,
Hence, speed of the boat in still water is 8 km/ hr
Speed of the stream is 3 km /hr
Page No 3.102
Q.4. A boat goes 24 km upstream and 28 km downstream in 6 hrs. It goes 30 km upstream and 21 km downstream in 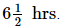 Find the speed of the boat in still water and also speed of the stream.
Find the speed of the boat in still water and also speed of the stream.
Ans. We have to find the speed of the boat in still water and speed of the stream
Let the speed of the boat in still water be x km/hr and the speed of the stream be y km/hr then
Speed upstream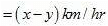
Sped down stream 
Now, Time taken to cover 28 km down stream =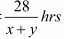
Time taken to cover 24 km upstream = 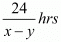
But, total time of journey is 6 hours
Time taken to cover 30 km upstream =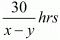
Time taken to cover 21 km down stream = 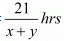
In this case total time of journey is given to 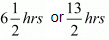
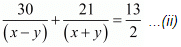
By 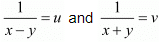 in equation (i) and (ii) we get
in equation (i) and (ii) we get
24u + 28v = 6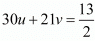
24u + 28v - 6 = 0...(iii)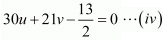
Solving these equations by cross multiplication we get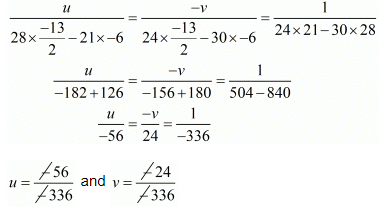
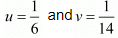
Now,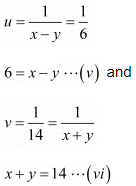
By solving equation (v) and (vi) we get,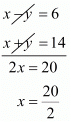
x = 10
By substituting x = 10 in equation (vi) we get
Hence, the speed of the stream is 4km / hr
The speed of boat is 10 km / hr.
Q.5. A man walks a certain distance with certain speed. If he walks 1/2 km an hour faster, he takes 1 hour less. But, if he walks 1 km an hour slower, he takes 3 more hours. Find the distance covered by the man and his original rate of walking.
Ans. Let the actual speed of the train be x Km/hr and the actual time taken by y hours. Then,
Distance covered = speed x distance
= x x y
= xy...(i)
If the speed is increased by 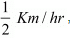 then time of journey is reduced by 1 hour i.e., when speed is
then time of journey is reduced by 1 hour i.e., when speed is  time of journey is(y - 1)hours
time of journey is(y - 1)hours
∴ Distance covered = xy km
- 2x + y - 1 = 0...(ii)
When the speed is reduced by 1km / hr, then the time of journey is increased by 3 hours i.e., when speed is (x - 1) km/ hr, time of journey is (y + 3)hours
∴ Distance covered = xy
xy = (x - 1)(y + 3)
xy = (x - 1)(y + 3)
xy = xy - 1y + 3x - 3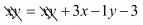
3x - 1y - 3 = 0...(iii)
Thus we obtain the following equations
- 2x + 1y - 1 = 0
3x - 1y - 3 = 0
By using elimination method, we have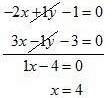
Putting the value x = 4 in equation (iii) we get
3x - 1y - 3 = 0
3 x 4 - 1y - 3 = 0
12 - 1y - 3 = 0
12 - 3 - 1y = 0
9 - 1y = 0
-1y = -9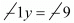
y = 9
Putting the value of x and y in equations (i) we get
Distance covered = xy
= 4 x 9
= 36km
Hence, the distance is 36 km,
The speed of walking is 4 km / hr.
Q.6. A person rowing at the rate of 5 km/h in still water , takes thrice as much time in going 40 km upstream as in going 40 km downstream . Find the speed of the stream.
Ans. Speed of the boat in still water = 5 km/h
Let the speed of stream = x km/h
∴ Speed of boat upstream = (5 − x) km/h
Speed of boat downstream = (5 + x) km/h
Time taken to row 40 km upstream = 
Time taken to row 40 km downstream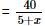
According to the given condition,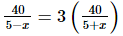

Therefore, the speed of the stream is 2.5 km/h.
Q.7. Ramesh travels 760 km to his home partly by train and partly by car. He takes 8 hours if he travels 160 km. by train and the rest by car. He takes 12 minutes more if the travels 240 km by train and the rest by car. Find the speed of the train and car respectively.
Ans. Let the speed of the train be x km/hour that of the car be y km/hr, we have the following cases
Case I: When Ramesh travels 760 Km by train and the rest by car
Time taken by Ramesh to travel 160 Km by train =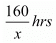
Time taken by Ramesh to travel (760-160) =600 Km by car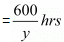
Total time taken by Ramesh to cover 760Km =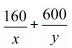
It is given that total time taken in 8 hours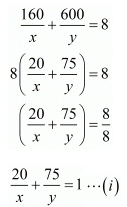
Case II: When Ramesh travels 240Km by train and the rest by car
Time taken by Ramesh to travel 240 Km by train =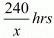
Time taken by Ramesh to travel (760-240) =520Km by car =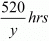
In this case total time of the journey is 8 hours 12 minutes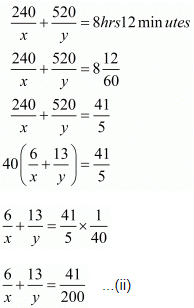
Putting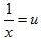 and,
and,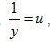 the equations (i) and (ii) reduces to
the equations (i) and (ii) reduces to
20u + 75v = 1...(iii)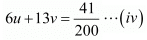
Multiplying equation (iii) by 6 and (iv) by 20 the above system of equation become
120u + 450v = 6...(v)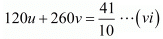
Subtracting equation (vi) from (v) we get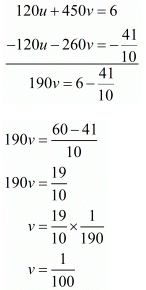
Putting 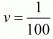 in equation (v), we get
in equation (v), we get

Now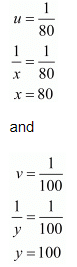
Hence, the speed of the train is 80 km / hr,
The speed of the car is 100 km/ hr.
Q.8. A man travels 600 km partly by train and partly by car. If the covers 400 km by train and the rest by car, it takes him 6 hours 30 minutes. But, if the travels 200 km by train and the rest by car, he takes half an hour longer. Find the speed of the train and that of the car.
Ans. Let the speed of the train be x km/hr that of the car be y km/hr, we have the following cases:
Case I: When a man travels 600Km by train and the rest by car
Time taken by a man to travel 400 Km by train =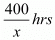
Time taken by a man to travel (600-400) =200Km by car =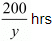
Total time taken by a man to cover 600Km = 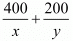
It is given that total time taken in 8 hours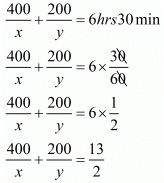
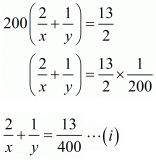
Case II: When a man travels 200Km by train and the rest by car
Time taken by a man to travel 200 Km by train =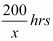
Time taken by a man to travel (600-200) = 400 Km by car 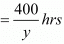
In this case, total time of the journey in 6 hours 30 minutes + 30 minutes that is 7 hours,
Putting 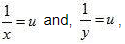 the equations (i) and (ii) reduces to
the equations (i) and (ii) reduces to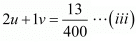
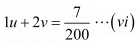
Multiplying equation (iii) by 6 the above system of equation becomes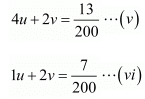
Substituting equation (vi) and (v), we get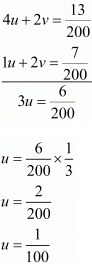
Putting 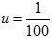 in equation (vi), we get
in equation (vi), we get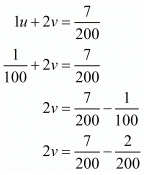
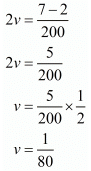
Now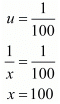
and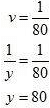
Hence, the speed of the train is 100 km/ hr,
The speed of the car is 80 km / hr.
Q.9. Places A and B are 80 km apart from each other on a highway. A car starts from A and other from B at the same time. If they move in the same direction, they meet in 8 hours and if they move in opposite directions, they meet in 1 hour and 20 minutes. Find the speeds of the cars.
Ans. Let x and y be two cars starting from points A and B respectively.
Let the speed of the car X be x km/hr and that of the car Y be y km/hr.
Case I: When two cars move in the same directions:
Suppose two cars meet at point Q, then,
Distance travelled by car X = AQ
Distance travelled by car Y = BQ
It is given that two cars meet in 8 hours.
Distance travelled by car X in 8 hours = 8x km
AQ = 8x
Distance travelled by car Y in 8 hours = 8y km
BQ = 8y
Clearly AQ-BQ = AB
8x - 8y = 80
Both sides divided by 8, we get
x - y = 10...(i)
Case II: When two cars move in opposite direction
Suppose two cars meet at point P, then,
Distance travelled by X car X=AP
Distance travelled by Y car Y=BP
In this case, two cars meet in 1 hour 20 minutes, we can write it as 1 hour 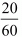 or
or 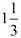 hours that is 4/3 hours.
hours that is 4/3 hours.
Therefore,
Distance travelled by car y in 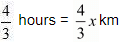
Distance travelled by car y in 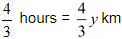
AP + BP = AB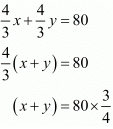
x + y = 60...(ii)
By solving (i) and (ii) we get,
By substituting x = 35 in equation (ii), we get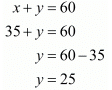
Hence, speed of car X is 35 km/ hr, speed of car Y is 25 km/hr.
Q.10. A boat goes 12 km upstream and 40 km downstream in 8 hours. I can go 16 km upstream and 32 km downstream in the same time. Find the speed of the boat in still water and the speed of the stream.
Ans. We have to find the speed of the boat in still water and speed of the stream
Let the speed of the boat in still water be km/hr and the speed of the stream be km/hr then
Speed upstream = (x - y)km / hr
Speed down stream = (x + y)km / hr
Now, Time taken to cover km upstream = 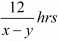
Time taken to cover km down stream = 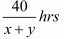
But, total time of journey is 8 hours
Time taken to cover km upstream =
Time taken to cover km down stream =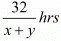
In this case total time of journey is given to 8 hrs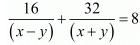 ...(ii)
...(ii)
By 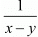 and in equation (i) and (ii) we get
and in equation (i) and (ii) we get
12u + 40v = 8
16u + 32v = 8
12u + 40v - 8 = 0...(iii)
16u + 32v - 8 = 0...(iv)
Solving these equations by cross multiplication we get
Now,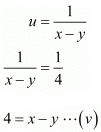
and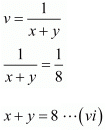
By solving equation (v) and (vi) we get,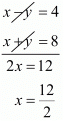
x = 6
By substituting x = 6 in equation (vi) we get
x + y = 8
6 + y = 8
y = 8 - 6
y = 2
Hence, the speed of boat in still water is 6 km/hr,
The speed of the stream is 2 km/hr.
FAQs on Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-1) - RD Sharma Solutions for Class 10 Mathematics
| 1. What is the meaning of a pair of linear equations in two variables? |  |
| 2. How can we solve a pair of linear equations in two variables graphically? |  |
| 3. What is the significance of the slope-intercept form in solving pair of linear equations in two variables? |  |
| 4. How can we determine if a pair of linear equations in two variables has a unique solution, no solution, or infinite solutions? |  |
| 5. What are some real-life applications of pair of linear equations in two variables? |  |

|
Explore Courses for Class 10 exam
|

|

















