Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-6) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 3.116
Q.4. If a pair of linear equations is consistent, then the lines representing them are either _______ or ________.
Ans. If a pair of linear equations is consistent, then two case arises:
Case 1: When the lines are coincident, they have infinitely many solutions.
Case 2: When the lines are intersecting, they have a unique solution.
Hence, If a pair of linear equations is consistent, then the lines representing them are either coincident or intersecting.
Q.5. There is (are) ________ value(s) of c for which the pair of equations cx – y = 2 and 6x – 2y = 3 have infinitely many solutions.
Ans. If the system of equations a1x+b1y+c1=0 and a2x+b2y+c2=0 has infinitely many solutions, then 
Since, the system of equations cx – y = 2 and 6x – 2y = 3 has infinitely many solutions
Therefore,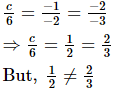
Therefore, for no value of c the pair of equations cx – y = 2 and 6x – 2y = 3 have infinitely many solutions.
Hence, there is (are) no value(s) of c for which the pair of equations cx – y = 2 and 6x – 2y = 3 have infinitely many solutions.
Q.6. If one equation of a pair of dependent linear equations is 5x – 7y + 2 = 0, then the second equation is given by _______.
Ans. To get the dependent linear equation, multiply the given equation by any non-zero integer.
If we multiply the given equation by any non-zero integer a, we get
5ax – 7ay + 2a = 0
Hence, the second equation is given by 5ax – 7ay + 2a = 0, where a is any non-zero integer.
Q.7. If a pair of linear equations is consistent with a unique solution, then the lines representing them are _______.
Ans. If a pair of linear equations is consistent, then two case arises:
Case 1: When the lines are coincident, they have infinitely many solutions.
Case 2: When the lines are intersecting, they have a unique solution.
Hence, if a pair of linear equations is consistent with a unique solution, then the lines representing them are intersecting.
Q.8. The pair of equations λx + 3y = 7, 2x + 6y = 14 will have infinitely many solutions for λ = ________.
Ans. If the system of equations a1x+b1y+c1=0 and a2x+b2y+c2=0 has infinitely many solutions, then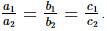
Since, the system of equations λx + 3y = 7, 2x + 6y = 14 has infinitely many solutions
Therefore,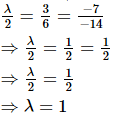
Hence, the pair of equations λx + 3y = 7, 2x + 6y = 14 will have infinitely many solutions for λ = 1.
Q.9. If the pair of equations 2x + 3y – 5 = 0 and px – 6y – 8 = 0 has a unique solution for all real values of p except _______.
Ans. If the system of equations a1x+b1y+c1=0 and a2x+b2y+c2=0 has a unique solution, then 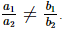
Since, the system of equations 2x + 3y – 5 = 0 and px – 6y – 8 = 0 has a unique solution
Therefore,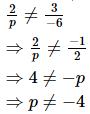
Hence, if the pair of equations 2x + 3y – 5 = 0 and px – 6y – 8 = 0 has a unique solution for all real values of p except –4.
Q.10. If the lines represented by the equations 3x – y – 5 = 0 and 6x – 2y – p = 0 are parallel, then p is equal to ________.
Ans. If the system of equations a1x+b1y+c1=0 and a2x+b2y+c2=0 has no solution, i.e., they are parallel, then
Since, the system of equations 3x – y – 5 = 0 and 6x – 2y – p = 0 are parallel
Therefore,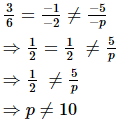
Hence, if the lines represented by the equations 3x – y – 5 = 0 and 6x – 2y – p = 0 are parallel, then p is equal to all real values except 10.
Q.11. If x = a, y = b is the solution of the pair of equations x – y = 2 and x + y = 4, then a = _______ and b = _______.
Ans. Since, x = a, y = b is the solution of the pair of equations x – y = 2 and x + y = 4
Therefore, x = a, y = b satisfies the equations x – y = 2 and x + y = 4.
a − b = 2 ...(1)
a + b = 4 ...(2)
Solving (1) and (2), we get
a = 3 and b = 1
Hence, a = 3 and b = 1.
Q.12. If the pair of equations ax + 2y = 7 and 3x + by = 16 represent parallel lines, then ab = ________.
Ans. If the system of equations a1x+b1y+c1=0 and a2x+b2y+c2=0 has no solution, i.e., they are parallel, then 
Since, the system of equations ax + 2y = 7 and 3x + by = 16 represent parallel lines
Therefore,
Hence, If the pair of equations ax + 2y = 7 and 3x + by = 16 represent parallel lines, then ab = 6.
Q.13. The line 4x + 3y – 12 = 0 cuts the coordinate axes at A and B. The area of ΔOAB is _________.
Ans. The given equation is 4x + 3y – 12 = 0 ...(i)
Solving equation (i), we get
4x + 3y − 12 = 0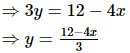
When x = 0, y = 4
When x = 3, y = 0
On plotting these points on a graph, we get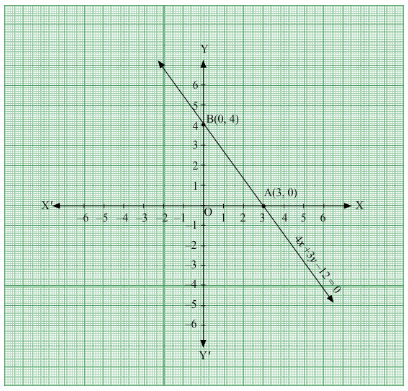
We can see that OA = 3 units and OB = 4 units
Area of ΔOAB = 1/2 × OA × OB
= 1/2×3×4
= 6
Hence, the area of ΔOAB is 6 square units.
Q.14. If 2x+y = 2x–y = √8, then x = ________ and y = ________.
Ans. Given: 2x + y = 2x – y = √8
Now, 2x + y = √8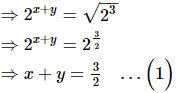
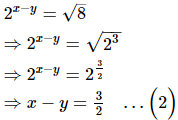
Solving (1) and (2), we get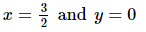
Hence, x = 
Q.15. The system of equations ax + 3y = 1, –12x + ay = 2 has ________ for all real values of a.
Ans. The given system of equations are:
ax + 3y = 1 ...(i)
–12x + ay = 2 ...(ii)
Now,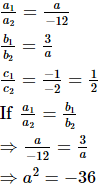
Which is not possible for any value of a.
Thus,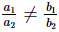 for all real values of a.
for all real values of a.
Hence, the system of equations ax + 3y = 1, –12x + ay = 2 has a unique solution for all real values of a.
Page No 3.117
Q.1. Write the value of k for which the system of equations x + y − 4 = 0 and 2x + ky − 3 = 0 has no solution.
Ans. The given system of equations is
x + y - 4 = 0
2x + ky - 3 = 0
a1 = 1, a2 = 2, b1 = 1, b2 = k, c1 = 4, c2 = 3
For the equations to have no solutions
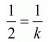
By cross multiplication we get,
1 x k = 1 x 2
k = 2
Hence, the value of k is 2 when system equations has no solution.
Q.2. Write the value of k for which the system of equations has infinitely many solutions.
2x − y = 5
6x + ky = 15
Ans. The given systems of equations are
2x - y = 5
6x + ky = 5
a1 = 2, a2 = 6, b1 = 1, b2 = k, c1 = 5, c2 = 15
For the equations to have infinite number of solutions, 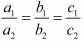
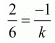
By cross Multiplication we get,
2k = -6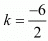
k = -3
Hence the value of k is - 3 when equations has infinitely many solutions.
Q.3. Write the value of k for which the system of equations 3x − 2y = 0 and kx + 5y = 0 has infinitely may solutions.
Ans. The given equations are
3x - 2y = 0
kx + 5y = 0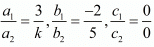
For the equations to have infinite number of solutions,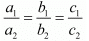
Therefore,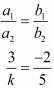
By cross multiplication we have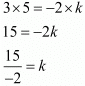
Hence, the value of k for the system of equation 3x - 2y = 0 and kx + 5y = 0 is .
.
Q.4. Write the value of k for which the system of equations x + ky = 0, 2x − y = 0 has unique solution.
Ans. The given equations are
x + ky = 0
2x − y = 0
a1 = 1, a2 = 2,b1 = k,b2 = −1
For unique solution
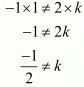
For all real values of k, except 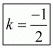 the equations have unique solutions.
the equations have unique solutions.
Q.5. Write the set of values of a and b for which the following system of equations has infinitely many solutions.
2x + 3y = 7
2ax + (a + b)y = 28
Ans. The given equations are
2x + 3y - 7 = 0
2ax + (a + b)y - 28 = 0
For the equations to have infinite number of solutions,
Therefore
Let us take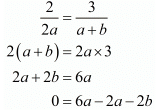
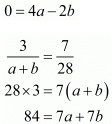
By dividing both the sides by 7 we get,
12 = a + b ...(ii)
By multiplying equations (ii) by 2 we get
24 = 2a + 2b ...(iii)
Substituting (iii) from (i) we get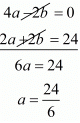
a = 4
Subtracting a = 4 in equation ...(iii) we have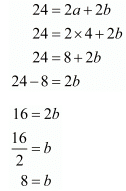
Hence, the value of a = 4, b = 8 when system of equations has infinity many solutions.
Q.6. For what value of k, the following pair of linear equation has infinitely many solutions?
10x + 5y − (k − 5) = 0
20x + 10y −k = 0
Ans. The given equations are
10x + 5y - (k − 5) = 0
20x + 10y - k = 0
For the equations to have infinite number of solutions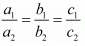
Let us take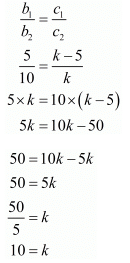
Hence, the value of k = 10 when the pair of linear equations has infinitely many solutions.
Q.7. Write the number of solution of the following pair of linear equations:
x + 2y − 8 = 0
2x + 4y = 16
Ans. The given equations are
x + 2y - 8 = 0
2x + 4y - 16 = 0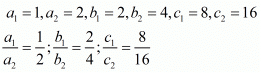

Every solution of the second equation is also a solution of the first equation.
Hence, there are infinite - Solution,the system equation is consistent.
Q.8. Write the number of solutions of the following pair of linear equations:
x + 3y − 4 = 0
2x + 6y = 7
Ans. The given linear pair of equations are
x + 3y - 4 = 0
2x + 6y = 7
a1 = 1, a2 = 2, b1 = 3, b2 = 6, c1 = 4, c2 = 7
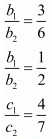
If  then
then
a1b2 = a2b1
a1b2 - a2b1 = 0
1 x 6 - 2 x 3 = 0
6 - 6 = 0
Hence, the number of solutions of the pair of linear equation is 0
Therefore, the equations have no solution.
Page No 3.12
Q.1. Akhila went to a fair in her village. She wanted to enjoy rides in the Giant Wheel and play Hoopla (a game in which you throw a rig on the items kept in the stall, and if the ring covers any object completely you get it.) The number of times she played Hoopla is half the number of rides she had on the Giant Wheel. Each ride costs Rs 3, and a game of Hoopla costs Rs 4. If she spent Rs 20 in the fair, represent this situation algebraically and graphically.
Ans. Let no. of ride is x and no. of Hoopla is y. He paid Rs 20 for x ride and y for Hoopla.
The cost of ride is Rs 3 and cost of Hoopla is Rs 4. then 3x + 4y = 20
The number of Hoopla is the half number of ride, then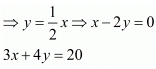
Hence algebraic equations are 3x + 4y = 20 and x - 2y = 0
Now, we draw the graph for algebraic equations.
Q.2. Aftab tells his daughter, "Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be". Is not this interesting? Represent this situation algebraically and graphically.
Ans. Let age of Aftab is x years and age of his daughter is y years. Years ago his age wastimes older as her daughter was. Then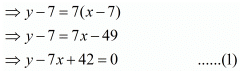
Three years from now, he will be three times older as his daughter will be, then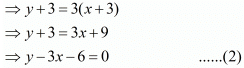
Hence the algebraic representation are y - 3x - 6 = 0 and y - 7x + 42 = 0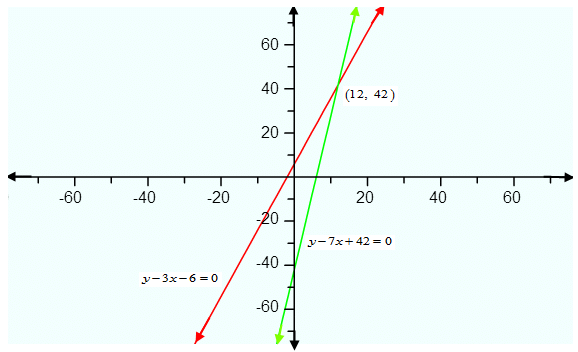
Q.3. The path of a train A is given by the equation 3x + 4y − 12 = 0 and the path of another train B is given by the equation 6x + 8y − 48 = 0. Represent this situation graphically.
Ans. The given equation are 3x + 4y - 12 = 0 and 6x + 8y - 48 = 0
In order to represent the above pair of linear equation graphically, we need
Two points on the line representing each equation. That is, we find two solutions
of each equation as given below:
We have,
3x + 4y - 12 = 0
Putting y = 0, we get
3x + 0 - 12 = 0
⇒ x = 4
Putting x = 0 we get
0 + 4y - 12 = 0
⇒ y = 3
Thus, two solution of equation 3x + 4y - 12 = 0 are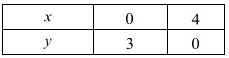
We have 6x + 8y - 48 = 0
Putting y = 0, we get
6x + 0 - 48 = 0
⇒ x = 8
Putting x = 0 we get
0 + 8y - 48 = 0
⇒ y = 6
Thus, two solution of equation 6x + 8y - 48 = 0 are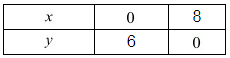
Now we plot the point A(4,0) and B(0,3) and draw a line passing through
These two points to get the graph o the line represented by equation (1)
We also plot the points C(8,0) and D(0,6) and draw a line passing through
These two points to get the graph O the line represented by equation (2)
We observe that the line parallel and they do not intersect anywhere.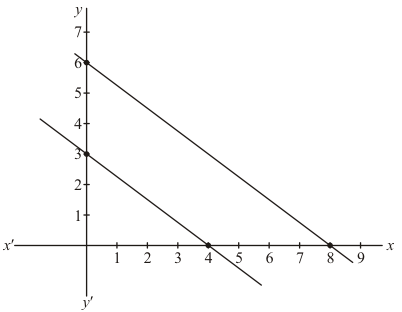
FAQs on Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-6) - RD Sharma Solutions for Class 10 Mathematics
| 1. How do you determine the number of solutions for a pair of linear equations in two variables? |  |
| 2. Can a pair of linear equations in two variables have more than one solution? |  |
| 3. How are the graphical solutions of a pair of linear equations helpful in understanding the concept of simultaneous equations? |  |
| 4. Is it possible for a pair of linear equations in two variables to have no solution? |  |
| 5. How can the elimination method be used to solve a pair of linear equations in two variables? |  |

|
Explore Courses for Class 10 exam
|

|

















