Courses
Get the App Signup / Login

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

Mechanical Engineering SSC JE (Technical)

Mechanical Engineering : Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

The document Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev is a part of the Mechanical Engineering Course Mechanical Engineering SSC JE (Technical).
All you need of Mechanical Engineering at this link: Mechanical Engineering


THIN & THICK CYLINDERS AND SPHERES

THIN CYLINDERS

  •  If the thickness of the cylinder is less than 1/10 to 1/15 of the diameter of the cylinder,  it is treated as the thin cylinder.
  •  It is assumed that the stresses are uniformly distributed through out the thickness ofthe wall.
  •  'Hoop stress’ or ‘Circumferential stress’ is given by

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

  •   ‘Longitudinal stress’ is given by

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

  •  The Maximum shear stress is given by

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

  •  Hoop strain is given by

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

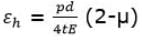
  •  Longitudinal strain is given by

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

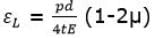
  •  Volumetric strain is given by

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

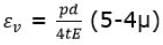
Where
p = internal pressure
d = diameter of cylinder
t = thickness of the cylinder
μ = Poisson's ratio

  •  If ‘sa’ be the permissible tensile stress for the shell material, then from strength  point of view, the major principal stress (s) should be less than or equal to sa

Hence

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev
or
Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

THIN SPHERICAL SHELLS 

  •  In case of thin spherical shells, longitudinal stress and circumferential stress are equal and are given by

s1 =s2 = Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev (tensile in nature)

  •  The maximum shear stress,  

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

  •  The strain in any direction is given by

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

  •   The volumetric strain is given by

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRevCYLINDERS WITH HEMISPHERICAL ENDS

Let tc = thickness of the cylinder
ts = thickness of the hemisphere

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

  •   Hoop stress in cylindrical part

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

  •   Hoop stress in hemispherical part

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

  •  Longitudinal stress in cylindrical part

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

  •  Longitudinal stress in hemispherical part

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

  •   Circumferential strain in hemispherical part

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

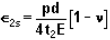
  •   Circumferential strain in cylindrical part

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

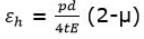
  •   For the condition of no distortion of the junction  

Thus, equating the two strains in order that there shall be no distortion of the junction.

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

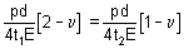
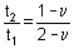
This means thickness of cylindrical part should be more than the hemispherical part.

  •  For the condition of same maximum stress in cylindrical and hemispherical parts,

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev
THICK CYLINDRICAL SHELL

  •   If the thickness of shell is greater than of
    Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

 its diameter then it is called thick shell.

  •   In thick cylinders the circumferential stress no longer remains constant, but varies  along the thickness and the radial pressure (px) is also not negligible.

The following three types of stresses are existing in thick cylinders :

(i) The radial pressure ‘px’ (compressive)
(ii) The hoop stress fx (tensile)
(iii) The longitudinal tensile stress po (tensile)

  •  The longitudinal stress may be given by

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev

Hoop stress, is given by
Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev
Radial pressure is given by
Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev
Equation (ii) and (iii) are called Lame’s equation.
ro = outer radius of shell
ri = inner radius of shell
A and B are Lame’s constant

Note:-

1. Longitudinal tension is uniform across the thickness.
2. Hoop tension vary form maximum at inner face to minimum at outer face hyperbolically.
3. Radial compression varies from maximum at inner face to zero at outer face (atm.) hyperbolically.

Offer running on EduRev: Apply code STAYHOME200 to get INR 200 off on our premium plan EduRev Infinity!
Download EduRev app here for Mechanical Engineering preparation.

Up next

Author
Pioneer Academy
Views
3.2K
Rating
4.8
Description
Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev notes for Mechanical Engineering is made by best teachers who have written some of the best books of Mechanical Engineering. It has gotten 3202 views and also has 4.8 rating. You can download Free Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev pdf from EduRev by using search above. You can also find Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev ppt and other Mechanical Engineering slides as well. If you want Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev Tests & Videos, you can search for the same too. Mechanical Engineering Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev Summary and Exercise are very important for perfect preparation. You can see some Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev sample questions with examples at the bottom of this page. Complete Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev chapter (including extra questions, long questions, short questions, mcq) can be found on EduRev, you can check out Mechanical Engineering lecture & lessons summary in the same course for Mechanical Engineering Syllabus. EduRev is like a wikipedia just for education and the Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev images and diagram are even better than Byjus! Do check out the sample questions of Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev for Mechanical Engineering, the answers and examples explain the meaning of chapter in the best manner. This is your solution of Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev search giving you solved answers for the same. To Study Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material, Mechanical Engineering Mechanical Engineering Notes | EduRev for Mechanical Engineering this is your one stop solution.

Related Searches

past year papers

,

Sample Paper

,

Extra Questions

,

Mechanical Engineering Mechanical Engineering Notes | EduRev

,

Free

,

shortcuts and tricks

,

study material

,

MCQs

,

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material

,

pdf

,

Mechanical Engineering Mechanical Engineering Notes | EduRev

,

Semester Notes

,

Important questions

,

Objective type Questions

,

mock tests for examination

,

Mechanical Engineering Mechanical Engineering Notes | EduRev

,

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material

,

Exam

,

Chapter 3 Thin and Thick Cylinders and Spheres - Strength of Material

,

ppt

,

Viva Questions

,

Previous Year Questions with Solutions

,

Summary

,

practice quizzes

,

video lectures

;
Follow Us
© EduRev