First Law Applied to Flow Processes | Mechanical Engineering SSC JE (Technical) PDF Download
FIRST LAW APPLIED TO FLOW PROCESSES
Steady Flow Process
In a flow if fluid properties do not change with time at any given location, the process is steady flow process.
- In steady flow process there is no accumulation of mass or energy in control volume i.e. conservation of mass and energy occurs.

A1, A2 — cross-section of stream, (m2)
m1, m2 — mass flow rate, (kg/s)
p1, p2 — pressure, (absolute), (N/m2)
v1, v2 — specific volume, (m3/kg)
u1, u2 — specific internal energy, (J/kg)
V1, V2 — velocity, (m/s)
Z1, Z2 — elevation above an arbitrary datum, (m)
dQ/dt— net rate of heat transfer through the control surface, (J/s)
dWx/dt—net rate of work transfer through the control surface, (J/s)
t – time(s)
Now,
By conservation of mass
m1 = m2

m1, m2 — mass flow rate entering and leaving the control volume.
- Conservation of Energy (Steady flow energy equation SFEE)
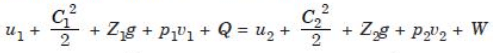
u= internal energy per kg of fluid
C= velocity of fluid
- Per unit mass basis

a)For one fluid stream SFEE (per unit time) is used.
b)For more than one fluid stream SFEE (per unit mass) is used.
c)Application of SFEE is steady flow processes
Nozzless & Diffusers


where, h is in kJ/ kg
- A nozzle is a device which increases the velocity or K.E. of fluid at the expense of its pressure drop.
- A diffuser is a device which increases the pressure of fluid at the expense of K.E.
Throttling Device
Throttling device is the generic name of any device or process that simply dissipates pressure energy m˙pv by irreversibly converting it into thermal energy. Unlike nozzles and diffusers, throttling devices provide no form of useful energy recovery.


z1 = z2, V1, V2 are negligible
h1 = h2
- When a fluid flow through a narrow passage like an orifice, partially opened valve, there is an appreciable drop in pressure. The process is throttling process.
- Throttling is an isenthalpic process.
Turbine and Compressor
Turbine is the device in which fluid expands. During the expansion work will be done by the fluid to drive, for example, electric generation. In this case, power output occurs.
Compressor is the device which is used to compress the fluid and increase its pressure. That means power input is required.
- The 1st law of thermodynamics:
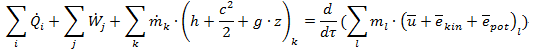
The change of kinetic energy and potential energy of fluid flowing into and out of turbines and compressors are very small that can usually be neglected:
(ekin)out – (ekin)in≈0 → c2out – c2in≈0
(epot)out – (epot)in≈0 → g•(zout – zin)≈0
Turbine and compressors are also regarded as steady-flow engineering device, so the term at the right-hand side equals zero:
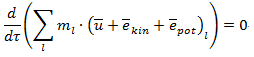
Furthermore, mout=min because of conservation of mass.
So now we obtain a simplified expression for turbine and compressor:
q+w+ hin – hout=0
where:
- q=heat transferred per unit mass
- w=work done by turbine or on compressor per unit mass
- hin= specific enthalpy of inlet fluid
- hout= specific enthalpy of outlet fluid
As discussed above,
- w<0 → turbine
 = (h1 - h2) for turbine
= (h1 - h2) for turbine
- w>0 → compressor
 = (h2 - h1) for compressor
= (h2 - h1) for compressor
Heat Exchanger
- A heat exchanger is a system used to transfer heat between two or more fluids. Heat exchangers are used in both cooling and heating processes. The fluids may be separated by a solid wall to prevent mixing or they may be in direct contact.

 z1 = z2, V1, V2 are negligible
z1 = z2, V1, V2 are negligible
|
5 videos|103 docs|59 tests
|
FAQs on First Law Applied to Flow Processes - Mechanical Engineering SSC JE (Technical)
| 1. What is the First Law of Thermodynamics and how is it applied to flow processes in Mechanical Engineering? |  |
| 2. How is the First Law applied to flow processes in Mechanical Engineering? |  |
| 3. Can you provide an example of how the First Law is used to analyze a flow process in Mechanical Engineering? |  |
| 4. How does the First Law help in improving the energy efficiency of flow processes in Mechanical Engineering? |  |
| 5. Are there any limitations or constraints in applying the First Law to flow processes in Mechanical Engineering? |  |
|
5 videos|103 docs|59 tests
|

|
Explore Courses for Mechanical Engineering exam
|

|


















