Entropy | Mechanical Engineering SSC JE (Technical) PDF Download
ENTROPY
- Two reversible adiabatic paths cannot intersect each other which violates the Kelvin - Plank's statement.
- Clausius Theorem
Any reversible path may be substituted by a reversible zigzag path between the same end states, consisting of a reversible adiabatic followed by a reversible isotherm and then by a reversible adiabatic such that the heat transferred during the isothermal process is the same as that transferred during the original process.
- The cyclic integral of (dQ/T) for a reversible cycle is equal to zero.

- Entropy:
The entropy of a system is a thermodynamic property which is a measure of the degree of molecular disorder existing in the system. It describes the randomness or uncertainty of the system, It is a function of a quantity of heat which shows the possibility of conversion of heat into work. Thus, for maximum entropy, there is minimum availability for conversion into work and minimum entropy there is a maximum availability for conversion into work.
Characteristics:
- It increases when heat is supplied irrespective of the fact whether the temperature changes or not.
- It decreases when heat is removed whether the temperature changes or not.
- It remains unchanged in all adiabatic reversible processes.
- The increase in entropy is small when heat is added at a high temperature and is greater when heat addition is made at a lower temperature.

- For a reversible adiabatic process
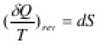
=> dS = 0 (∵ dQ = 0)
∴ S = constant
Thus a reversible adiabatic process is an isentropic process.
- For a reversible isothermal process
At a temperature, To
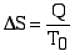
CLAUSIS' INEQUALITY
The Clausius theorem (1855) states that a system (heat engine or heat pump) exchanging heat with external reservoirs and undergoing a cyclic process, is one that ultimately returns a system to its original state,
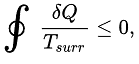
where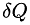 is the infinitesimal amount of heat absorbed by the system from the reservoir and
is the infinitesimal amount of heat absorbed by the system from the reservoir and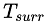 is the temperature of the external reservoir (surroundings) at a particular instant in time.
is the temperature of the external reservoir (surroundings) at a particular instant in time.
Remember:-
The equality sign holds good for a reversible process and the inequality sign for an irreversible process.
• Entropy principle:
For an isolated reversible system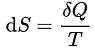
For an isolated irreversible system
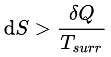
The total entropy of an isolated system can never decrease over time and is constant if and only if all processes are reversible. Isolated systems spontaneously evolve towards thermodynamic equilibrium, the state with maximum entropy.
• It is also a statement of the second law of thermodynamics.
• Entropy increase of the isolated system is a measure of the extent of the irreversibility
of the process undergone by the system.
• When the system is at equilibrium, any conceivable change in entropy would be
zero.
Application of entropy principle
• Transfer of heat through a finite Temperature difference.

Mixing of two fluids

Final temp (tf) =
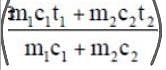

Maximum work is obtainable from two finite identical bodies at T1 and T2.

Final temperature of the two bodies (Tf) =


- The final temperature of two bodies initially at T1 & T2, can range from (T1 + T2)/2 with no delivery of work to
 with maximum delivery of work.
with maximum delivery of work.
- Maximum work obtained with finite body & TER


T = temp. of body
To = temp. of TER
- Adiabatic dissipation of work


- Adiabatic process vs Isentropic process
- If the isentropic process is reversible, it must be adiabatic.
- If the isentropic process is adiabatic, it must be reversible.
- An adiabatic process may not be isentropic because entropy may change due to friction, internal irreversibility etc.
- If the adiabatic process is reversible, it must be isentropic.
- Change in the entropy of a system is due to heat transfer and internal irreversibility (entropy generation.)
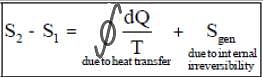
- Entropy is a point function but entropy generation is a path function.
Equation | Holds good for |
dQ = dE+ dW | Reversible, Irreversible, any system |
dQ = dU + dW | Reversible, Irreversible, Closed System. |
dQ = dU + pdf | Reversible, Closed system |
dQ = TdS | Reversible |
TdS = dU + PdV | Reversible, Irreversible, Closed system |
TdS = dH – Vdp | Reversible, Irreversible, Closed system |
- Entropy change of a system (solid, liquid ) when its temperature changes from T1 to T2.

c: specific heat for solid, liquid
|
5 videos|103 docs|59 tests
|
FAQs on Entropy - Mechanical Engineering SSC JE (Technical)
| 1. What is entropy in mechanical engineering? |  |
| 2. How is entropy related to the efficiency of mechanical systems? |  |
| 3. Can entropy be reduced or eliminated in mechanical systems? |  |
| 4. How is entropy calculated in mechanical engineering? |  |
| 5. What are some practical applications of entropy in mechanical engineering? |  |
|
5 videos|103 docs|59 tests
|

|
Explore Courses for Mechanical Engineering exam
|

|



















