Chapter Notes, - Fluid Mechanics, Class 11, Physics (IIT-JEE & AIPMT) PDF Download
FLUID
1. Fluid:
Fluid mechanics deals with the behaviour of fluids at rest and in motion. A fluid is a substance that deforms continuously under the application of a shear (tangential) stress no matter how small the shear stress may be.
Thus, fluids comprise the liquid and gas (or vapor) phase of the physical forms in which matter exists.
Density (r) : Mass of unit volume, Called density
Density at a point of liquid described by

density is a positive scalar quantity.
SI unit = Kg/m3
CGS unit = gm/cm3
Dimension = [ML-3]
Relative Density : It is the ratio of density of given liquid to the density of pure water at 4°C

Relative density or specific gravity is unit less, dimensionless. It is a positive scalar physical Quantity
Value of R.D. is same in SI and CGS system due to dimensionless/unitless
Specific Gravity : It is the ratio of weight of given liquid to the weight of pure water at 4°C
Specific Gravity =  =
=  = Relative density of liquid
= Relative density of liquid
i.e. than specific gravity of a liquid is approximately equal to the relative density. For calculation they can be interchange
2. Pressure in a Fluid
When a fluid (either liquid or gas) is at rest, it exerts a force perpendicular to any surface in contact with it, such as a container wall or a body immersed in the fluid.
While the fluid as a whole is at rest, the molecules that makes up the fluid are in motion, the force exerted by the fluid is due to molecules colliding with their surroundings.
If we think of an imaginary surface within the fluid, the fluid on the two sides of the surface exerts equal and opposite forces on the surface, otherwise the surface would accelerate and the fluid would not remain at rest.
Consider a small surface of area dA centered on a point on the fluid, the normal force exerted by the fluid on each side is  . The pressure P is defined at that point as the normal force per unit area, i.e.,
. The pressure P is defined at that point as the normal force per unit area, i.e.,

If the pressure is the same at all points of a finite plane surface with area A, then

where  is the normal force on one side of the surface. The SI unit of pressure is pascal, where
is the normal force on one side of the surface. The SI unit of pressure is pascal, where
1 pascal = 1 Pa = 1.0 N/m2
One unit used principally in meteorology is the Bar which is equal to 105 Pa.
1 Bar = 105 Pa
2.1 Atmospheric Pressure (P0)
It is pressure of the earth's atmosphere. This changes with weather and elevation. Normal atmospheric pressure at sea level (an average value) is 1.013 × 105 Pa. Thus
1 atm = 1.013 × 105 Pa
Note : Fluid pressure acts perpendicular to any surface in the fluid no matter how that surface is oriented. Hence, pressure has no intrinsic direction of its own, its a scalar. By contrast, force is a vector with a definite direction.
2.2 Variation in Pressure with depth
If the weight of the fluid can be neglected, the pressure in a fluid is the same throughout its volume. But often the fluid's weight is not negligible and under such condition pressure increases with increasing depth below the surface.
Let us now derive a general relation between the pressure P at any point in a fluid at rest and the elevation y of that point. We will assume that the density r and the acceleration due to gravity g are the same throughout the fluid. If the fluid is in equilibrium, every volume element is in equilibrium.

Consider a thin element of fluid with height dy. The bottom and top surfaces each have area A, and they are at elevations y and y + dy above some reference level where y = 0. The weight of the fluid element is
dW = (volume) (density) (g) = (A dy) (r) (g)
or dW = rg A dy
What are the other forces in y-direction of this fluid element ? Call the pressure at the bottom surface P, the total y component of upward force is PA. The pressure at the top surface is P dP and the total y-component of downward force on the top surface is (P dP) A. The fluid element is in equilibrium, so the total y-component of force including the weight and the forces at the bottom and top surfaces must be zero.
åFy = 0
PA -(P + dP) A -rgAdy = 0
or  ...(i)
...(i)
This equation shows that when y increases, P decreases, i.e., as we move upward in the fluid, pressure decreases.
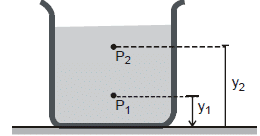
If P1 and P2 be the pressures at elevations y1 and y2 and if r and g are constant, then integrating Eq.(i) , we get

or P2 -P1 = -rg (y2 -y1) ...(ii)
It's often convenient to express Eq. (ii) in terms of the depth below the surface of a fluid. Take point 1 at depth h below the surface of fluid and let P represents pressure at this point. Take point 2 at the surface of the fluid, where the pressure is P0 (subscript zero for zero depth). The depth of point 1 below the surface is,
h = y2 -y1
and Eq. (ii) becomes
P0 -P = -rg (y2 -y1) = -rgh
P = P0 rgh ...(iii)
Thus, pressure increases linearly with dpeth, if r and g are uniform, A graph between P and h is shown below.


Further, the pressure is the same at any two points at the same level in the fluid. The shape of the container does not matter.
2.3. Barometer
It is a device used to measure atmospheric pressure.
In principle, any liquid can be used to fill the barometer, but mercury is the substance of choice because its great density makes possible an instrument of reasonable size.
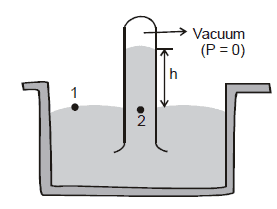
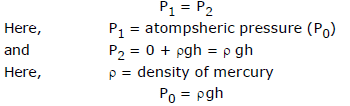
Thus, the mercury barometer reads the atmospheric pressure (P0) directly from the height of the mercury column.
For example if the height of mercury in a barometer is 760 mm, then atmospheric pressure will be,
P0 = rgh = (13.6 × 103) (9.8) (0.760)= 1.01 × 105 N/m2
2.4 Force on Side Wall of Vessel
Force on the side wall of the vessel can not be directly determined as at different depths pressures are different. To find this we consider a strip of width dx at a depth x from the surface of the liquid as shown in figure,
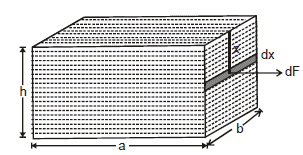
and on this strip the force due to the liquid is given as :
dF = xrg × bdx
This force is acting in the direction normal to the side wall.
Net force can be evaluated by integrating equation

 ...(2.4)
...(2.4)
2.5 Average Pressure on Side Wall
The absolute pressure on the side wall cannot be evaluated because at different depths on this wall pressure is different. The average pressure on the wall can be given as :
 =
=  ...(2.5)
...(2.5)
Equation (2.5) shows that the average pressure on side vertical wall is half of the net pressure at the bottom of the vessel.
2.6 Torque on the Side Wall due to Fluid Pressure
As shown in figure, due to the force dF, the side wall experiences a torque about the bottom edge of the side which is given as
 = xrgb dx (h -x)
= xrgb dx (h -x)
This net torque is 


2.7 Manometer
It is a device used to measure the pressure of a gas inside a container.
The U-shaped tube often contains mercury.
P1 = P2
Here, P1 = pressure of the gas in the container (P)
and P2 = atmospheric pressure (P0) + rgh
P = P0 hrg
This can also be written as
P -P0 = gauge pressure = hrg
Here, r is the density of the liquid used in U - tube
Thus by measuring h we can find absolute (or gauge) pressure in the vessel.
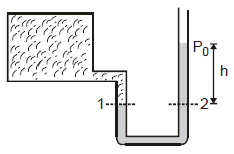
Ex.1 Two liquid which do not react chemically are placed in a bent tube as shown in figure. Find out the displacement of the liquid in equillibrium position.

Sol. The pressure at the interface must be same, calculated via either tube. Since both tube all open to the atmosphere, we must have.

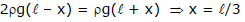
Ex.2 Three liquid which do not react chemically are placed in a bent tube as shown in figure (initially) then fluid out the displacement of the liquid in equillibrium position.

Sol. Let us assume that level of liquid having density 3r displaced below by x as shown in figure below.

⇒ 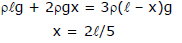
2.8 Pressure Distribution in an Accelerated Frame
We've already discussed that when a liquid is filled in a container, generally its free surface remains horizontal as shown in figure (a) as for its equilibrium its free surface must be normal to gravity i.e. horizontal. Due to the same reason we said that pressure at every point of a liquid layer parallel to its free surface remains constant. Similar situation exist when liquid is in an accelerated frame as shown in figure (b). Due to acceleration of container, liquid filled in it experiences a pseudo force relative to container and due to this the free surface of liquid which normal to the gravity now is filled as
 ...(2.22)
...(2.22)


Now from equilibrium of liquid we can state that pressure at every point in a liquid layer parallel to the free surface (which is not horizontal), remains same for example if we find pressure at a point A in the accelerated container as shown in figure (a) is given as

Where h is the depth of the point A below the free surface of liquid along effective gravity and P0 is the atmospheric pressure acting on free surface of the liquid.


The pressure at point A can also obtained in an another way as shown in figure (b). If l1 and l2 are the vertical and horizontal distances of point A from the surface of liquid then pressure at point A can also be given as
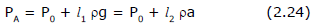
Here l1rg is the pressure at A due to the vertical height of liquid above A and according to Pascal's Law pressure at A is given as
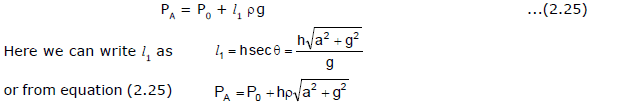
Similarly if we consider the horizontal distance of point A from free surface of liquid, which is l2 then due to pseudo acceleration of container the pressure at point A is given as
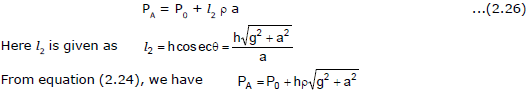
Here students should note that while evaluating pressure at point A from vertical direction we haven't mentioned any thing about pseudo acceleration as along vertical length l1, due to pseudo acceleration at every point pressure must be constant similarly in horizontal direction at every point due to gravity pressure remains constant.
Ex.3 Figure shows a tube in which liquid is filled at the level. It is now rotated at an angular frequency w about an axis passing through arm A find out pressure difference at the liquid interfaces.

Sol. To solve the problem we take a small mass dm from the axis at `a' distance x in displaced condition.
Net inward force = (P +dP) A -PA
= AdP
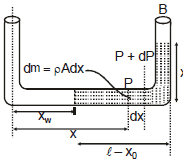
This force is balanced by centripetal force in equilibrium
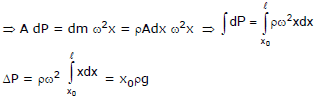
Ex.4 A liquid of density r is in a bucket that spins with angular velocity w as shown in figure.
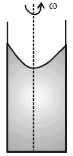
Show that the pressure at a radial distance r from the axis is

where P0 is the atmospheric pressure.
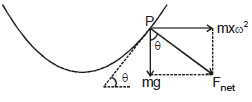
Sol. Consider a fluid particle P of mass m at coordinates
(x, y). From a non-inertial rotating frame of reference two forces are acting on it,
(i) pseudo force (mxw2)
(ii) weight (mg)
in the directions shown in figure.
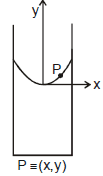
Net force on it should be perpendicular to the free surface (in equilibrium). Hence.
 or
or 


This is the equation of the free surface of the liquid, which is a parabola.
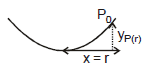
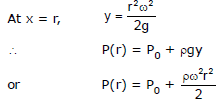
=======================================
Pascal's Principle and Archimedes Principle - Mechanical Properties of Fluids, Class 11, Physics
3. Pascal's Principle
Some times while dealing with the problems of fluid it is desirable to know the pressure at one point is pressure at any other point in a fluid is known. For such types of calculations Pascal's Law is used extensively in dealing of static fluids. It is stated as
"The pressure applied at one point in an enclosed fluid is transmitted uniformly to every part of the fluid and to the walls of the container."
One more example can be considered better to explain the concept of Pascal's Principle. Consider the situation shown in figure, a tube having two different cross section S1 and S2, with pistons of same cross sections fitted at the two ends.

If an external force F1 is applied to the piston 1, it creates a pressure p1 = F1/S1 on the liquid enclosed. As the whole liquid is at the same level, everywhere the pressure in the liquid is increased by p1. The force applied by the liquid on the piston 2 can be given as F2 =p2 × S2, and as the two pistons are at same level p2 = p1. Thus
F2 = p2 × S2
F2 =  ....(2.21)
....(2.21)
Equation (2.21) shows that by using such a system the force can be amplified by an amount equal to the ratio of the cross section of the two pistons. This is the principle of hydraulic press, we'll encounter in next few pages.
3.1 The Hydraulic Lift
Figure shows how Pascal's principle can be made the basis for a hydraulic lift. In operation, let an external force of magnitude F1 be exerted downward on the left input piston, whose area is S1. It result a force F2 which will act on piston 2 by the incompressible liquid in the device.
Here F2 = p2 × S2
And p2 = pB -rgh

Where pB is the pressure on the bottom of the device which can be given as :
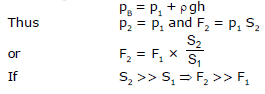
4. Archimedes Principle
If a heavy object is immersed in water, it seems to weight less than when it is in air. This is because the water exerts an upward force called buoyant force. It is equal to the weight of the fluid displaced by the body.
A body wholly or partially submerged in a fluid is buoyed up by a force equal to the weight of the displaced fluid.
This result is known as Archimedes' principle.
Thus, the magnitude of buoyant force (F) is given by,

Here, Vi = immersed volume of solid rL = density of liquid
and g = acceleration due to gravity
Note : Point of Application of buoyant force is center of liquid displaced
Proof
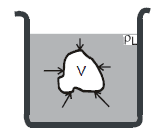
Consider an arbitrary shaped body of volume V placed in a container filled with a fluid of density rL. The body is shown completely immersed, but complete immersion is not essential to the proof. To begin with, imagine the situation before the body was immersed. The region now occupied by the body was filled with fluid, whose weight was  . Because the fluid as a whole was in hydrostatic equilibrium, the net upwards force (due to difference in pressure at different depths) on the fluid in that region was equal to the weight of the fluid occupying that region.
. Because the fluid as a whole was in hydrostatic equilibrium, the net upwards force (due to difference in pressure at different depths) on the fluid in that region was equal to the weight of the fluid occupying that region.
Now, consider what happens when the body has displaced the fluid. The pressure at every point on the surface of the body is unchanged from the value at the same location when the body was not present. This is because the pressure at any point depends only on the depth of that point below the fluid surface. Hence, the net force exerted by the surrounding fluid on the body is exactly the same as the exerted on the region before the body was present. But we know the latter to be  , the weight of the displaced fluid. Hence, this must also be the buoyant force exerted on the body. Archimedes' principle is thus, proved.
, the weight of the displaced fluid. Hence, this must also be the buoyant force exerted on the body. Archimedes' principle is thus, proved.
Ex.5 Beaker cicular cross-section of radius 4 cm is filled with mercury upto a height of 10 cm. Find the force exerted by the mercury on the bottom of the beaker. The atmopheric pressure = 105 N/m2. Density of mercury = 13600 kg/m3. Take g = 10 m/s2
Sol. The pressure at the surface = atmospheric pressure = 105 N/m2.
The pressure at the bottom = 105 N/m2 hrg
= 105 N/m2 + (0.1 m) 

= 105 N/m2 + 13600 N/m2 = 1.136 × 105 N/m2
The force exerted by the mercury on the bottom
= (1.136 × 105 N/m2) × (3.14 × 0.04 m × 004 m) = 571 N
Ex.6 A cubical block of iron 5 cm on each side is floating on mercury in a vessel.
(i) What is the height of the block above mercury level ?
(ii) What is poured in the vessel until it just covers the iron block. What is the height of water column.
Density of mercury = 13.6 gm/cm3
Density of iron 7.2 gm/cm3
Sol. Case-I : Suppose h be the height of cubical block of iron above mercury.
Volume of iron block = 5 ×5 × 5 = 125 cm3
Mass of iron block = 125 × 7.2 = 900 gm
Volume of mercury displaced by the block = 5 × 5 × (5 -h) cm3
Mass of mercury displaced = 5 × 5 (5 -h) × 13.6 gm
By the law floatation,
weight of mercury displaced = weight of iron block
5 × 5 (5 -h) × 13.6 = 900
or (5 -h) =  = 2.65 ⇒ h = 5 -2.65 = 2.35 cm
= 2.65 ⇒ h = 5 -2.65 = 2.35 cm
Case - II : Suppose in this case height of iron block in water be x. The height of iron block in mercury will be (5 -x) cm.


Mass of the water displaced = 5 × 5 × (x) × 1
Mass of mercury displaced = 5 × 5 × (5 -x) × 13.6
So, weight of water displaced weight of mercury displaced = weight of iron block
or 5 × 5 × x × 1 5 × 5 × (5 -x) × 13.6 = 900
or x = (5 -x) × 13.6 = 36
x = 2.54 cm
Ex.7 A tank containing water is placed on spring balanced. A stone of weight w is hung and lowered into the water without touching the sides and the bottom of the tank. Explain how the reading will change.
Sol. The situation is shown in figure.
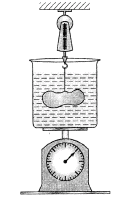
Make free-body diagrams of the bodies separately and consider their equilibrium. Like all other forces, buoyancy is also exerted equally on the two bodies in contact. Hence it the water exerts a buoyant force, say, B on the stone upward, the stone exerts the same force on the water downward. The forces acting on the 'water container' system are : W, weight of the system downward, B, buoyant force of the stone downward, and the force R of the spring in the upward direction. For equilibrium
R = W + B
Thus the reading of the spring scale will increase by an amount equal to the weight of the liquid displaced, that is, by an amount equal to the buoyant force.
Ex.8 A cylindrical vessel containing a liquid is closed by a smooth piston of mass m as shown in figure.
The area of cross-section of the piston is A. If the atmopheric pressure is P0, find the pressure of the liquid just below the prism.
Sol. Let the pressure of the liquid just below the piston be P.
The forces acting on the piston are
(a) its weight, mg (downward)
(b) force due to the air above it, P0A(downward)
(c) force due to the liquid below it, PA (upward)
If the piston is in equilibrium
PA = P0A + mg or P = P0 + 
Ex.9 A rubber ball of mass m and radius r is submerged in water to a depth h released. What height will the ball jump up to above the surface of the water ? Neglect the resistance of water and air.
Sol. Let the ball go up by x above the level of water.
Let us now consider energy conservation between the initial and final positions. In both the positions kinetic energy of the body is zero. The potential energy in the first position with reference to the water level is -mgh plus the work done by an external agent against the buoyant force which is  h,
h,
where r is the density of the water
or x-mgh  h = mgx ⇒
h = mgx ⇒ 
Ex.10 A cube of wood supporting a 200 g mass just floats in water. When the mass is removed, the cube rises by 2 cm. What is the size of the cube ?
Sol. If, l = side of cube, h = height of cube above water and r = density of wood.
Mass of the cube = l3r
Volume of cube in water = l2 (l -h)
Volume of the displaced water = 
As the tube is floating
Ex.11 A boat floating in water tank is carrying a number of large stones. If the stones were unloaded into water, what will happen to water level ? Given the reason in brief.
Sol. Suppose W and w be the weights of the boat and stones respectively.
First, we consider that the boat is floating. It will displaced (W + w) × 1 cm3 of water.
Thus displaced water = (W + w) cm3 [As density of water = 1 gm/cm3]
Secondly, we consider that the stones are unloaded into water.
Now the boat displaces only W × 1 cm3 of water. If r be the density of stones, the volume of water displaced by stones
This shows that the volume of water displaced in the second case is less than the volume of water displaced in the first case. Hence the level of water will come down.
Ex.12 Two solid uniform spheres each of radius 5 cm are connected by a light string and totally immersed in a tank of water. If the specific gravities of the sphere are 0.5 and 2, find the tension in the string and the contact force between the bottom of tank and the heavier sphere.
Sol. The situation is shown in figure
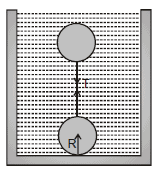
Let the volume of each sphere be V m3 and density of water be r kg/m3.

Similarly
A rod of length 6 m has a mass of 12 kg. If it is hinged at one end at a distance of 3 m below a water surface,
(i) What weight must be attached to other end of the rod so that 5 m of the rod is submerged ?
(ii) Find the magnitude and direction of the force exerted by the hinge on the rod. The specific gravity of the material of the rod is 0.5.
Sol. Let AC be the submerged part of the rod AB hinged at A as shown in figure.
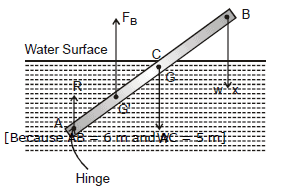
G is the center of gravity of the rod and G¢ is the centre of buoyancy through which force of buoyancy FB acts vertically upwards.
Since the rod is uniform,
The weight of part AC will be  [Because AB = 6 m and AC = 5 m]
[Because AB = 6 m and AC = 5 m]
The buoyance force on rod at G¢ is
 = 20 kg weight
= 20 kg weight
(i) Let x be weight attached at the end B. Balancing torques about A, we get

Negative sign shows that the reaction at the hinge is acting in the downward direction. The magnitude of the reaction is 5.67 kg. wt.
Ex.13 A cylinder of area 300 cm2 and length 10 cm made of material of specific gravity 0.8 is floated in water with its axis vertical. It is then pushed downward, so as to be just immersed. Calculate the work done by the agent who pushes the cylinder into the water.
Sol. Weight of the cylinder = (300 × 10-4) × (10 × 10-2) × 800 kgf = 2.4 kgf
Let x be the length of the cylinder inside the water. Then by the law of floatation
2.4 g = (300 × 10-4 x) × 1000 g
or x = 0.08 m
When completely immersed,
Fb(buoyant force) = (300 × 10-4 × 0.1) × 1000 × g = 3 g N
Thus to immerse the cylinder inside the water the external agent has to push it by 0.02 m against average upward thrust.
Increase in upward thrust = 3g -2.4 g = 0.6 g N
Since this increase in up thrust takes place gradually from 0 to 0.6 g, we may take the average up thrust against which work is done as 0.3 g N.
work done = 0.3 g × 0.02 = 0.0588 J
Ex.14 A piece of an alloy of mass 96 gm is composed of two metals whose specific gravities are 11.4 and 7.4. If the weight of the alloy is 86 gm in water, find the mass of each metal in the alloy.
Sol. Suppose the mass of the metal of specific gravity 11.4 be m and the mass of the second metal of specific gravity 7.4 will be (96-m)
Volume of first metal = 
Volume of second metal = 
Total volume = 
Buoyancy force in water  gm weight
gm weight
Apparent wt. in water = 
According to the given problem,

or 
Solving we get, m = 62.7 gm
Thus mass of second metal is = 96 -62.7 = 33.3 gm
Note : Assumptions of ideal fluid
(1) Fluid is incompressible : density of fluid remain constant through out the fluid.
(2) Fluid is non-viscous : fluid friction is absent
(3) Doesn't show rotational effect : If we release any body in the flowing section there it will not rotate about its C.O.M.
(4) Stream line flow : velocity of fluid at any particular point remains constant with time It may vary with position.
5. Equation of Continuity
This equation defines the steady flow of fluid in a tube. It states that if flow of a fluid is a steady then the mass of fluid entering per second at one end is equal to the mass of fluid leaving per second at the other end.

Figure shown a section of a tube in which at the ends, the cross sectional area are A1 and A2 and the velocity of the fluid are V1 and v2 respectivley.
According to the equation of continuity, if flow is steady mass of fluid entering at end A1 per second = mass of fluid leaving the end A2 per second.
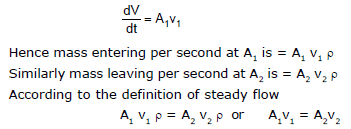
Equation above in known as equation of continuity, which gives that in steady flow the product of cross-section and the speed of fluid everywhere remains constant.
5.1 Freely Falling Liquid
When liquid falls freely under gravity, the area of cross section of the stream continuously decreases, as the velocity increases.

For example, we consider water coming out from a tap, as shown in figure. Let its speed near the mouth of tap is v0 and at a depth h it is v, then we have

If cross section of tap is A then according to the equation of continuity,
the cross section at point M (say a) can be given as
 or
or 
========================================================
Bernoulli's Equation - Fluid Mechanics, Class 11, Physics
6. Bernoulli's Equation
It relates the variables describing the steady laminar of liquid. It is based on energy conservation.
Assumptions
The fluid is incompressible, non-viscous, non rotational and streamline flow.


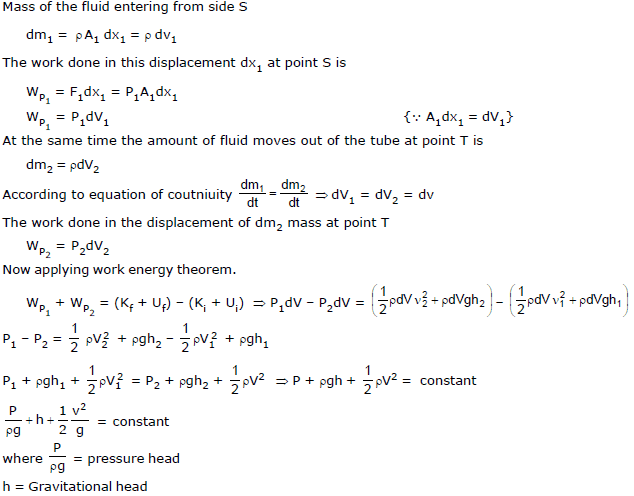
 = volume head
= volume head
6.1 Application of Bernoulli's principle
Magnus effect : When a spinning ball is thrown, it deviates from its usual path in flight. This effect is called Magnus effect and plays an important role in tennis, cricket and soccer, etc., as by applying appropriate spin the moving ball can be made to curve in any desired direction.
If a ball is moving from left to right and also spinning about a horizontal axis perpendicular to the direction of motion as shown in figure, then relative to the ball air will be moving from right to left.



(A) (B) (C)
The resultant velocity of air above the ball will be (V rw) while below it (V -rw) (shown figure). So in accordance with Bernoulli's principle pressure above the ball will be less than below it. Due to this difference of pressure an upward force will act on the ball and hence the ball will deviate from its usual path OA0 and will hit the ground at A1 following the path OA1 (figure shown) i.e., if a ball is thrown with back spin, the pitch will curve less sharply prolonging the flight.
Similarly if the spin is clockwise, i.e., the ball is thrown with top-spin, the force due to pressure difference will act in the direction of gravity and so the pitch will curve more sharply shortening the flight.

Furthermore, if the ball is spinning about a vertical axis, the curving will be side ways as shown in figure. producing the so called out swing or in swing.
Action of Atomiser : The action of aspirator, carburettor, paint-gun, scent-spray or insect-sprayer is based on Bernoulli's principle. In all these by means of motion of a piston P in a cylinder C high speed air is passed over a tube T dipped in liquid L to be sprayed. High speed air creates low pressure over the tube due to which liquid (paint, scent, insecticide or petrol) rises in it and is then blown off in very small droplets with expelled air.

Working of Aeroplane : This is also based on Bernouilli's principle. The wings of the aeroplane are having tapering as shown in figure. Due to this specific shape of wings when the aeroplane runs, air passes at higher speed over it as compared to its lower surface. This difference of air speeds above and below the wings, in accordance with Bernoulli's principle, creates a pressure difference, due to which an upward force called ' dynamic lift' ( = pressure difference × area of wing) acts on the plane. If this force becomes greater than the weight of the plane, the plane will rise up.

Ex.15 If pressure and velocity at point A is P1 and V1 respectively & at point B is P2, V2 is the figure as shown. Comment on P1 and P2.
Sol. From equation of continuity A1V1 = A2V2
here A1 > A2
⇒ V1 < V2 ....(1)
from Bernoulli's equation. We can write

Torricielli's Law of Efflux (Velocity of efflux)
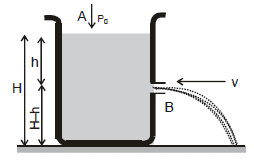
Cross sectional Area of hole at A is greater than B If water is come in tank with velocity vA and going out side with velocity
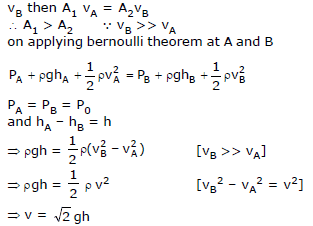
Range (R)
Let us find the range R on the ground.
Considering the vertical motion of the liquid.
(H -h) =  or
or 
Now, considering the horizontal motion,
R = vt or  or
or 
From the expression of R, following conclusions can be drawn,
(i) Rh = RH -h
as  and
and 
This can be shown as in Figure

(ii) R is maximum at  and Rmax = H.
and Rmax = H.
Proof : R2 = 4 (Hh -h2)
For R to be maximum. 
or H -2h = 0 or h = H/2
That is, R is maximum at h=H/2
and  Proved
Proved
Ex.16 A cylindrical dark 1 m in radius rests on a platform 5 m high. Initially the tank is filled with water up to a height of 5 m. A plug whose area is 10-4 m2 is removed from an orifice on the side of the tank at the bottom Calculate (a) initial speed with which the water flows from the orifice (b) initial speed with which the water strikes the ground and (c) time taken to empty the tank to half its original volume (d) Does the time to be emptied the tank depend upon the height of stand.
Sol. The situation is shown in figure
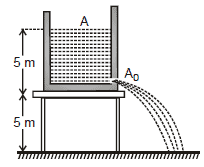
(a) As speed of flow is given by
vH = 
or =  10 m/s
10 m/s
(b) As initial vertical velocity of water is zero,
so its vertical velocity when it hits the ground
 =
= 
 10 m/s
10 m/s
So the initial speed with which water strikes the ground.
 =
=  = 14.1 m/s
= 14.1 m/s
(c) When the height of water level above the hole is y, velocity of flow will be  and so rate of flow
and so rate of flow
 or -Ady =
or -Ady =  A0 dt [As dV = -A dy]
A0 dt [As dV = -A dy]
Which on integration improper limits gives
 ⇒
⇒  So
So  = 9.2 × 103s
= 9.2 × 103s  2.5 h
2.5 h
(d) No, as expression of t is independent of height of stand.
6.1 Venturimeter
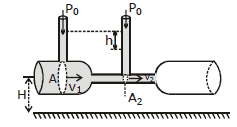
Figure shows a venturimeter used to measure flow speed in a pipe of non - uniform cross-section. We apply Bernoulli's equation to the wide (point 1) and narrow (point 2) parts of the pipe, with h1 = h2

From the continuity equation v2 = 
Substituting and rearranging, we get

Because A1 is greater than A2, v2 is greater than v1 and hence the pressure P2 is less than P1. A net force to the right acceleration the fluid as it enters the narrow part of the tube (called throat) and a net force to the left slows as it leaves. The pressure difference is also equal to rgh, where h is the difference in liquid level in the two tubes. Substituting in Eq. (i), we get

6.2 Pitot Tube
It is a device used to measure flow velocity of fluid. It is a U shaped tube which can be inserted in a tube or in the fluid flowing space as shown in figure shown. In the U tube a liquid which is immiscible with the fluid is filled upto a level C and the short opening M is placed in the fluid flowing space against the flow so that few of the fluid particles entered into the tube and exert a pressure on the liquid in limb A of U tube. Due to this the liquid level changes as shown in figure shown.
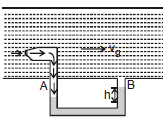
At end B fluid is freely flowing, which exert approximately negligible pressure on this liquid. The pressure difference at ends A and B can be given by measuring the liquid level difference h as
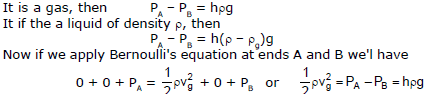
Now by using equations, we can evaluate the velocity v, with which the fluid is flowing.
Note : Pitot tube is also used to measure velocity of aeroplanes with respect to wind. It can be mounted at the top surface of the plain and hence the velocity of wind can be measured with respect to plane.
6.3 Siphon :
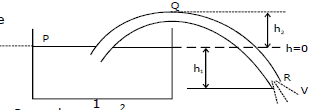
It is a pipe used to drain liquid at a lower height but the pipe initially rises and then comes down
let velocity of outflow is v & the pipe is of uniform cross-section A. Applying bernoulli's equation between P
(top of tank) & R (opening of pipe) we get
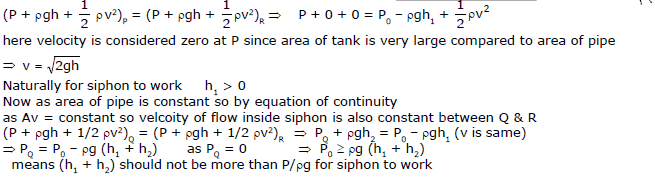
FAQs on Chapter Notes, - Fluid Mechanics, Class 11, Physics (IIT-JEE & AIPMT)
| 1. What is fluid mechanics? |  |
| 2. What are some applications of fluid mechanics? |  |
| 3. What is Bernoulli's principle? |  |
| 4. What is viscosity? |  |
| 5. What is the difference between laminar and turbulent flow? |  |



















