Can You See the Pattern? Class 5 Notes Maths Chapter 7
Patterns
- A pattern is referred to as the arrangement of shapes, numbers, and colours which are in repetition.
- Number patterns, image patterns, logic patterns, word patterns, and so on are all examples of patterns in mathematics.
Image Patterns / Shapes Pattern
- Image Pattern is referred to as the sequence followed by a certain group of objects/shapes.
- For example, In the below image, we can see that the umbrellas follow a pattern. The umbrella is pointing down, then left, then up, and then back to the right. As a result, the following pattern can be observed:
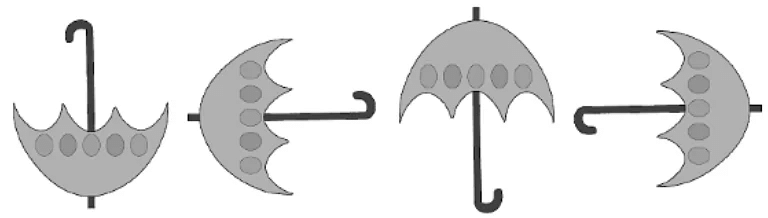
Number Patterns
- A list of numbers follows a specific sequence based on a rule. Such as algebraic or arithmetic, geometric, and the Fibonacci pattern.

Arithmetic or Algebraic Patterns
- Using addition or subtraction we can find the missing number in a sequence.
- The difference between the first and second numbers in the below figure is +3.
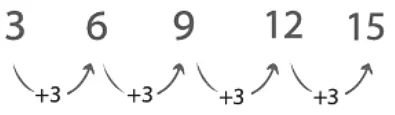
Example: Complete the following number patterns?
5, 10,15 , __, __, __
First Digit = 5
Second Digit = 5 + 5 = 10
Third Digit = 10 + 5 = 15
Clearly, we will add 5 to the preceding digits respectively to find the rest of the digits.
Fourth Digit = 15 + 5 = 20
Similarly , Fifth Digit = 20 + 5 = 25
Sixth Digit = 25 + 5 = 30
Hence the pattern is 5,10,15,20,25,30.
Geometric Series Pattern
- A geometric pattern is a series of numbers formed by multiplying and dividing them.
- Example: Here multiply each term by 2 to get the next term.
2, 4, 8, 16, 32, 64, 128...
Example: Complete the following number patterns?
10, 100,1000 , __, __, __
First Digit = 10
Second Digit = 10 × 10 = 100
Third Digit = 100 × 10 = 1000
Clearly, we will multiply 10 by the preceding digits respectively to find the rest of the digits.
Fourth Digit = 1000 × 10 = 10000
Similarly , Fifth Digit = 10000 × 10 = 100000
Sixth Digit = 100000 × 10 = 1000000
Hence the pattern is 10,100,1000,10000,100000,1000000.
Fibonacci Pattern
- The Fibonacci Pattern is a number sequence in which each consecutive number is obtained by adding the two preceding numbers together.
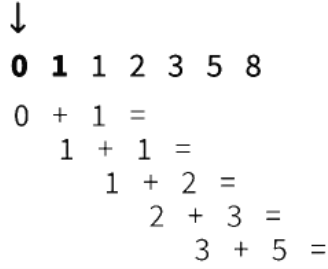
Equal Numbers
- When two or more quantities are exactly the same, we can say they are equal.
- In number patterns, if there is an equal sign(=) in the pattern, then LHS and RHS will have the same numbers.
Examples 1: Find the missing numbers in the following pattern: 10, 20, _ = 10, _, 15.
As you can see, there are two numbers in the LHS: 10 and 20.
And in RHS: 10 and 15
As there is an equal sign it means both sides will have the same numbers.
So the missing numbers in the LHS = 15
And, the missing number in the RHS = 20
Numbers in LHS: 10, 20, 15
Numbers in RHS: 10, 20, 15
Numbers in LHS = Numbers in RHS
Therefore LHS = RHS
Examples 2. Check whether LHS is equal to RHS: 15+ _ + _ = 30 + 20 + 15 ?
As you can see, there are three numbers in the RHS: 30 + 20 + 15.
And in LHS only 15
As there is an equal sign it means both sides will have the same numbers.
So the missing numbers will be the numbers that are in the RHS i.e, 30 and 20
So, missing numbers in LHS will be 15 + 30 + 20
If you add both LHS and RHS we get,
LHS: 15 + 30 + 20 = 65
RHS: 30 + 20 + 15 = 65
Therefore LHS = RHS
Palindrome
- Special words/numbers which remain the same when reversed.
- For example, 99 when reversed remains 99; 101, when reversed, remains 101.
Fun with Odd Numbers
- Integers that do not appear in the table of two are known as odd numbers.
- Note: When we add the first n odd numbers, we will get the sum as n × n, where (n) is the number of odd numbers taken at a time.
Example 1: Let us find the sum of the first 3 odd numbers.
First 3 odd numbers: 1,3, 5. Here n = 3
Adding 1 + 3 + 5 we get 9.
Also, we know that When we add first n odd numbers,
we will get the sum as n × n.
Sum of first 3 odd numbers = n × n i.e. 3 × 3 = 9
So, the Sum of the first 3 odd numbers is 9.
Example 2: Find the sum of the first 6 odd numbers.
First 6 odd numbers: 1, 3, 5, 7, 9, 11. Here n = 6
Adding 1 + 3 + 5 + 7 + 9 + 11 we get 36.
Also, we know that when we add first n odd numbers,
we will get the sum as n × n.
Sum of first 6 odd numbers = n × n i.e. 6 × 6 = 36
So, the Sum of the first 6 odd numbers is 36.
|
31 videos|286 docs|45 tests
|





















