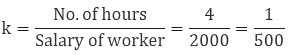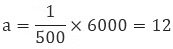Direct and Inverse Proportions Chapter Notes | Mathematics (Maths) Class 8 PDF Download
| Table of contents |

|
| Introduction |

|
| Direct Proportion |

|
| Methods to solve Direct Proportion Problems |

|
| Inverse Proportion |

|
Introduction
There are so many situations in our life where we see some direct or indirect relationship between two things. Like
If the number of things purchased is increasing then the amount to pay will also increase.
If the speeds of the car will increase then the time to reach the destination will decreases.
Variations: If the value of two objects depends upon each other in such a way that the increase or decrease in the value of one object affects the value of another object then these two objects are said to be in variation.
Direct Proportion
Two quantities a and b are said to be in direct proportion if
Increase in a increases the b
Decrease in a decreases the b
But the ratio of their respective values must be the same.
a and b will be in direct proportion if a/b = k(k is constant) or a = kb.
In such a case if b1, b2 are the values of b corresponding to the values a1, a2 of a respectively then, a1/b2 = a2/b1
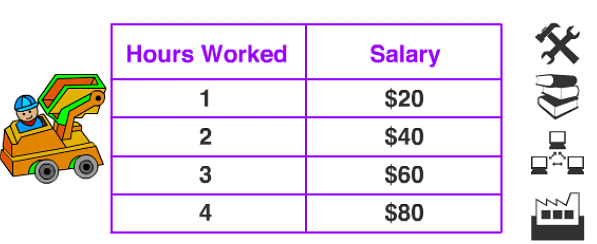
This shows that as the number of hours worked will increase the amount of salary will also increase with the constant ratio.
Example: Suppose a factory produces 150 units of a product in 5 hours. How many units will it produce in 8 hours?
Sol: Look at the following steps:
Identify the direct proportion:
The number of units produced is directly proportional to the number of hours worked. This means that if the number of hours increases, the number of units produced will also increase in the same proportion.Calculate the ratio of hours:
In the first instance, 5 hours are given. In the second instance, 8 hours are given, which is 58=1.6 times the original hours.Apply the same ratio to the units produced:
150 units×1.6=240 units
Since the number of hours increased by 1.6 times, the units produced will also increase by 1.6 times.Conclusion:
So, in 8 hours, the factory will produce 240 units.
Example: Check if x and y are directly proportional:
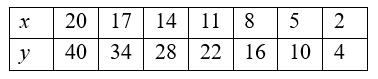
Sol: To determine if x and y are directly proportional, we need to check if the ratio y/x remains constant for all pairs of values.
1. Calculate the ratio for each pair:
- For x and y: y/x = 40/20 = 2
- For x=17 and y=34: y/x = 34/17 = 2
- For x=14 and y=28: y/x = 28/14 = 2
- For x=11 and y=22: y/x = 22/11 = 2
- For x=8 and y=16: y/x = 16/8 = 2
- For x=5 and y=10: y/x = 10/5 = 2
- For x=2 and y=4, y/x = 4/2 = 2
2. Check if the ratios are the same:
The ratio y/x is consistently 2 for all the pairs.
Conclusion:
Since the ratio y/x is constant (always equal to 2), x and y are directly proportional. This means that as x increases or decreases, y changes by the same factor.
Symbol of Proportion

When two quantities a and b are in proportion then they are written as a ∝ b where ∝ represents “is proportion to”.
Methods to solve Direct Proportion Problems
There are two methods to solve the problems related to direct proportion-
1. Tabular Method
As we know that,
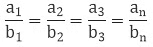
so, if one ratio is given then we can find the other values also. (The ratio remains the constant in the direct proportion).
Example: The cost of 4-litre milk is 200 Rs. Tabulate the cost of 2, 3, 5, 8 litres of milk of same quality.
Sol: Let X litre of milk is of cost Y Rs.
We know that as the litre will increase the cost will also increase and if the litre will decrease then the cost will also decrease.
Given,
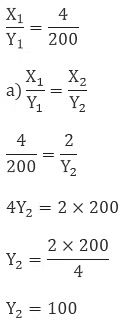
So the cost of 2 ltr milk is 100 Rs.
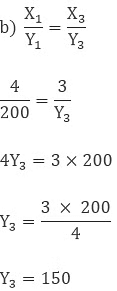
So the cost of 3 ltr milk is 150 Rs.
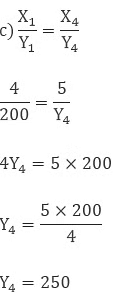
So the cost of 5 ltr milk is 250 Rs.
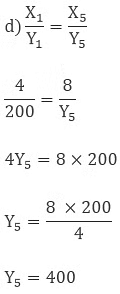
So the cost of 8 ltr milk is 400 Rs.
2. Unitary Method
If two quantities a and b are in direct proportion then the relation will be
k = a/b or a = kb
We can use this relation in solving the problem.
Example: If a worker gets 2000 Rs. to work for 4 hours then how much time will they work to get 60000 Rs.?
Sol: Here,
By using this relation a = kb we can find
Hence, they have to work for 12 hours to get Rs 60000
Inverse Proportion
Two quantities a and b are said to be in Inverse proportion if
Increase in a decreases b
Decrease in a increases b
But the ratio of their respective values must be the same.
a and b will be in inverse proportion if k= ab
In such a case if b1, b2 are the values of b corresponding to the values a1, a2 of a respectively then, a1b1 = a2b2 = k,
When two quantities a and b are in inverse proportion then they are written as a ∝ 1/b

This shows that as the distance of the figure from light increases then the brightness to the figure decreases.
Example: If 15 artists can make a statue in 48 hours then how many artists will be required to do the same work in 30 hours?
Sol: Let the number of artists required to make a statue in 30 hours be y.
We know that as the no. of artists will increase the time to complete the work will reduce. So, the number of hours and number of artists are in inverse proportion.
So 48 × 15 = 30 × y (a1b1 = a2b2)
Therefore,
So, 24 artists will be required to make the statue in 30 hours.
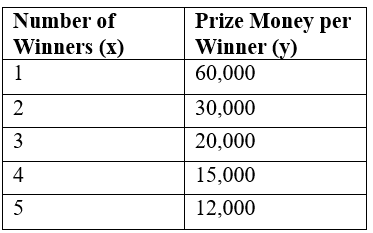
Example: In a contest, a total prize of ₹60,000 is to be divided equally among the winners. Complete the following table and determine whether the prize money per winner is directly or inversely proportional to the number of winners.
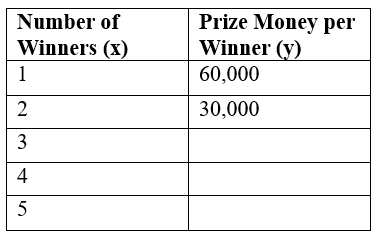
Sol:
1. Calculate the prize money per winner:
When there is 1 winner:
Prize money per winner = 60,000/1 = 60,000When there are 2 winners:
Prize money per winner = 60,000/2 = 30,000When there are 3 winners:
Prize money per winner = 60,000/3 = 20,000When there are 4 winners:
Prize money per winner = 60,000/4 = 15,000When there are 5 winners:
Prize money per winner = 60,000/5 = 12,0002. Complete the table:
3. Determine if the relationship is direct or inverse proportionality:
- To check for direct proportionality, the ratio y/x should be constant.
- To check for inverse proportionality, the product x*y should be constant.
4. Check the product x*y:
- For 1 winner: 1×60,000=60,000
- For 2 winners: 2×30,000=60,000
- For 3 winners: 3×20,000=60,000
- For 4 winners: 4×15,000=60,000
- For 5 winners: 5×12,000=60,000
Conclusion:
The prize money per winner is inversely proportional to the number of winners because the product x*y remains constant. This means that as the number of winners increases, the prize money per individual decreases proportionally.
|
81 videos|423 docs|31 tests
|
FAQs on Direct and Inverse Proportions Chapter Notes - Mathematics (Maths) Class 8
| 1. What is direct proportion? |  |
| 2. How can you identify if two quantities are in direct proportion? |  |
| 3. What is inverse proportion? |  |
| 4. How do you distinguish between direct and inverse proportion? |  |
| 5. Can a quantity be in both direct and inverse proportion at the same time? |  |