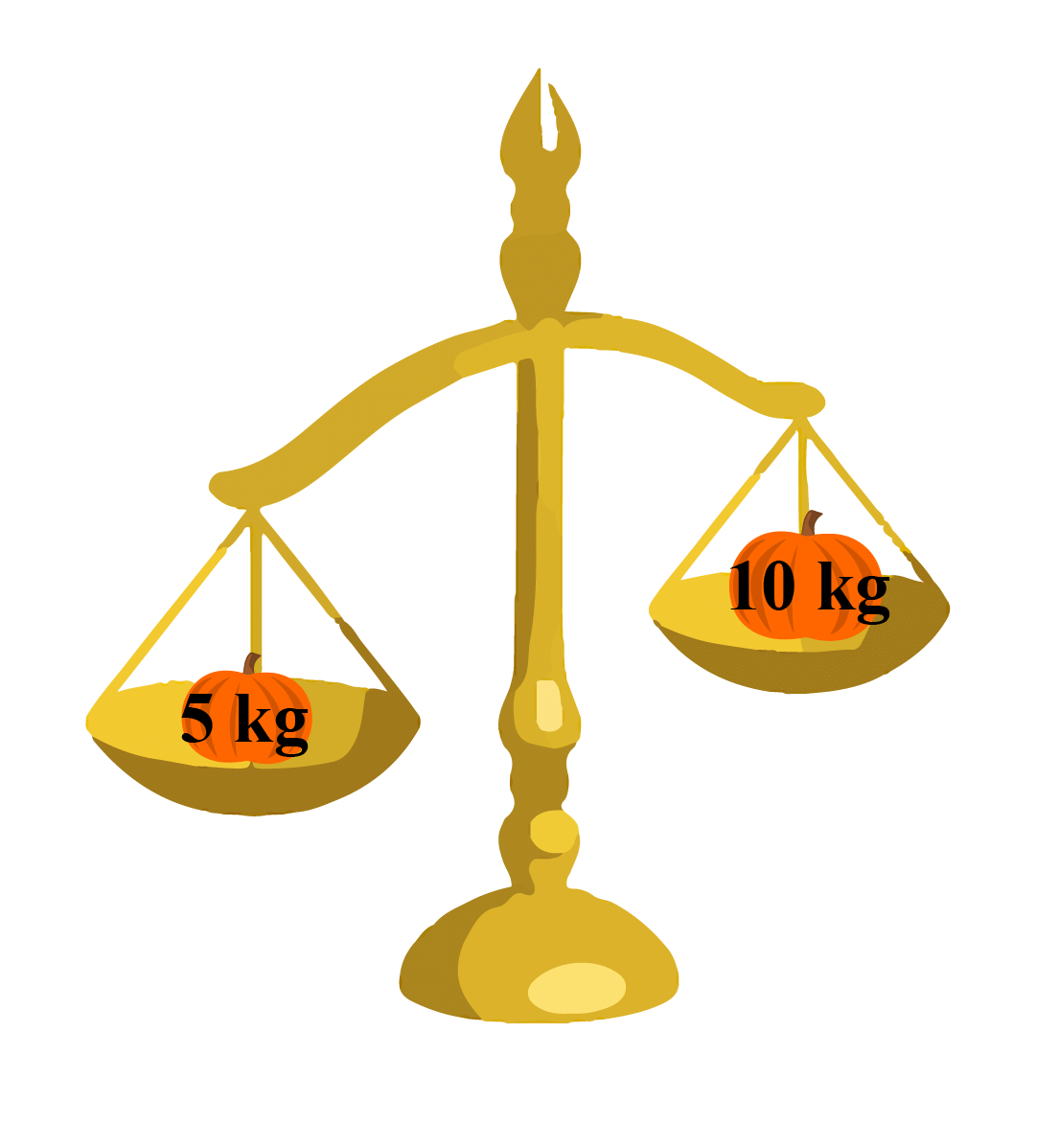Halves and Quarters Chapter Notes | Mathematics for Class 4: NCERT PDF Download
| Table of contents |

|
| Introduction |

|
| Halves |

|
| Quarters |

|
| Different forms of Quadrant and Halves |

|
| Half and Quarter of a Meter |

|
| Sharing Milk |

|
| Balance the Weight |

|
| Why is it Wrong |

|
Introduction
Today, we're diving into the exciting world of fractions, specifically halves and quarters. Fractions may sound complex, but don't worry, we'll make them super easy to understand .Imagine you have a delicious pizza sitting in front of you. Now, what if I told you we could share that pizza equally among friends using halves and quarters? That's right! Halves and quarters are like magic tools that help us divide things into equal parts.
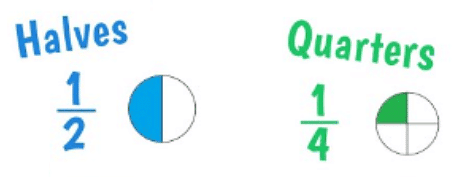
Halves
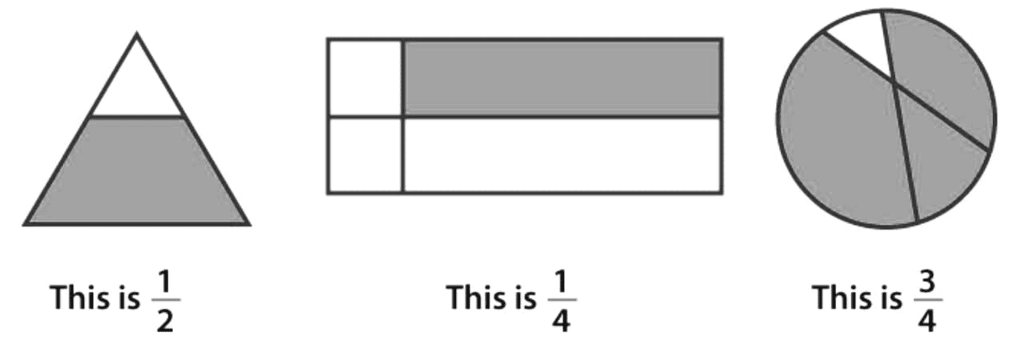
When we talk about Halves, we're essentially dividing something into two equal parts. Imagine you have a whole pizza. If you cut it exactly in the middle, you'd have two halves. Each half is equal in size and represents 1/2 of the pizza. In mathematical terms, "1/2" represents one of those equal parts. Another way to think about it is if you have a whole number, like 2, dividing it by 2 gives you 1, which is half of 2.
Quarters
Quarters take the concept of halves a step further by dividing something into four equal parts. Picture the same pizza again. If you cut it into four equal slices, each slice is a quarter of the pizza. Each quarter represents 1/4 of the pizza. In math, "1/4" signifies one of those equal parts. You can also think of it as taking something whole, like 4, and dividing it into 4 equal parts, each part being 1.

Different forms of Quadrant and Halves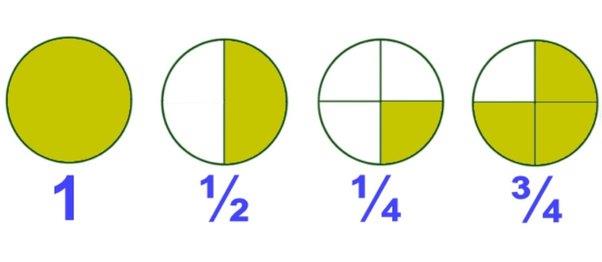
These fractions represent different parts of a whole. "1/4" signifies one part out of four equal parts, like having one slice of a pizza out of four. "2/4" represents two parts out of four, essentially the same as half, like having two slices out of four. "3/4" indicates three parts out of four, like having three slices out of four in a pizza. Finally, "1" on its own represents the entirety or one whole unit, like having the entire pizza or pie.
Half and Quarter of a Meter
Half of a Meter (1/2 meter): This is half of the length of a meter. In practical terms, it's equivalent to 50 centimeters (since there are 100 centimeters in a meter). So, if you have a meter stick and you measure 50 centimeters from one end, you've found half of a meter.
Quarter of a Meter (1/4 meter): This is one-fourth of the length of a meter. Since a meter is divided into 100 centimeters, one-fourth of it would be 25 centimeters. So, if you measure 25 centimeters from one end of the meter stick, you've found a quarter of a meter.
Sharing Milk
Sharing in Quarters: If you want to share the milk equally among four friends, you can divide the liter of milk into four equal parts, or quarters. Each quarter would be 1/4 of the liter. So, you would pour 250 milliliters (1/4 of a liter) into each person's glass. This way, everyone gets an equal share, and you've effectively divided the milk into quarters.
Sharing in Halves: Now, let's say you only have two friends to share the milk with. You can divide the liter of milk into two equal parts, or halves. Each half would be 1/2 of the liter. So, you would pour 500 milliliters (1/2 of a liter) into each person's glass. Again, everyone gets an equal share, and you've divided the milk into halves.
Balance the Weight
Balancing weights using halves and quarters involves distributing weight equally on both sides of a scale. With halves, you ensure each side carries half the weight; for example, a 1-kilogram weight on one side matches with another 1-kilogram weight on the other. With quarters, each side carries a quarter of the weight; for instance, a 2-kilogram weight on one side matches with two 1-kilogram weights on the other. This balance ensures equilibrium and is essential in various contexts like cooking, science, and commerce.
Why is it Wrong
"Wrong halves" and "wrong quarters" refer to situations where items are divided into unequal parts, despite being intended to be divided equally. These terms are used when the division is incorrect or when the parts are not truly equal.
|
26 videos|142 docs|34 tests
|