Lines and Angles Class 9 Notes Maths Chapter 6
Introduction to Lines and Angles
We see lines and angles all around us in different objects. In our daily life, we come across different types of angles formed between the edges of different surfaces.
 An architect applies the knowledge of lines and angles for drawing a plan of a multi-storied building.
An architect applies the knowledge of lines and angles for drawing a plan of a multi-storied building.
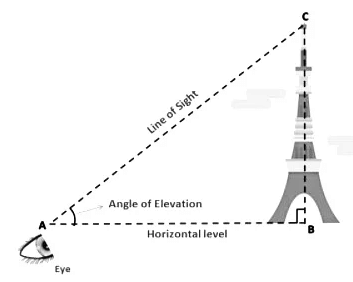
In science, lines are extensively used to represent the properties of light using the ray
diagrams. We can easily find the height of a tower or a tall building if we know the angle formed between the horizontal line and the line of sight.
Basic Terms and Definitions
- Line: It is a collection of points which has only length, no breadth or thickness and is endless in both directions. Line AB is denoted by


- Line segment: A portion of a line with two endpoints is called a line segment. Line segment AB is denoted by


- Ray: A part of a line with one endpoint is called a ray. Ray AB is represented by


- Collinear Points: If three or more points lie on the same line, they are called collinear points otherwise they are called non-collinear points.

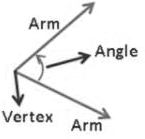
- Angle: When two rays originate from the same endpoint, they form an angle. The rays making an angle are called the arms and the endpoint is called the vertex of the angle.

Types of Angles
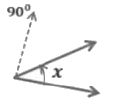
- Acute Angle is an angle whose measure is more than 0°but less than 90°
0° < x < 90°
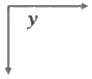
- A right angle is an angle whose measure is90°.
y = 90°
- An obtuse angle is an angle whose measure is greater than 90° but less than 180°.
90° < z < 180°
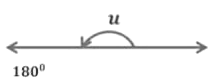
- A straight angle is an angle whose measure is 180°. Thus, a straight angle looks like a straight line.
u = 180°
- A reflex angle is an angle whose measure is more than 180° but less than 360°
180° < v < 360°
Complementary and Supplementary Angles
A pair of angles are said to be complementary if the sum of the angles is equal to 90°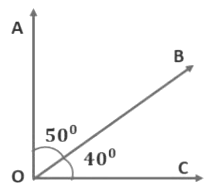
∠AOB + ∠BOC =50° + 40° = 90°
∠AOB + ∠BOC =90°
∴∠AOB and ∠BOC are complementary angles.
A pair of angles are said to be supplementary if the sum of the angles is equal to 180°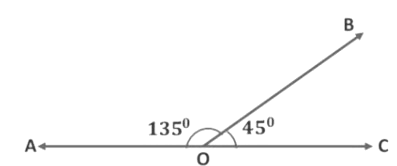
∠AOB + ∠BOC = 135° + 45° = 180°
∠AOB + ∠BOC= 180°
∴ ∠AOB and ∠BOC are supplementary angles.
Example 1: If (2x − 20°) and (x + 5°) are complementary angles, find the angles.
A pair of angles is said to be complementary if the sum of the angles is equal to 90°.
If (2x − 20°)and (x + 5°) are complementary angles then their sum will be equal to 90°.
(2x − 20°) + (x + 5°) = 90°
2x − 20° + x + 5° = 90°
2x + x − 20° + 5° = 90
3x − 15° = 90° ⇒ 3x = 15° + 90°
3x = 105° ⇒ x = 105°/3 = 35°
(2x − 20°) = (2 × 35° − 20°) ⇒ 70° − 20° = 50°
(2x − 20°) = 50°
(x + 5°) = 35° + 5° = 40°
(x + 5°) = 40°
Example 2: Two supplementary are in the ratio 3: 6, find the angles.
Let the two supplementary angles be 3x and 6x,
3x + 6x = 180°A pair of angles are said to be supplementary if the sum of the angles is equal to 180°
9x = 180°⇒ x = 180/9 = 20°
x = 20°
3x = 3 × 20 = 60°
6x = 6 × 20° = 120°
Adjacent Angles
Two angles are adjacent if
(i) they have a common vertex
(ii) they have a common arm
(iii) their non-common arms are on different sides of the common arm.
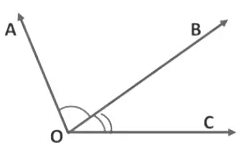
Here, ∠AOB and ∠BOC are adjacent angles because these angles have a common vertex O. Ray OB is the common arm. Rays AO and CO are the non-common arms.
When two angles are adjacent, then their sum is always equal to the angle formed by the two non–common arms.
Therefore, ∠AOC = ∠AOB + ∠BOC
We see that ∠AOC and ∠AOB are not adjacent as their non-common arms OB and OC are on the same side of the common arm AO.
Linear pair of Angles
If the non-common arms of two adjacent angles are two opposite rays, then these angles are called linear pairs of angles.
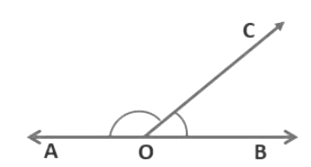
Here, OA and OB are two opposite rays and ∠AOC, ∠BOC are adjacent angles.
Therefore, ∠AOC and ∠BOC form a linear pair.
Vertically Opposite Angles
When two lines AB and CD intersect each other at point O, then there are two pairs of vertically opposite angles.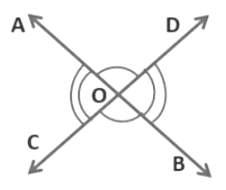
Here,
(i) ∠ AOC and ∠ BOD are vertically opposite angles.
(ii) ∠ AOD and ∠ BOC are vertically opposite angles
Intersecting and non-intersecting lines
Intersecting Lines: Two lines are said to be intersecting when the perpendicular distance between the two lines is not the same everywhere and they intersect at one point.
Here, lines AB and CD are intersecting lines.
Non-Intersecting Lines
Two lines are said to be non–intersecting when the perpendicular distance between them is the same everywhere and they do not meet.
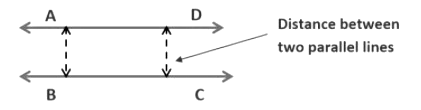
The lengths of the common perpendiculars at different points on these lines are the same and so these lines are parallel. This equal length is called the distance between two parallel lines.
Two lines in a plane will either intersect at one point or do not intersect at all, that is they are parallel.
Pairs of Angles
Axiom 1: If a ray stands on a line, then the sum of two adjacent angles so formed is 180°.
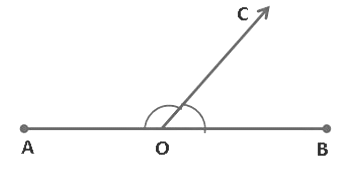
Here, ray OC stands on line AB, then ∠AOC and ∠COB are adjacent angles.
Therefore, ∠AOC + ∠COB = 180°
In Axiom 1, it is given that a ray stands on a line and we concluded that the sum of two adjacent angles so formed is 180°. Now, if we do the reverse and take the ‘conclusion’ of Axiom 1 as ‘given’ and ‘given’ as ‘conclusion’ then it becomes:
Statement A: If the sum of two adjacent angles is 180° then a ray stands on a line.

We see that Axiom 1 and Statement A are converse of each other.
If we place a ruler along with one of the non-common arms we see that the other non-common arm also lies along the ruler.
Therefore, points A, O and B lie on the same line and ray OC stands on it.
∠ AOC + ∠COB = 115°+ 65°= 180°
Therefore, statement A is true.
The given statement can be stated in the form of an axiom as follows:
Axiom 2: If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line.
Axiom 1 and 2, together are called the linear pair axiom.
Theorem 1: If two lines intersect each other, then the vertically opposite angles are equal.
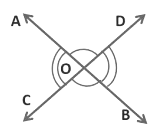
Given: Lines AB and CD intersect each other at point O. So, two pairs of vertically opposite angles are formed,
i) ∠ AOC and ∠BOD
ii) ∠ AOD and ∠COB
To prove: ∠AOC = ∠BOD and ∠AOD=∠COB
Proof: Here, ray AO stands on line CD.
∴ ∠AOC +∠AOD = 180°
(by Linear Pair axiom) ..... (1)
Similarly, ray DO stands on line AB.
∴ ∠AOD+∠BOD = 180° (by Linear Pair axiom) ..... (2)
Using Eq 1 and 2 we get,
∠AOC +∠AOD = ∠AOD+∠BODSubtracting ∠AOD from both sides we get,
∠AOC +∠AOD - ∠AOD = ∠AOD+∠BOD - ∠AOD
(Euclid’s axiom 3 states that if equals are subtracted from equals, the remainders are equal)
∠AOC +∠AOD - ∠AOD = ∠BOD + ∠AOD - ∠AOD
∴ ∠ AOC = ∠ BOD
Now, we know ray AO stands on line CD.
∴ ∠AOC +∠AOD = 180°
(by Linear Pair axiom) ..... (1)
Similarly, ray CO stands on line AB.
∴ ∠AOC+∠BOC = 180°
(by Linear Pair axiom) ..... (2)
Using Eq 1 and 2 we get,
∠AOC +∠AOD = ∠AOC+∠BOC
Subtracting ∠AOC from both sides we get,
∠AOC +∠AOD - ∠AOC = ∠AOC+∠BOC - ∠AOC
(Using Euclid’s axiom 3 states which that if equals are subtracted from equals, the remainders are equal)
∠AOD + ∠AOC - ∠AOC = ∠BOC + ∠AOC- ∠AOC∴ ∠ AOD = ∠ BOC
We see that two pairs of vertically opposite angles are equal.
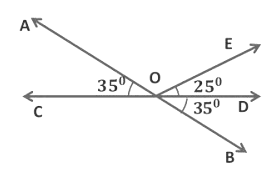
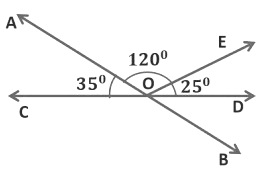
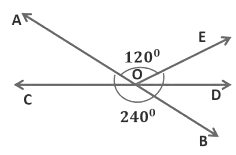
Example 1: In the given figure AB and CD intersect at O. If ∠AOC+∠DOE = 60° and ∠BOD = 35°, find ∠DOE and reflex ∠AOE.
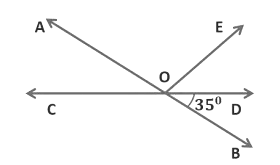
We know,
(i) ∠AOC + ∠DOE = 60°
(ii) ∠BOD = 35°
Here, lines AB and CD intersect each other at O.
So, ∠AOC = ∠BOD = 35°
(If two lines intersect each other, then the vertically opposite angles are equal)
∠AOC + ∠DOE = 60°
35° + ∠DOE = 60°
(∵ ∠AOC = 35°)
∠DOE = 60° − 35° = 25°
∠DOE = 25°
We see that COD is a straight line, that is the measure of the ∠COD is equal to 180°.
∠AOC+ ∠AOE +∠EOD = 180°
∠AOE + (∠AOC+ ∠EOD) = 180°
∠AOE + 60°= 180°
(∵ ∠AOC + ∠DOE = 60°)
∠AOE = 180° - 60°
∠AOE =120°
Reflex ∠ AOE = 360°- 120°= 240°
(reflex angle is an angle whose measure is greater than 180° but less than 360°)
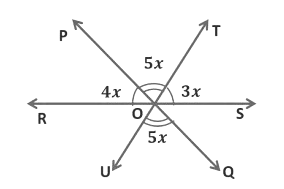
Example 2: In the figure given below, lines PQ, RS and TU meet at point O. Find the value of x, hence find all the three indicated angles.
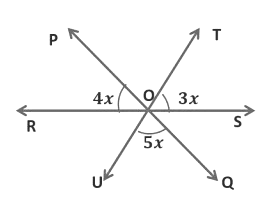
Here, lines PQ and TU intersect each other at O.
So, ∠POT = ∠UOQ = 5x (If two lines intersect each other, then the vertically opposite angles are equal)We see that ROS is a straight line, that is the measure of the ∠ROS is equal to 180°.
∠ROP+ ∠POT +∠TOS = 180°
4x + 5x + 3x = 180°
12x = 180°
x = 180°/12
x = 15°
∠POR = 4x = 4 × 15° = 60°
∠UOQ = 5x = 5 × 15° = 75°
∠TOS = 3x = 3 × 15° = 45°
Example 3: Lines AB and CD intersect each other at O. If ∠AOD:∠AOC = 2: 4, find all the angles x, y and z .
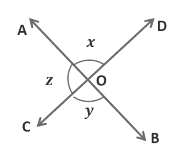
We know,
∠AOD : ∠AOC = 2 : 4
Let, ∠AOD = 2a and ∠AOC = 4a
Ray AO stands on line CD.
∠AOD +∠AOC = 180°(If a ray stands on a line, then the sum of two adjacent angles so formed is 1800 )
2a + 4a = 180°
6a = 180°
a = 180°/6 = 30°
∠ AOD = x = 2a = 2 × 30°= 60°
∠ AOC = z = 4a = 4 × 30°= 120°
x = y = 60° (Vertically opposite angles are equal)
So, x = 60°, y = 60° and z = 120°
Lines parallel to the same line
If two lines are parallel to the same line then they are parallel to each other.
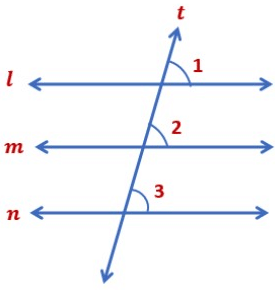
We draw a transversal t for the lines l, m and n, where line l is parallel to line n and line m is parallel to line n.
Now,
∠1 = ∠3(corresponding angles axiom) → Eq 1
Similarly, ∠2 = ∠3 (corresponding angles axiom) → Eq 2
Using Eq 1 and 2 we get, ∠1 = ∠2
∠1 and ∠2 are corresponding angles.
The converse of corresponding angles axiom states that if a transversal intersects two lines such that a pair of corresponding angles are equal, then the two lines are parallel to each other
Therefore, line l is parallel to line m ( l || m )
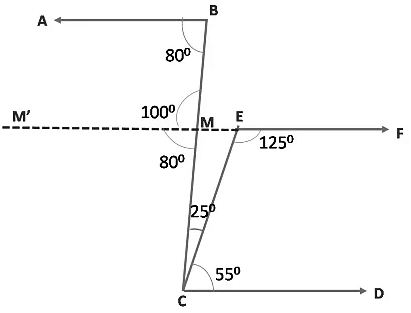
Example 1: In the given figure, show that AB || CD.
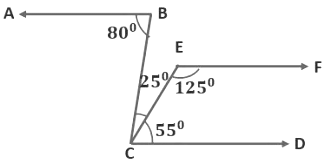
∠BCD = ∠BCE + ∠ECD
∠BCD = 25° + 55° = 80°
We see that ∠ABC and ∠BCD are alternate interior angles.
∠ABC = ∠BCD = 80°
If a transversal intersects two lines such that a pair of alternate interior angles are equal, then the two lines are parallel.
∴ AB ||CD
OR
∠ FEC + ∠ECD = 125° + 55° = 180°
If a transversal intersects two lines, in such a way that each pair of interior angles on the same side of the transversal is supplementary, then the lines are parallel.
∴ CD ||EF......... (1)
Now let us extend EF till it intersects BC at M and extend it till M’.
Then since CD ||EF
We can find the remaining angles.
The remaining angles are as shown:Now,
∠ CMM’ = ∠ DCM = 80° – (Interior alternate angles)
∠ BMM’ + ∠ CMM’ = 18° – Linear Pair of angles
∠ BMM’ = 100°
∠ BMM’ + ∠MBA = 100° + 80° = 180°
If a transversal intersects two lines, in such a way that each pair of interior angles on the same side of the transversal is supplementary, then the lines are parallel.
∴ AB ||EF......... (2)
From eq (1) and (2), we get
AB ||CD
Example 2: In the figure p||q||r. From the figure, find the ratio of (a + b): (b − a).
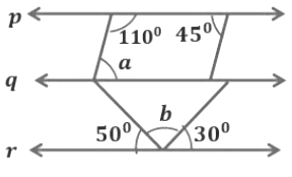
50° + b + 30° = 180°
b + (50° + 30°) = 180°
b + 80° = 180°
b = 180° − 80°
b = 100°
We know that p||q .If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
So, 110° + a = 180°
a = 180° − 110° = 70°
a = 70°
a + b = 70° + 100° = 170°
b − a = 100° − 70° = 30°
(a + b) : ( b − a) = 170°: 30°= 17°∶ 3°
Example 3: In the figure, PQ||RS, RS||TU, and TP⊥ PQ. If ∠STU = 65°, find the value of a, b and c.
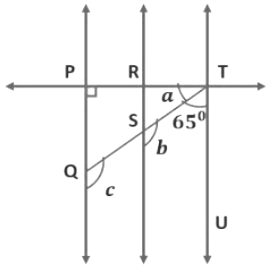
We know, PQ||RS, RS||TU, and TP⊥ PQ.
∠ STU = 65°
b + 65° = 180°
(If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary)
b = 180° − 65° = 115°
b = c = 115° (corresponding angles)
a + 65° = 90° (∵ TP⊥ PQ)
a = 90° − 65° = 25°
So,a = 25°, b = c = 115°
Angle sum property of a triangle (Old Syllabus)
We know that the sum of all the angles of a triangle is 180°.
A triangle is a plane figure formed by three intersecting lines.
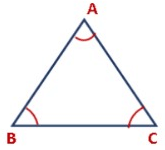

- ∠A, ∠B, and ∠C are called interior angles of the triangle.
- When side BC is produced to D then we get an exterior angle,∠ACD.
- ∠BAC and ∠ABC are called its interior opposite angles.
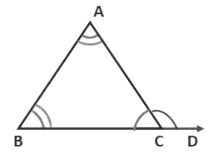
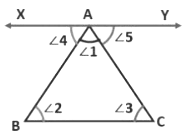
Theorem 1: The sum of the angles of a triangle is 180°
Here, ∠1, ∠2 and ∠3 are the angles of ∆ABC.
To prove: ∠1 + ∠2 + ∠3 = 180°Construction: We draw a line XAY parallel to BC through the vertex A. (If we draw parallel lines then we can use the properties of parallel lines)
Here, XAY is a straight line.
∴ ∠4 + ∠1 + ∠5 = 180° → Eq 1
We see that XAY is parallel to BC, so, AB and AC are transversals.
So, ∠4 = ∠2 (Alternate Angles)
∠3 = ∠5 (Alternate Angles)
Putting∠4 = ∠2, and ∠3 = ∠5 in Eq 1 we get,
∠2 + ∠1 + ∠3 = 180° → Eq 2
∠1 + ∠2 + ∠3 = 180°
Thus, the sum of three angles of a triangle is 180°.
Theorem 2: If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
In ∆ABC, side BC is produced to D to form the exterior angle, ∠ACD.
To prove: ∠A + ∠B = ∠ACD
In ∆ABC,
∠A + ∠B + ∠ACB = 180° (Angle sum property of triangle) → Eq 1
Here, BCD is a straight line.
∴ ∠ACB + ∠ACD = 180° → Eq 2
From Eq 1 and 2 we get,
∠A + ∠B + ∠ACB = ∠ACB + ∠ACD
Subtracting ∠ACB from both sides we get,
∠A + ∠B + ∠ACB - ∠ACB = ∠ACB + ∠ACD - ∠ACB
∠A + ∠B + ∠ACB - ∠ACB = ∠ACB - ∠ACB+ ∠ACD
∠A + ∠B = ∠ACD
Thus, the exterior angle is equal to the sum of the two interior opposite angles.
Example 1: The measure of the exterior angle, ∠PRS of ∆PQR is 100°.If one of the interior angles is 20°, find the measure of the other two angles of ∆PQR.
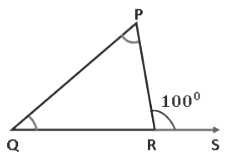
Exterior angle, ∠PRS = 100°
One of the interior angles = 20°
Let ∠Q = 20°
then the other interior opposite angle will be ∠P.
So,∠PRS = ∠Q + ∠P (exterior angle of a triangle is equal to the sum of the two interior opposite angles)
100° = 20° + ∠P
∠P = 100° − 20° = 80°
Now, ∠P + ∠Q + ∠PRQ = 180°
(Angle sum property of triangle states that the sum of the angles of a triangle is 180°)
80° + 20° + ∠PRQ = 180°
100° + ∠PRQ = 180°
∠PRQ = 180° − 100°
∠PRQ = 80°
Therefore, the measures of the three angles of ∆PQR are
∠P = 80°
∠Q = 20°
∠PRQ = 80°
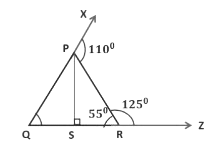
Example 2: In the figure given below, PY || SZ, PS ⊥ QR, and PY bisect∠XPR. If ∠XPR = 110° then find the measure of ∠PQR and ∠PRZ.
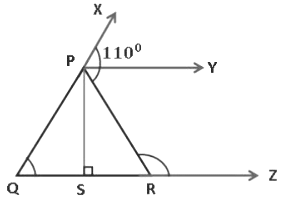
Now, ∠XPR = 110°
∠XPY = ∠YPR (∵ PY is the bisector which bisects ∠XPR)
∴ ∠XPY = ∠YPR = 110°/2 = 55°We know that PY is parallel to SZ.
∠YPR = ∠PRS = 55° (alternate angles)
Here, SRZ is a straight line.
∴ ∠ PRS + ∠PRZ = 180°
55°+ ∠PRZ = 180°
∠PRZ = 180°- 55°
∠PRZ = 125°Now, ∠ XPR = ∠PRQ + ∠PQR
(exterior angle of a triangle is equal
to the sum of the two interior opposite angles)
110° = 55° + ∠PQR
∠PQR = 110° − 55° = 55°
∠PQR = 55° and ∠PRZ = 125°
Example 3: In the figure given below, PR || QS. If ∠PRS = 50° and ∠SUT = 30° then find ∠STU.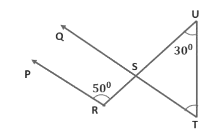
We know, PR||QS and so ∠PRQ and ∠QSU are a pair of corresponding angles.
∴ ∠PRQ = ∠QSU =50°We see that ∠QSU is an exterior angle of the ∆ STU.
∠QSU = ∠SUT + ∠STU (exterior angle of a triangle is equal to the sum of the two interior opposite angles)
50° = 30° + ∠STU
∠STU = 50° − 30° = 20°
∠STU = 20°
Example 4: In the figure, ∠BPC = 40°, ∠ABQ = 65° and lines m and n are parallel to each other. Find x, y, and z.
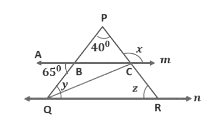
∠ABQ = ∠PBC = 65° (Vertically opposite angle)
Here, x is an exterior angle of ∆PBC.
∴ x = ∠PBC + ∠BPC
x = 65° + 40° = 105°Line m || line n.
So, ∠ABQ = ∠BQC = y = 65° (Alternate angles)
In ∆ PQR,
∠P + ∠ Q + ∠R = 180°(Angle sum property of triangle states that the sum of the angles of a triangle is 180°)
40° + y + z = 180°
40° + 65° + z = 180°
105° + z = 180°
z = 180° − 105°= 75°
x = 105°, y = 65° and z = 75°
Parallel Lines and Transversal Lines (Old Syllabus)
If two lines in the same plane do not intersect, when produced on either side, then such lines are said to be parallel to each other.
Here, lines l and m are parallel to each other.
A line that intersects two or more straight lines at distinct points is called a transversal line.
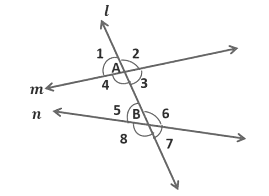
Here, line l intersects lines m and n at points A and B respectively.
We see that four angles are formed at each point A and B, namely
∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8.
The pairs of angles formed, when a transversal intersects two lines are as follows:

- Corresponding Angles: The angles on the same side of a transversal are known as corresponding angles if both lies either above or below the lines.
∠1 & ∠5
∠2 & ∠6
∠4 & ∠8
∠3 & ∠7 - Alternate Interior Angles: The pairs of interior angles on opposite sides of the transversal are called alternate interior angles.
∠4 & ∠6
∠3 & ∠5 - Alternate Exterior Angles: The pairs of exterior angles on opposite sides of the transversal are called alternate exterior angles.
∠1 & ∠7
∠2 & ∠8 - Interior angles on the same side of the transversal: They are also referred to as consecutive interior angles or allied angles or co-interior angles.
∠4 & ∠5
∠3 & ∠6
Here, we see that the lines m and n are not parallel. Can you tell what will happen if line l intersects two parallel lines m and n?
When a transversal l intersects two parallel lines m and n, then the relation between angles formed are obtained as axioms and theorems.

Axiom 1: If a transversal intersects two parallel lines, then each pair of corresponding angles is equal. This axiom is known as a corresponding angle axiom.
When line l intersects two parallel lines m and n, then we see that each pair of corresponding angles is equal.
∴ ∠ 1 = ∠5, ∠2 = ∠6, ∠4 = ∠8 and ∠3 = ∠7
The converse of this axiom is as follows:
Axiom 2 (Converse of axiom 1): If a transversal intersects two lines such that a pair of corresponding angles are equal, then the two lines are parallel to each other.
Theorem 1: If a transversal intersects two parallel lines, then each pair of alternate angles is equal.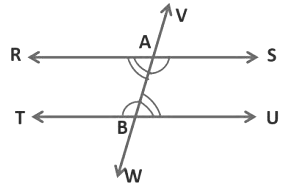
Here, line VW intersects two parallel lines RS and TU at points A and B respectively.
The two pairs of alternate interior angles are∠SAB and ∠TBA, ∠RAB and ∠ABU
To prove:
(i) ∠SAB = ∠TBA
(ii) ∠RAB = ∠ABU
We know,
∠VAR = ∠SAB (Vertically opposite angles) → Eq 1
∠VAR = ∠TBA (Corresponding angles axiom) Eq → 2
Using Eq 1 and 2 we see that,
∠VAR = ∠SAB and∠VAR = ∠TBA. Therefore, ∠SAB = ∠TBA
Similarly,
∠SAV = ∠RAB (Vertically opposite angles) Eq → 3
∠SAV = ∠ABU (Corresponding angles axiom) Eq → 4
Using Eq 3 and 4 we get,
∠SAV = ∠RAB and ∠SAV = ∠ABU. Therefore, ∠RAB = ∠ABU
So,∠SAB = ∠TBA and ∠RAB = ∠ABUTherefore, the pairs of alternate interior angles are equal.
Theorem 2 (Converse of theorem 1): If a transversal intersects two lines such that a pair of alternate interior angles are equal, then the two lines are parallel.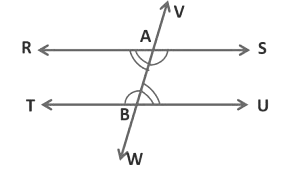
Here, line VW intersects two parallel lines RS and TU at points A and B respectively in such a way that,∠SAB = ∠TBA and ∠RAB = ∠ABU.
To prove: RS is parallel to TU
We know,
∠SAB = ∠TBA (alternate interior angles) Eq → 1
∠SAB = ∠RAV (vertically opposite angles) Eq → 2
Using Eq 1 and 2 we see that,
∠SAB = ∠TBA and ∠SAB = ∠RAV. Therefore, ∠TBA = ∠RAV.
We know that∠TBA and ∠RAV are corresponding angles.According to the converse of corresponding angles axiom, if a transversal intersects two lines such that a pair of corresponding angles are equal, then the two lines are parallel to each other.
So, RS and TU are parallel lines, that are RS || TU.
Theorem 3: If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
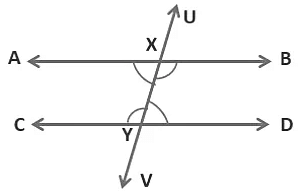
Here, line UV intersects two parallel lines AB and CD at points X and Y respectively. So, two pairs of interior angles are formed; ∠AXY and ∠CYX, ∠BXY and ∠XYD.To prove: ∠AXY + ∠CYX = 180° and ∠BXY + ∠XYD = 180°
(pair of interior angles on the same side of the transversal is supplementary)
Here, ray XY stands on line AB. Therefore, ∠AXY and ∠BXY are adjacent angles.
So, ∠AXY + ∠BXY = 180° → Eq 1
(linear pair axiom states that if a ray stands on a line, then the sum of two adjacent angles so formed is 180°)
Now, ∠BXY = ∠CYX (alternate interior angles) → Eq 2
On putting ∠BXY = ∠CYX in Eq 1 we get,
∠AXY + ∠CYX = 180°
Similarly, ray XY stands on line CD. Therefore, ∠CYX and ∠XYD are adjacent angles.
So, ∠CYX + ∠XYD = 180° (linear pair axiom) Eq → 3
But, ∠CYX = ∠BXY (alternate interior angles) Eq → 4
On putting ∠CYX = ∠BXY in Eq 1 we get,
∠BXY + ∠XYD = 180°
Therefore,
∠AXY + ∠CYX = 180°
∠BXY + ∠XYD = 180°
Theorem 4 (Converse of theorem 4): If a transversal intersects two lines, in such a way that each pair of interior angles on the same side of the transversal is supplementary, then the lines are parallel.

Here, line UV intersects two parallel lines AB and CD at points X and Y respectively in such a way that two pairs of interior angles on the same side of the transversal are ∠AXY and ∠CYX, ∠BXY and ∠XYD.
We know, ∠AXY + ∠CYX = 180°
∠BXY + ∠XYD = 180°
To prove: AB || CD
Here, ray XB stands on line UV. Therefore, ∠BXU and ∠BXY are adjacent angles.
So, ∠BXU + ∠BXY = 180° (linear pair axiom) → Eq 3
(linear pair axiom states that if a ray stands on a line, then the sum of two adjacent angles so formed is 180°)
It is given that,
∠BXY + ∠XYD = 180° → Eq 4
Using Eq 3 and 4 we get,
∠BXU + ∠BXY = ∠BXY + ∠XYD
On subtracting ∠BXY from both sides we get,
∠BXU + ∠BXY - ∠BXY = ∠BXY + ∠XYD - ∠BXY
∠BXU + ∠BXY - ∠BXY = ∠BXY - ∠BXY + ∠XYD
So, ∠BXU = ∠XYD
Now, ∠BXU and ∠XYD are corresponding angles.
According to the converse of corresponding angles axiom, if a transversal intersects two lines such that a pair of corresponding angles are equal, then the two lines are parallel to each other. So, AB || CD.
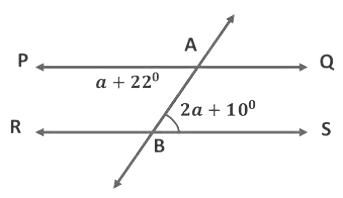
Example 1: In the figure given below, PQ ||RS, find the value of a and ∠PAB and ∠ABR.
Now, ∠PAB = ∠ABS (Alternate interior angles)
a + 220 = 2a + 10°
22° − 10° = 2a − a
a = 12°
∠PAB = a + 22°
∠PAB = 12° + 22°(∵ a = 12°)∠PAB = 34°
We know, ∠PAB = ∠ABS = 34°
Ray AB stands on line RS. Therefore, ∠ABR and ∠ABS are adjacent angles.
So, ∠ABR + ∠ABS = 18° (linear pair axiom)
∠ABR +34° = 180°(∵ ∠PAB = 34°)
∠ABR = 180° − 34°= 126°
∠ABR = 126°
Example 2: In the figure, PQ ||RS ||TU and a ∶ b = 1 : 2, find c.
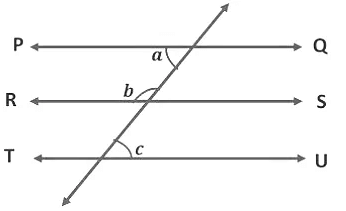
Let, a = 1x and b = 2x
Now, a and b are interior angles on the same side of the transversal.If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
Therefore, a + b = 180°
x + 2x = 180° (∵ a = 3x, b = 2x)
3x = 180°
x = 180°/3 = 60°
Now, a = x = 60°
b = 2x = 2 × 60° = 120°
a = c = 60° (Alternate interior angle)
c = 60°
Example 3: In the figure PQ || RS, ∠PQX = 35° and ∠RSX = 40°, find a.
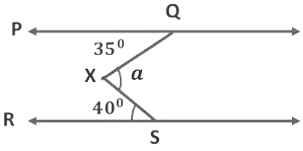
Here we draw a line m parallel to PQ through X.

Here, ∠PQX = ∠QXY = 35° (Alternate interior angle)
Again, ∠RSX = ∠YXS = 40° (Alternate interior angle)
Now, ∠QXS = ∠QXY + ∠YXS
∠QXS = 35° + 40°(∵ ∠QXY = 35° and ∠YXS = 40°)
∠QXS = 75°
∠QXS = a = 75°
Therefore, a = 75°
|
44 videos|412 docs|54 tests
|
FAQs on Lines and Angles Class 9 Notes Maths Chapter 6
| 1. What are intersecting and non-intersecting lines? |  |
| 2. What are the different pairs of angles formed when two lines intersect? |  |
| 3. How do you determine if two lines are parallel to the same line? |  |
| 4. What is the angle sum property of a triangle? |  |
| 5. What are parallel lines and transversal lines? |  |

|
Explore Courses for Class 9 exam
|

|


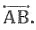
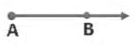







 Line m || line n.
Line m || line n.

















