Operations on Large Numbers Class 5 Notes Maths
| Table of contents |

|
| Large Numbers |

|
| Number Names & Expanded Form |

|
| Comparing & Ordering Large Numbers |

|
| Arithmetic Operations on Large Numbers |

|
| International System of Writing Numbers |

|
Large Numbers
Have you ever wondered how we count things that are really big? Think about:
- How many people live in your city?
- How many stars are in the sky?
For such huge things, we need large numbers.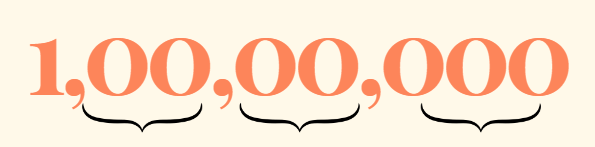 In this Chapter, you’ll learn to read, write, compare, and play with large numbers so you can measure the big things all around us.
In this Chapter, you’ll learn to read, write, compare, and play with large numbers so you can measure the big things all around us.
Indian Place Value Chart
Following is the table for the Indian Place Value System to let students understand how numbers are arranged and read.
Example: Write the numeral by separating periods of the following
1. 603274087
Ans: 60,32,74,087
Sol:
Step 1: Identify the periods(refer to the table given above):
Crore: 60
Lakh: 32
Thousand: 74
Ones: 087
Step 2: Put commas
After putting commas according to the periods we get = 60,32,74,087
2. 37007690
Ans: 3,70,07,690
Sol:
Step 1: Identify the periods(refer to the table given above):
Crore: 3
Lakh: 70
Thousand: 07
Ones: 690
Step 2: Put commas
After putting commas according to the periods we get = 3,70,07,690
Number Names & Expanded Form
1. Number Names
To write number name for any given number, we must follow the following steps
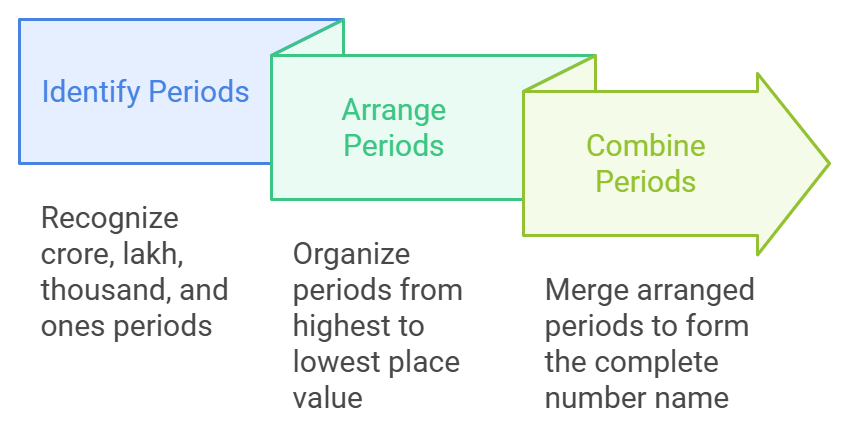
We will refer to some solved examples for better clarity of the concept
Example 1: Write number name for the following
1. 76,23,45,809
Ans: Seventy-six crore twenty-three lakh forty-five thousand eight hundred nine.
Sol:
Step 1: Break it down
Crore: 76
Lakh: 23
Thousand: 45
Ones: 809
Step 2: Arrange and combine
Seventy-six crore twenty-three lakh forty-five thousand eight hundred nine.
2. 1,05,08,406
Ans: One crore five lakh eight thousand four hundred six.
Sol:
Step 1: Break it down
Crore: 1
Lakh: 05
Thousand: 08
Ones: 406Step 2: Arrange and combine
One crore five lakh eight thousand four hundred six.
2. Expanded Form
Refer to the following example to understand the concept of expanded form
Example 2: Write 45,76,90,213 in expanded form
Sol:
Step 1: The given number is 45 crore 76 lakh 90 thousand 2 hundred thirteen.
The given number in the place value chart is as shown below.Step 2: Write the table into number name format
Thus, 45,76,90,213 = 4 ten crores + 5 crores + 7 ten lakhs + 6 lakhs+ 9 ten thousands + 0 thousands + 2 hundreds+ 1 ten + 3 onesStep 3: Mathematically we can write it as
= 4 x 100000000 + 5 x 10000000 + 7 x 1000000 + 6 x 100000 + 9 x 10000 + 0 x 1000 + 2 x 100 + 1 x 10 + 3
= 400000000 + 50000000 + 7000000 + 600000 + 90000 + 0 + 200 + 10 + 3
Comparing & Ordering Large Numbers
In this section, we will learn about the following three things

1. Comparing Large Numbers
For comparing large numbers , we have two cases:
Case 1: Unequal number of digits
The number having more digits is greater than the number having fewer digits.
Example 1: Which is greater: 8,93,10,009 or 11,00,73,640?
Sol: On counting both of the digits we found out that,
11,00,73,640 has 9 digits whereas 8,93,10,009 has 8 digits.
and 9 is greater than 8.
therefore, 11,00,73,640 > 8,93,10,009.
Case 2: Equal number of digits
Start from the left and compare the digits until they differ.
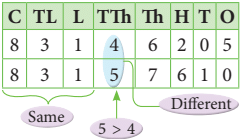
Example 2: Compare 8,31,46,205 and 8,31,57,610?
Sol: As we can see both of these numbers have same number of digits,
therefore we start comparing from the left until both of them differ.The digits differ at the ten thousands place.
5 > 4,
So, 8,31,57,610 > 8,31,46,205.
2. Ordering Large Numbers:
In this , we will arrange large numbers into ascending or descending order according to their values.
Example 3: Arrange the following numbers in descending order.
8,36,04,295 ; 40,34,51,276 ; 3,04,63,500 ; 89,72,340 ; 99,00,32,941
Sol:
Step 1: Line up the numbers by their place valuesStep 2:
There are two 9-digit numbers, two 8-digit numbers and one 7-digit number.
Comparing 9-digit numbers.
9 TC > 4 TC,
So, 99,00,32,941 > 40,34,51,276
Comparing 8-digit numbers.
8 crore > 3 crore, ∴ 8,36,04,295 > 3,04,63,500
7-digit number is the smallest.
Hence, the numbers written in descending order are:
99,00,32,941 > 40,34,51,276 > 8,36,04,295 > 3,04,63,500 > 89,72,340.
3. Formation of Smallest & Greatest Numbers
For forming smallest and the greatest numbers from a given collection of numbers , we have following cases
Case 1: Repetition of Digits is not Allowed
When repetition of numbers is not allowed,
1. Greatest Number :We place the greatest digit at the leftmost place and the other digits in descending order.
2. Smallest Number: We place the smallest at the leftmost place and the other digits in ascending order.
Example 4: Write the smallest and the greatest 7-digit number by using the digits 0, 2, 4, 6, 5, 8 and 9 only once.
Sol:
1. Smallest Digit:
For writing the smallest number, we place the smallest digit at the leftmost place and write the other digits in ascending order.
Here, 0 is the smallest digit but we cannot begin a number with 0.
So, we write the next higher digit which is 2 in this case.
So, the smallest 7-digit number is 2045689
2. Greatest Digit:
For writing the Greatest Number, We place the greatest digit at the leftmost place and the other digits in descending order.
Here, 9 is the greatest digit
So, the greatest 7-digit number is 9865420
Case 2: Repetition of Digits is Allowed
Example 5: Write the smallest and the greatest 7-digit number by using the digits 0, 1, 4, 6, 5, 8 and 9, where repetition is allowed.
Sol: Greatest Number: 9999999
Smallest number : 1000000
Arithmetic Operations on Large Numbers
The arithmetic operations on the large numbers are given below- Addition of Large numbers
- Subtraction of Large Numbers

1. Addition
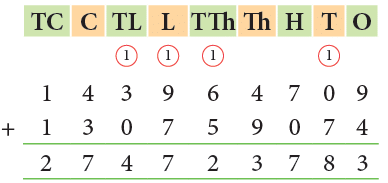
In case of addition of large numbers, we have to add the numbers of same place values.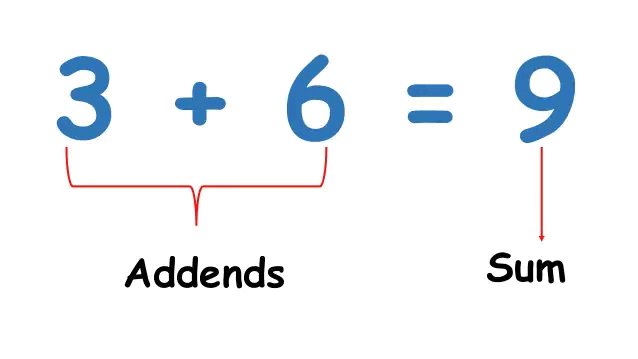 Example: The statistics on the Internet suggest that the estimated population of Russia and Mexico is 14,39,64,709 and 13,07,59,074, respectively. If the population of the USA is 32,67,66,748, find out whether the population of Russia and Mexico taken together is more than that of the USA or not.
Example: The statistics on the Internet suggest that the estimated population of Russia and Mexico is 14,39,64,709 and 13,07,59,074, respectively. If the population of the USA is 32,67,66,748, find out whether the population of Russia and Mexico taken together is more than that of the USA or not.
Sol:
- The population of Russia and Mexico is 27,47,23,783
- Population of USA = 32,67,66,748
- Since, 3 ten crores > 2 ten crores, the population of the USA is more than the population of Russia and Mexico taken together.
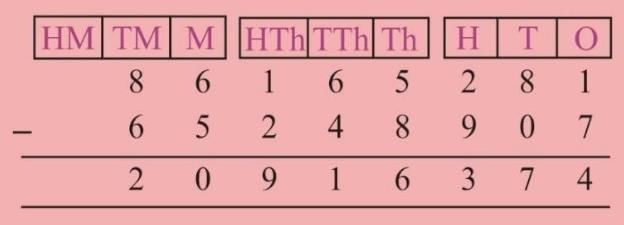
2. Subtraction
In case of subtraction of large numbers, we have to subtract the numbers of same place values.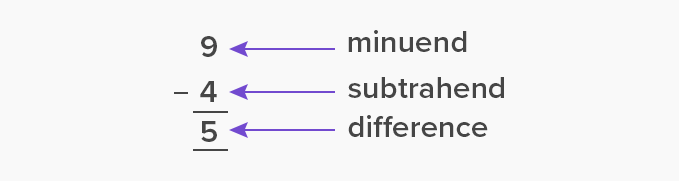
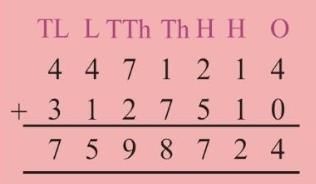
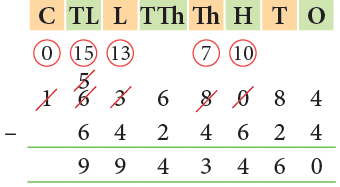
Example : The population of Greater Mumbai and Chennai as per the 2011 census was 1,63,68,084 and 64,24,624, respectively. How much more is Greater Mumbai’s population as compared to Chennai?
Sol:
- The population of Greater Mumbai = 1,63,68,084
- Population of Chennai = 64,24,624
- Population difference = 1,63,68,084 – 64,24,624 = 99,43,460
- Thus, the population of Greater Mumbai is 99,43,460 more than that of Chennai.
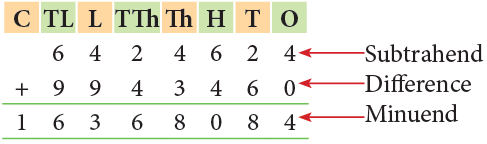
- You can check subtraction by adding the subtrahend to the difference. If the sum is equal to the minuend, then the subtraction has been carried out correctly.
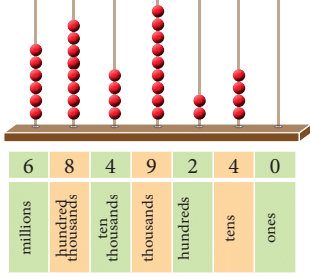
International System of Writing Numbers
In International system, the number 10 lakh is called a million and furthermore every bigger calculations is in millions.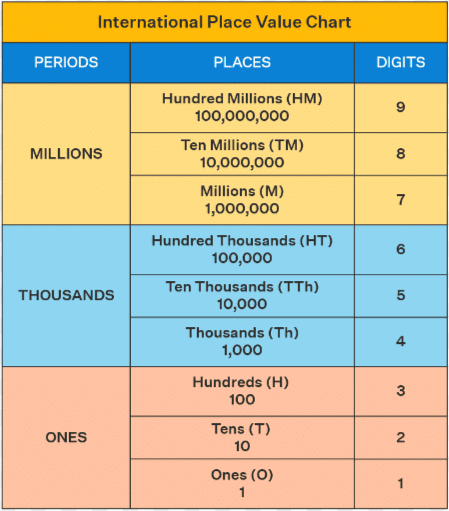
The chart can be extended to its left to include more than 9 places. The period just to the left of the millions period is called the billions period. Then, we have the trillions period and so on.
On comparing the two systems of numerations, we can observe the following relationships.
- 10 lakh = 1 million
- 1 crore = 100 lakh = 10 million
- 10 crore = 100 million
- 100 crore = 1,000 million = 1 billion
- 1000 crore = 10,000 million = 10 billion
Did You Know
- The Indian system, starting from the right after the first period of 3 digits all other periods are of 2 digits.
- In the International system, each period consists of three digits.
- We place comma or leave space after every 3 digits.
Example 1: Write in numerals:
(a) 8 million
(b) Eighty-five million three hundred five thousand nine hundred
Sol:
(a) 8 million = 8,000,000
(b) Step by step breakdown of the numbers1. Eighty-five million = 85,000,000
2. Three hundred five thousand = 305,000
3. Nine hundred = 900
On adding we get, 85,305,900
Example 2: Number names in international system:
1. 23,450,789
Sol: Number Name for the same is given below
Number Name: Twenty-three million four hundred fifty thousand seven hundred eighty-nine
2. 105,067,092
Sol: Number Name for the same is given below
Number Name: One hundred five million sixty-seven thousand ninety-two
Example 3: Write ‘sixty-nine crore four lakh forty-one thousand six hundred twenty-seven’ in the International system.
Sol: The numeral in Indian system is 69 04 41 627.
On writing it in International system, we get,
Numeral : 690,441,627
Number Name : Six hundred ninety million four hundred forty-one thousand six hundred twenty-seven.
|
56 videos|187 docs|40 tests
|
FAQs on Operations on Large Numbers Class 5 Notes Maths
| 1. What are large numbers and how do we write them in number names? |  |
| 2. How do you expand a large number into its expanded form? |  |
| 3. How can we compare and order large numbers effectively? |  |
| 4. What are the basic arithmetic operations we can perform on large numbers? |  |
| 5. What is the International System of Writing Numbers? |  |