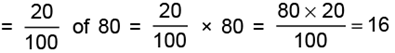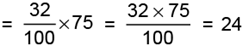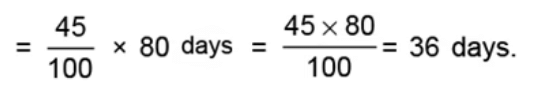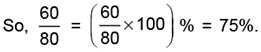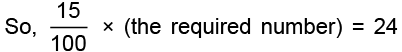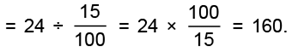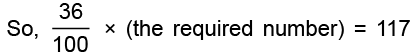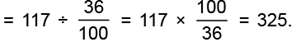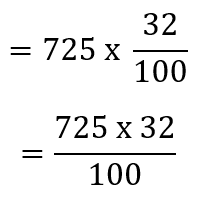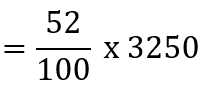Percentages Class 5 Notes Maths
| Table of contents |

|
| Introduction |

|
| To Convert Fractions, Decimals, and Percentages from One Form to Another |

|
| Money and Metric Measures as Percentages |

|
| Finding the Percentage of a Number |

|
| Word Problems |

|
- Did you know that 'per cent' means 'per hundred'?
- Imagine splitting anything into 100 equal parts—a chocolate bar, a pizza, or a test score.
In this Chapter, we’ll learn how percentages make comparing things easier. Get ready to unlock the power of 100.
Introduction
- Per means out of and cent means 1 hundred. Therefore, per cent means out of 1 hundred.
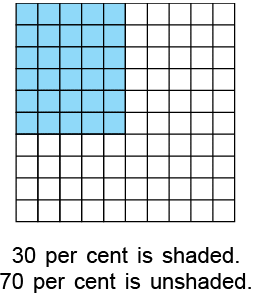
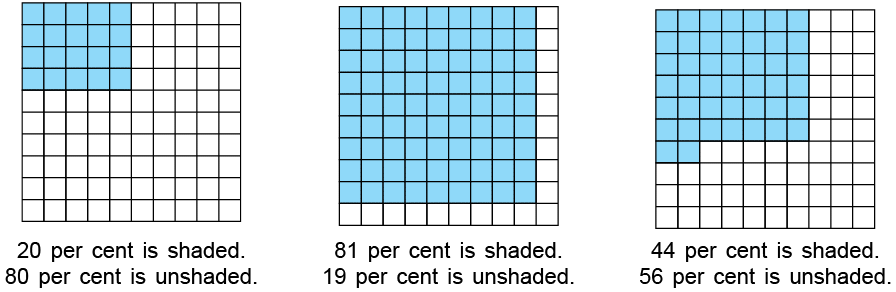
- In the figure, a square is divided into 100 equal parts. Out of the 100 small squares, 30 squares are shaded.
- The shaded part comprises 30 out of 100 or 30 per cent of the whole.
- The unshaded part comprises 70 per cent of the whole.
- The symbol of per cent is %.
- So, 7% means 7 out of 1 hundred = 7 / 100.
20% means 20 out of 1 hundred = 20 / 100.
80% means, 80 out of 1 hundred = 80 / 100. - We note that a fraction with 100 as the denominator can be considered as a per cent.
For example, 15 / 100 means 15% and 60 / 100 means, 60%. - In an examination, Priya secured 72% marks. What does it mean?
It means she obtained 72 marks out of 100 marks.
To Convert Fractions, Decimals, and Percentages from One Form to Another
(i) To Convert a Fraction into a Percentage
Rule: To convert a fraction into a percentage, multiply by 100.
Example Calculations:
- 46/100 = (46 × 100)% = 46%
- 2/5 = (2 × 100)% = 40%
- 13/15 = (15 × 100)% = 86 2/3%
(ii) To Convert a Percentage into a Fraction
Rule: To convert a percentage into a fraction, divide by 100.
Example Calculations:
- 32% = 32/100 = 16/50 = 8/25
- 158% = 158/100 = 79/50 = 129/100
- 53/8% = 53/8 × 1/100 = 53/800
- 2.4% = 2.4 × 1/100 = 24/100 = 125/10
(iii) To Convert a Decimal into a Percentage
Rule: To convert a decimal into a percentage, multiply by 100 or shift the decimal point two places to the right.
Example Calculations:
- 0.37 = (0.37 × 100)% = 37%
- 18.54 = (18.54 × 100)% = 1854%
(iv) To Convert a Percentage into a Decimal
Rule: To convert a percentage into a decimal, divide by 100 or shift the decimal point two places to the left.
Example Calculations:
- 74% = 74/100 = 0.74
- 1842% = 1842/100 = 18.42
Money and Metric Measures as Percentages
1. We know that 100 paise = 1 rupee.
1 paisa = 1 / 100 of a rupee.
1 paisa = 1% of a rupee.
Similarly, 2 paise = 2% of a rupee.
10 paise = 10% of a rupee.
75 paise = 75% of a rupee.
2. We know that 100 cm = 1 metre
So, 1 cm = 1 / 100 of a metre.
1 cm = 1% of a metre.
2 cm = 2% of a metre.
20 cm = 20% of a metre.
3. We know that 1,000 g = 1 kg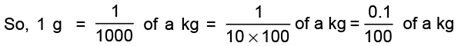
1 g = 0.1% of a kg.
2 g = 0.2% of a kg.
15 g = 1.5% of a kg
100 g = 10% of a kg.
500 g = 50% of a kg.
4. We know that 1,000 ml = 1l
1 ml = 0.1% of a l.
3 ml = 0.3% of a l.
10 ml = 1% of a l.
250 ml = 25% of a l.
Finding the Percentage of a Number
The following examples will help you to understand the required procedure.
Example 1: Find:
(a) 20% of 80
(b) 32% of 75
(c) 45% of 80 days
(a) 20% of 80
Hence, 20% of 80 = 16.
(b) 32% of 75
Hence, 32% of 75 = 24
(c) 45% of 80 days
Hence, 45% of 80 days = 36 days.
Example 2: What per cent of 80 is 60?
60 out of 80 is equivalent to the fraction 60 / 80.
Hence, 75% of 80 is 60.
To Find the Number Whose Percentage is Given
Example 3: Find the number whose:
(a) 15% is 24
(b) 36% is 117
(a) We have, 15% of the required number = 24
Thus, the required number
Hence, 160 is the required number whose 15% is 24.
(b) We have 36% of the required number = 117
Thus, the required number
Hence, 325 is the required number whose 36% is 117.
Word Problems
Example 4: In a school, there are 725 students. Out of these, 32 are girls. How many girls are there? Also, find the number of boys in the school.
Sol:
Total number of students = 725
Number of girls = 32% of 725
= 232
Now, the number of boys can be calculated as by subtracting the number of girls from the total number of students.
Number of boys in the school = 725 - 232 = 493
Example 5: The population of a village is 3,250 out of them 52% are males. Find the number of males in the village. Also, find the number of females in the village.
Sol:
We know that 52% of the population is males. Let us find out the number.
Total population = 3,250
Males in the population = 52% of 3250
= 1690
Therefore, there are 1,690 males in the village.
To find out the number of females in the village, we simply subtract the number of males from the total population.
Number of females = 3250 - 1690 = 1560
|
56 videos|187 docs|40 tests
|
FAQs on Percentages Class 5 Notes Maths
| 1. How do I convert a percentage into a fraction? |  |
| 2. What is the method to convert a fraction into a percentage? |  |
| 3. How can I find the percentage of a number? |  |
| 4. Can you explain how to convert a decimal into a percentage? |  |
| 5. What are some common applications of percentages in money and metric measures? |  |