Perimeter and Area Class 5 Notes Maths
Perimeter
Aditya jogs four times around a rectangular park every day. How much distance does he jog every day?
Mrs Saini is stitching a lace around the square handkerchief for her granddaughter. How much lace does she need?
All these types of questions referring to the distance around a plane figure are answered by ‘‘Perimeter’’.
What is Perimeter?
The word perimeter is derived from two Greek words peri meaning around and metron meaning measure.
Thus, we measure the perimeter of a plane figure by adding the lengths of its sides.
Perimeter is the distance around a plane figure or the length of the boundary of a plane figure.
Observe the following examples.
• If the rectangular park is of 150 m length and 80 m width, then
• Distance jogged by Aditya everyday = 4 × perimeter of the park
= 4 × (150 + 80 + 150 + 80) m
= 4 × (460) = 1840 m
• If each side of the square handkerchief is 10 cm, then lace required by Mrs Saini = Perimeter of the handkerchief
= 10 + 10 + 10 + 10 cm = 40 cm
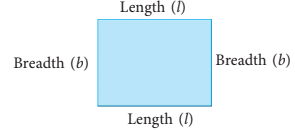
Perimeter of a Rectangle
A rectangle is a plane figure whose opposite sides (facing each other) are of equal lengths.
So, we have two equal lengths and two equal breadths.
Perimeter of a rectangle = length + breadth + length + breadth
= length + length + breadth + breadth
= 2 × length + 2 × breadth
= 2 × (length + breadth) = 2 × (l + b)
Perimeter of rectangle = 2 × (length + breadth)
Example 1: Find the perimeter of a bedsheet whose length is 8 m and breadth is 5 m.

Perimeter of the bedsheet
= 2 × (length + breadth)
= 2 × (8 m + 5 m) = 2 × 13 m = 26 m
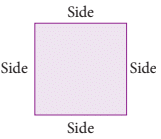
Perimeter of a Square
A square is a plane figure whose all four sides are of equal lengths.
Perimeter of a square = side + side + side + side
= 4 × side
Perimeter of a square = 4 × length of one side
Example 2: Find the perimeter of a square photo frame of a side 40 cm.
Perimeter of the photo-frame
= 4 × side
= 4 × 40 cm
= 160 cm
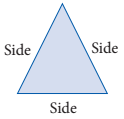
Perimeter of an Equilateral Triangle
An equilateral triangle is a triangle whose all three sides are equal.
Perimeter of an equilateral triangle = side + side + side = 3 × side.
Perimeter of an equilateral triangle = 3 × length of one side
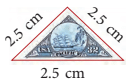
Example 3: A stamp is in the shape of an equilateral triangle. Its each side measures 2.5 cm. What is the length of the boundary of the stamp?
Length of the boundary of the stamp = 3 × side
= 3 × 2.5 cm = 7.5 cm
Example 4: Mr Kapoor wants to put a wooden border around a painting. If the length of the painting is 40 cm and its breadth is 25 cm, what will be the cost of putting the border at Rs.40 per cm?
Length of the painting = 40 cm
Breadth of the painting = 25 cm
Perimeter of the painting = 2 (length + breadth)
= 2 × (40 cm + 25 cm) = 2 × 65 cm = 130 cm
Now, cost of putting 1 cm border = Rs.40.
Thus, cost of the border for the whole painting = Rs.130 × 40 = Rs.5200
Example 5: The perimeter of a rectangular field is 42 m and its length is 10 m. Find its breadth.

Perimeter = 2 × (length + breadth)
Therefore, length + breadth = Perimeter ÷ 2
10 m + breadth = 42 m ÷ 2 = 21 m
Breadth = 21 m – 10 m = 11 m
Example 6: What is the length of the side of a square park whose perimeter is 80 m?
Perimeter of a square = 4 × side
∴ Side = Perimeter ÷ 4
Thus, length of a side of the square park = 80 m ÷ 4 = 20 m
Area
You have been introduced to the concept of area in Class IV. Let us revise. How many marble tiles can fit on the floor or wall? How much paint is needed for the wall? All these questions are referring to the surface within the boundary and are answered by Area.
What is Area?
Area of a shape is the amount of space it covers.
It refers to the flat surface taken by a plane figure. The coloured part of each of the shapes shows the amount of space covered by each of them on this sheet of paper, i.e., it shows their area. Which shape has greater area? To answer this question we need to know as to which shape covers more surfaces on paper. Obviously, shape C.
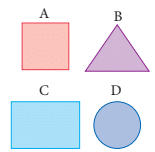
Area is found by calculating how many square units are needed to exactly cover the given shape.
Units of Measurement of Area
The units used to measure area are based on the units of length, i.e., mm, cm, m and km.
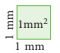 This is an area equal to 1 square millimetre (mm2).
This is an area equal to 1 square millimetre (mm2).
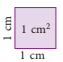 This is an area equal to 1 square centimetre (cm2).
This is an area equal to 1 square centimetre (cm2).
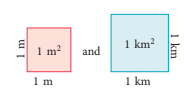 represent other units of measuring area such as 1 square metre (m2) and 1 square kilometre (km2).
represent other units of measuring area such as 1 square metre (m2) and 1 square kilometre (km2).
The unit used for measuring the area depends on the size of the area being measured.
For example, the areas of the following shapes are usually measured as under:

Finding Area Using Square Grid
The area of the shaded shapes can be estimated by counting the number of unit squares they cover. Give your answer in square units. Here, we have some half squares also. Count 2 half squares as 1 unit2.
1.
Full squares = 22
Half = 6
More than half squares = 3
∴ Area of figure = 22 + 6 × 1/2 + 2 = 27 sq units.
2. 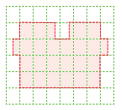
Full squares = 22
Half = 4
∴ Area of figure = 22 + 4 × 1/2 = 24 sq units.
(The area of three more than half squares is almost equal to the area of 2 full squares.)
Area of a Rectangle
Here are three rectangles, covered with small squares. Each small square stands for 1 square centimetre, i.e., each small square is 1 cm on each side.

Count the number of small squares that cover each rectangle. This will give you the area of the rectangle in square centimetres. Also, write the length and breadth of each rectangle in centimetres. What do you observe?

From the above examples, you can see that there is a quick way to find the area in each case without having to count the smaller squares. Since 4 × 3 = 12; 5 × 4 = 20 and 7 × 1 = 7, we can say that the area of each of the rectangles can be found out by multiplying the measures of length and breadth of the rectangle.

Conclusion
Area (A) of a rectangle of length l and breadth b is l × b.
i.e., Area of a rectangle = length × breadth
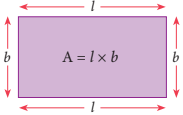
Let us see more examples.

Area of a Square
A square is a rectangle whose length and breadth are equal, so its area = length × length.
Therefore, Area of a square = side × side = side2.
Example 7: (a) Find the length of a rectangle if its area = 120 cm2 and its breadth = 10 cm
(b) Find the breadth of a rectangle if its area = 91 cm2 and its length = 13 cm.
(a) Area = 120 cm2, Breadth = 10 cm
∴ Length = Area ÷ Breadth
= 120 cm2 ÷ 10 cm = 12 cm.
(b) Area = 91 cm2, Length = 13 cm
∴ Breadth = Area ÷ Length
= 91 cm2 ÷ 13 cm = 7 cm.
Example 8: The perimeter of a square is 24 cm. Find its area.
To find the area, we need the side of the square.
Side of the square = Perimeter ÷ 4
= 24 cm ÷ 4 = 6 cm
∴ Area = side × side = 6 cm × 6 cm = 36 cm2.
|
56 videos|187 docs|40 tests
|
FAQs on Perimeter and Area Class 5 Notes Maths
| 1. What is the formula to calculate the perimeter of a shape? |  |
| 2. How can I find the area of a shape using a square grid? |  |
| 3. What is the difference between perimeter and area? |  |
| 4. Can the perimeter and area of a shape be the same? |  |
| 5. Are there any shortcuts or tricks to calculate the perimeter and area of shapes? |  |