Play With Patterns Chapter Notes | Mathematics for Class 4: NCERT PDF Download
| Table of contents |

|
| Introduction |

|
| Patterns |

|
| Magic patterns |

|
| Magic triangles |

|
| Number towers |

|
| The same sum rule |

|
| Patterns with addition |

|
| Secret message |

|
| Upside down |

|
| Floor patterns |

|
Introduction
Today, we're embarking on an exciting journey into the colorful world of patterns. Just like the vibrant designs on your favorite shirts or the rhythmic sequences in your favorite songs, patterns are all around us, waiting to be discovered and explored. In this math adventure, we'll learn how to recognize, create, and extend patterns, unlocking the secrets behind their mesmerizing repetitions. From simple shapes to complex sequences, patterns help us make sense of the world and sharpen our problem-solving skills. So, get ready to unleash your creativity, sharpen your observation skills, and dive into the enchanting realm of playing with patterns!"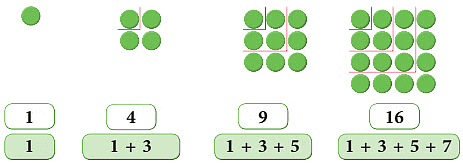
Patterns
Patterns are repeating sequences found in numbers, shapes, colors, and actions. Students recognize, create, and extend patterns, developing critical thinking and problem-solving skills. By identifying underlying rules, they apply pattern recognition to real-world scenarios, laying the foundation for advanced mathematical concepts.
Magic patterns
Magic patterns, like magic squares or triangles, are arrangements of numbers where the sum of each row, column, and diagonal equals the same value. They're fascinating puzzles that challenge us to arrange numbers in a way that creates this magical sum. These patterns offer insights into math concepts like symmetry and number theory, making them both engaging and educational.
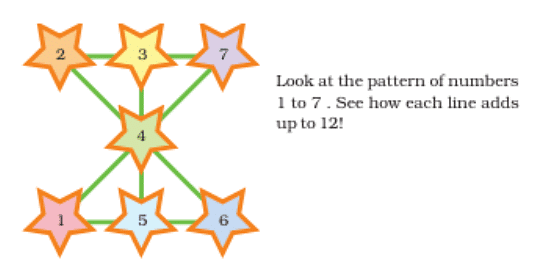
as 2+4+6=12 , 3+4+5=12 , 7+4+1 =12
Magic triangles
Magic triangles are similar to magic squares but are arranged in a triangular shape. In a magic triangle, the numbers are arranged in rows so that the sum of each row, as well as the sum of the numbers along the diagonal, equals the same value. Like magic squares, magic triangles provide an engaging challenge for puzzle enthusiasts and offer insights into mathematical concepts such as symmetry and number theory.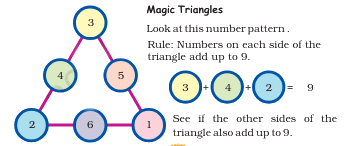
as you can see 3+4+2=9 , 2+6+1=9 , 3+5+1 = 9
Number towers
Magic towers are three-dimensional puzzles where each level and diagonal plane has the same sum of numbers. Each cube contains a unique number, and arranging them to create this sum presents a challenging puzzle. They offer an intriguing exploration of mathematical concepts in three dimensions, such as symmetry and spatial reasoning.
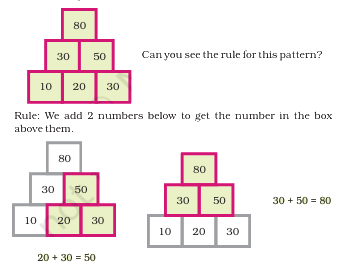
The same sum rule
The "same sum rule" in mathematics states that in arrangements like magic squares, triangles, or towers, the sum of numbers in each row, column, and diagonal remains constant. This principle provides structure and challenges us to arrange numbers accordingly. It's fundamental in various puzzles and mathematical scenarios where maintaining a consistent sum is key.
as you can see 11+16 =27 12+15=27 13+14 = 27
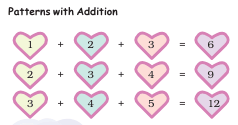
Patterns with addition
Patterns with addition involve sequences where each term is obtained by adding a fixed number to the previous term. They're fundamental in arithmetic, aiding in identifying, extending, and predicting future terms.
Secret message
Secret messages hidden within patterns involve encoding information using a predetermined pattern. For example, assigning each letter of the alphabet a numerical value and then using addition or another operation to encode a message within a sequence of numbers. Decrypting the message requires knowledge of the pattern used for encoding. These methods can be fun and challenging ways to send hidden messages or solve puzzles.

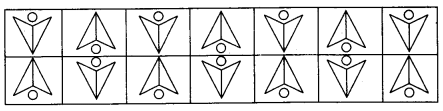
Upside down
"Upside down" typically refers to a situation where something is inverted or reversed from its usual orientation. For example, flipping a shape or text vertically so that what was previously at the top is now at the bottom. This concept can also apply to numbers, patterns, or any other visual or symbolic representation. It's often used in puzzles or games to add complexity or challenge.
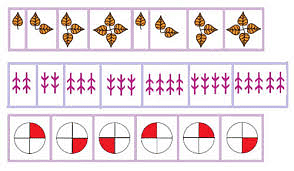
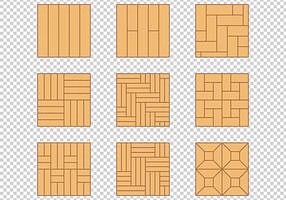
Floor patterns
A floor pattern is a design created by arranging materials like tiles or wood on the floor. These patterns vary from simple to complex, adding visual appeal and functionality to a space. They're commonly used in interior design to enhance aesthetics and define different areas within a room.
|
26 videos|142 docs|34 tests
|
FAQs on Play With Patterns Chapter Notes - Mathematics for Class 4: NCERT
| 1. What are some examples of patterns discussed in the chapter "Play With Patterns"? |  |
| 2. How can magic triangles be used to create patterns in the chapter? |  |
| 3. What is the significance of the same sum rule in the context of patterns? |  |
| 4. How can patterns with addition be used to convey a secret message? |  |
| 5. How can floor patterns be created and used in the context of patterns? |  |




















