Quadrilaterals Class 9 Notes Maths Chapter 8
| Table of contents |

|
| What are Quadrilaterals? |

|
| Properties of a Parallelogram |

|
| The Mid-point Theorem |

|
| Some Solved Examples: |

|
What are Quadrilaterals?
Quadrilaterals are shapes with four sides.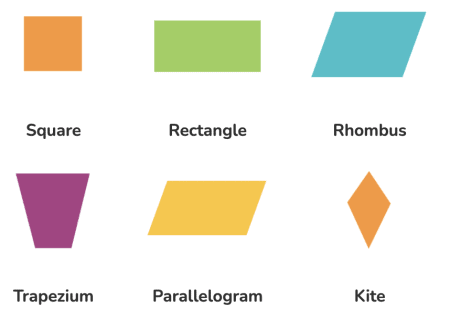 QuadrilateralsImagine the following examples:
QuadrilateralsImagine the following examples:
- Square: All four sides are equal, and all angles are right angles.
- Rectangle: Opposite sides are equal, and all angles are right angles.
- Parallelogram: Opposite sides are parallel and equal in length.
- Rhombus: All four sides are equal, but angles are not necessarily right angles.
- Examples of Quadrilaterals in Daily Life: Windows, Blackboard, Study table top, Computer screens, Mobile phone screens, Pages in a book
Definition
A quadrilateral is a closed, two-dimensional figure formed by four line segments. For instance, in quadrilateral , the line segments are , , , and .
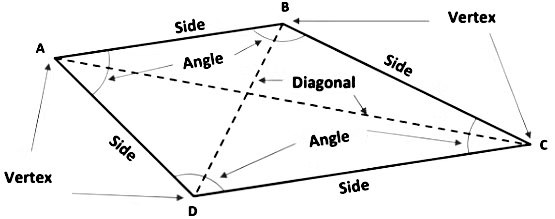
The term "quadrilateral" comes from Latin, where "quad" means "four" and "lateral" means "side."
- Sides: Four segments (e.g., , , , )
- Angles: Four angles (e.g., , , , )
- Vertices: Four points (e.g., , , , )
- Diagonals: Two segments that connect opposite vertices (e.g., and )
Properties of a Parallelogram
In geometry, a quadrilateral is a four-sided polygon with four angles and four vertices. A specific type of quadrilateral is a parallelogram, characterized by having both pairs of opposite sides parallel. Let's explore some properties of parallelograms.
Theorem 1: A diagonal of a parallelogram divides it into two congruent triangles.
Proof: Consider parallelogram ABCD with diagonal AC. Diagonal AC divides the parallelogram into triangles ∆ABC and ∆CDA. By the alternate interior angles, we have ∠BCA = ∠DAC and ∠BAC = ∠DCA. Also, AC = AC (common side).
Therefore, by the ASA rule, ∆ABC ≅ ∆CDA, and the diagonal AC divide the parallelogram into congruent triangles.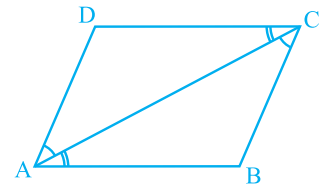
Example: In the figure, quadrilateral ABCD is a rectangle in which BD is diagonal. Show that ∆ ABD ≅ ∆ CDB.
Given: ABCD is a rectangle in which BD is diagonal.
To prove: ∆ ABD ≅ ∆ CDB.
Proof: Quadrilateral ABCD is a rectangle. Therefore, ABCD is also a parallelogram.
Since a diagonal of a parallelogram divides it into two congruent triangles.
Hence, ∆ ABD ≅ ∆ CDB.
Theorem 2: In a parallelogram, opposite sides are equal.
Proof: Measure the opposite sides AB and DC of parallelogram ABCD. You will find AB = DC. 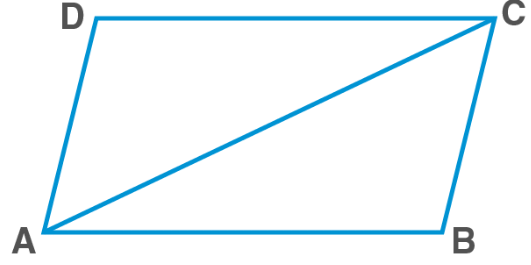
In ΔABC and ΔCDA
AC=AC [Common/transversal]
∠BCA=∠DAC [alternate angles]
∠BAC=∠DCA [alternate angles]
ΔABC≅ΔCDA [ASA rule]
Hence, AB=DC and AD=BC [ C.P.C.T.C]
Theorem 3: If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.

Given: ABCD is a parallelogram.
To prove: AB = CD and AD = CB.
Construction: Join BD.
Proof:
Since ABCD is a parallelogram. Therefore, AB ∥ DC and BC ∥ AD.
Now, AB ∥ DC and transversal BD intersects them at B and D respectively.
∴ ∠ ABD = ∠ CDB .................. (I) [Alternate interior angles]
Again, BC ∥ AD and transversal BD intersects them at B and D respectively.
∴ ∠ ADB = ∠ DBC .................. (II) [Alternate interior angles]
Now, in ∆ ABD and ∆ BDC, we have
∠ ABD = ∠ CDB [From (I)]
BD = DB [Common side]
∠ ADB = ∠ DBC [From (II)]
Therefore, ∆ ABD ≅ ∆ CDB (By ASA-criterion of congruence)
By using corresponding parts of congruent triangles
⇒ AB = CD and AD = CB.
Theorem 4: In a parallelogram, opposite angles are equal.
Proof: Measure the angles of a parallelogram; you will find that each pair of opposite angles is equal.
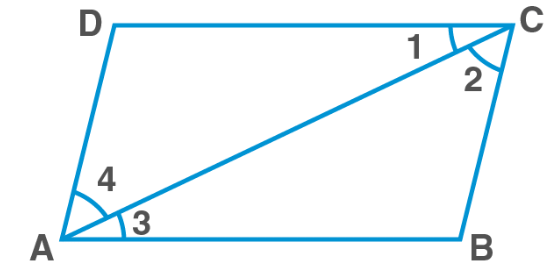
In parallelogram ABCD
AB‖CD; and AC is the transversal
Hence, ∠1=∠3….(1) (alternate interior angles)
BC‖DA; and AC is the transversal
Hence, ∠2=∠4….(2) (alternate interior angles)
Adding (1) and (2)
∠1+∠2=∠3+∠4
∠BAD=∠BCD
Similarly,
∠ADC=∠ABC
Theorem 5: If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
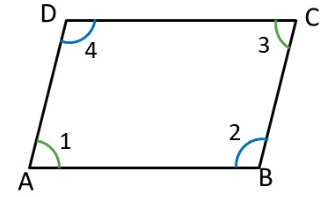
Given: In the quadrilateral, the opposite angles are equal. Let the quadrilateral be , where and .
Verification of Parallel Sides:
- Since (sum of angles in a quadrilateral equals , and opposite pairs add up), the adjacent angles are supplementary.
- This implies that and due to the converse of the consecutive angles property.
Conclusion: If both pairs of opposite sides of a quadrilateral are parallel, it is a parallelogram.
Theorem 6: The diagonals of a parallelogram bisect each other.
Proof: Draw diagonals AC and BD of parallelogram ABCD. Measure the lengths of OA, OB, OC, and OD. You will observe that OA = OC and OB = OD, or O is the midpoint of both diagonals. 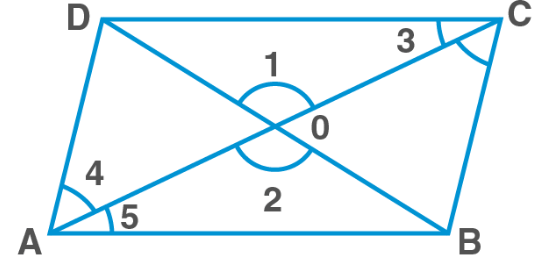
In ΔAOB and ΔCOD,
∠3=∠5 [alternate interior angles]
∠1=∠2 [vertically opposite angles]
AB=CD [opp. Sides of parallelogram]
ΔAOB≅ΔCOD [AAS rule]
OB=OD and OA=OC [C.P.C.T]
Hence, proved
Conversely,
If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
Theorem 7: If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
Example 1: Show that each angle of a rectangle is a right angle.
Solution: Consider rectangle ABCD with ∠A = 90°. By proving that ∠B = ∠C = ∠D = 90°, it establishes that each angle of a rectangle is a right angle.
Example 2: Prove that the diagonals of a rhombus bisect each other at right angles.
Solution: Consider rhombus ABCD. Let AC and BD be the diagonals, intersecting at point E. In triangles ABE and CDE, we observe that AE = CE (since ABCD is a rhombus).
Similarly, BE = DE (opposite sides of a rhombus are equal). Thus, triangles ABE and CDE are congruent by the Side-Side-Side congruence criterion. Therefore, ∠AEB = ∠CED. Now, ∠AEB + ∠CED = 180° (linear pair on straight line AECD). So, each angle measures 90°.
Hence, the diagonals AC and BD bisect each other at right angles.
The Mid-point Theorem
In geometry, the Mid-point Theorem relates to the midpoints of the sides of a triangle. The theorem establishes a relationship between the line segment joining the midpoints of two sides of a triangle and the third side.
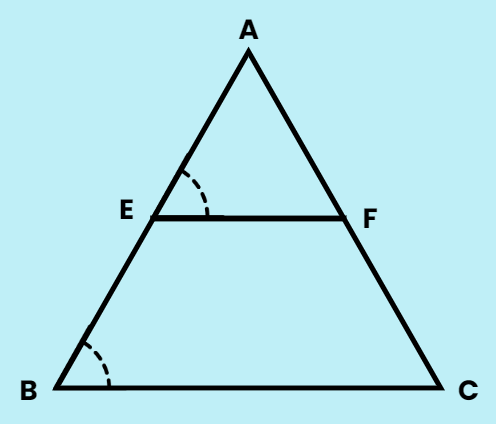
The Midpoint Theorem of a triangle states that if you connect the midpoints of two sides of a triangle with a line segment, that line segment will be parallel to the third side of the triangle, and its length will be half the length of the third side.
Let's explore this theorem and its converse.
Theorem 8: The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
Activity Observation:
- Draw a triangle and mark mid-points E and F of two sides.
- Join E and F to form line segment EF.
- Measure EF and BC. You will observe that EF = 1/2 BC.
- Measure ∠AEF and ∠ABC. You will find that ∠AEF = ∠ABC.
- Therefore, EF is parallel to BC.
Proof: Consider triangle ABC with midpoints E and F of sides AB and AC, respectively. Draw CD parallel to BA. By the ASA rule, ∆AEF ≅ ∆CDF. This implies EF = DF and BE = AE = DC. Hence, BCDE is a parallelogram, leading to EF || BC.
Theorem 9: The line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side.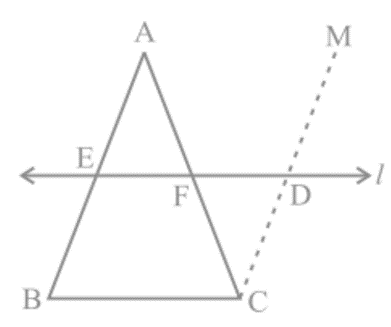
Proof: E is the mid-point of AB, and line l is parallel to BC with CM || BA. Prove AF = CF using the congruence of ∆AEF and ∆CDF.
Conclusion:
- The Mid-point Theorem and its converse provide a useful geometric relationship involving midpoints and parallel lines in triangles.
- These theorems are valuable tools for proving various properties and relationships within triangles.
Some Solved Examples:
Q.1. If the diagonals of a parallelogram are equal, then show that it is a rectangle.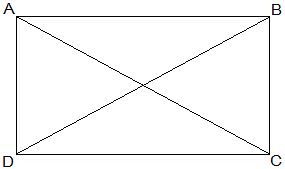
Solution: Given that, AC = BD
To show that ABCD is a rectangle if the diagonals of a parallelogram are equal
To show ABCD is a rectangle, we have to prove that one of its interior angles is right-angled.
Proof,
In ΔABC and ΔBAD,
AB = BA (Common)
BC = AD (Opposite sides of a parallelogram are equal)
AC = BD (Given)
Therefore, ΔABC ≅ ΔBAD [SSS congruency]
∠A = ∠B [Corresponding parts of Congruent Triangles]
also, ∠A+∠B = 180° (Sum of the angles on the same side of the transversal)
⇒ 2∠A = 180°
⇒ ∠A = 90° = ∠B
Therefore, ABCD is a rectangle.
Hence Proved.
Q.2. Show that the diagonals of a square are equal and bisect each other at right angles.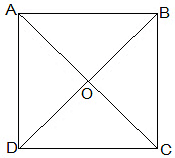
Solution: Let ABCD be a square and its diagonals AC and BD intersect each other at O.
To show that, AC = BD
AO = OC and ∠AOB = 90°
Proof,
In ΔABC and ΔBAD, AB = BA (Common)
∠ABC = ∠BAD = 90°
BC = AD (Given)
ΔABC ≅ ΔBAD [SAS congruency]
Thus, AC = BD [CPCT] diagonals are equal.
Now, In ΔAOB and ΔCOD, ∠BAO = ∠DCO (Alternate interior angles)
∠AOB = ∠COD (Vertically opposite)
AB = CD (Given)
ΔAOB ≅ ΔCOD [AAS congruency]
Thus, AO = CO [CPCT].
Diagonal bisect each other.
Now, In ΔAOB and ΔCOB,
OB = OB (Given)
AO = CO (diagonals are bisected)
AB = CB (Sides of the square)
ΔAOB ≅ ΔCOB [SSS congruency]
also, ∠AOB = ∠COB
∠AOB+∠COB = 180° (Linear pair)
Thus, ∠AOB = ∠COB = 90°
Diagonals bisect each other at right angles
Q.3. ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
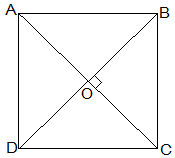
Solution:
Given that, ABCD is a rhombus.
AC and BD are its diagonals.
Proof,
AD = CD (Sides of a rhombus)
∠DAC = ∠DCA (Angles opposite of equal sides of a triangle are equal.)
also, AB || CD
⇒∠DAC = ∠BCA (Alternate interior angles)
⇒∠DCA = ∠BCA
AC bisects ∠C.
Similarly, We can prove that diagonal AC bisects ∠A.
Following the same method,
We can prove that the diagonal BD bisects ∠B and ∠D.
|
40 videos|470 docs|56 tests
|
FAQs on Quadrilaterals Class 9 Notes Maths Chapter 8
| 1. What are the properties of a parallelogram? |  |
| 2. How can the mid-point theorem be applied to a parallelogram? |  |
| 3. How can the properties of a parallelogram be used to find missing angles or sides? |  |
| 4. How do the properties of a parallelogram differ from those of a rectangle or a rhombus? |  |
| 5. Can a parallelogram have right angles? |  |





















