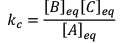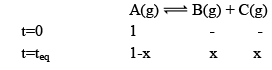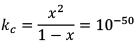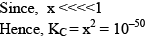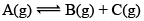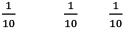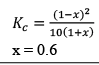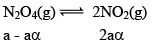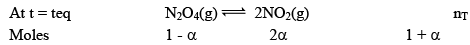Chemical Equilibrium, Law of Mass Action & Applications | Physical Chemistry PDF Download
Chemical Equilibrium
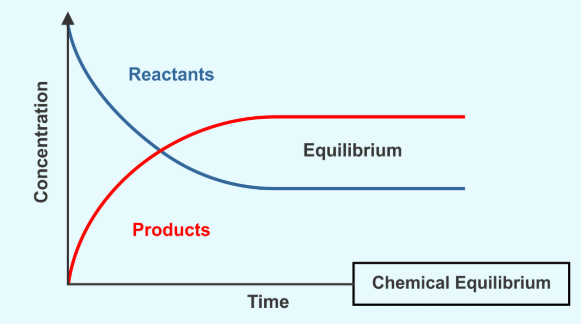
In a chemical reaction, chemical equilibrium is the state in which both reactants and products are present in concentrations which have no further tendency to change with time, so that there is no observable change in the properties of the system.
 State of Chemical Equilibrium
State of Chemical Equilibrium
- Usually, this state results when the forward reaction proceeds at the same rate as the reverse reaction.
- The reaction rates of the forward and backward reactions are generally not zero, but equal. Thus, there are no net changes in the concentrations of the reactant(s) and product(s). Such a state is known as dynamic equilibrium.
Irreversible Reactions
Those reactions which proceed in forward direction and reaches almost to completion are called Irreversible reactions.
For example:
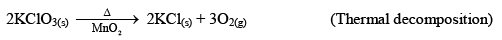
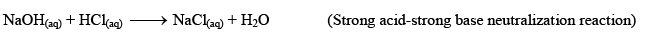
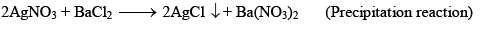
Irreversible Reactions:
- Always goes for completion.
- Reactants are completely consumed in these reactions
- Precipitation reaction, NaCl + AgNO3→AgCl(s) + NaNO3
- If we remove AgCl (which is the product), reaction will move in forward direction.
Reversible Reactions
Those reactions which proceed in both forward and backward directions and never reaches completion are called Reversible reactions.
Examples:
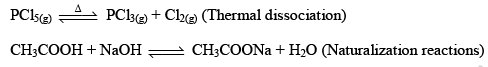

But when Fe(s) is heated and water vapor is passed over it in an open vessel, it is converted to Fe3O4(s) along with the evolution of hydrogen gas.
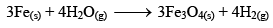
And when Fe3O4 is reduced with hydrogen gas, it gives Fe(s) and H2O
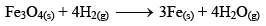
But, if the reaction is carried out in closed vessel, this reaction becomes reversible.
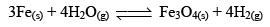
Reversible reactions:
- Never goes for completion
- Irrespective of the fact whether the reaction has started by reactants or products.
 If we remove C (which is product), the reaction will again start and move in the forward direction to attain equilibrium again.
If we remove C (which is product), the reaction will again start and move in the forward direction to attain equilibrium again.
- These reactions can be initiated in any direction.
- Always takes place in a closed vessel.

State of Equilibrium
Equilibrium is a state in which the rate of the forward reaction equals the rate of the backward reaction. Although some chemical reactions reach completion, some other reactions do not completely occur.
Physical Equilibrium (e.g., Vaporization of Water):
- Water evaporates, and vapor concentration increases.
- The rate of evaporation equals the rate of condensation.
- Concentrations of liquid water and vapor remain constant.
- Molecules continue to transition between liquid and vapor phases, but there is no net change in their amounts.
Chemical Equilibrium (e.g., Dissociation of PCl5):
- PCl5 dissociates into PCl3 and Cl2.
- The rates of the forward reaction (PCl5 dissociating) and the reverse reaction (PCl3 and Cl2 recombining) become equal.
- Concentrations of PCl5, PCl3, and Cl2 remain constant.
- Reactions continue in both directions, but the net concentration of each substance does not change.
Key Characteristics of Equilibrium:
- Reactant and product concentrations do not change at equilibrium.
- Molecules continue to react in both directions at the same rate.
- The system can adjust if disturbed, shifting to re-establish equilibrium.
Le Chatelier's Principle:
- If equilibrium is disturbed (by changes in concentration, pressure, or temperature), the system will shift to restore equilibrium.
This can be shown graphically.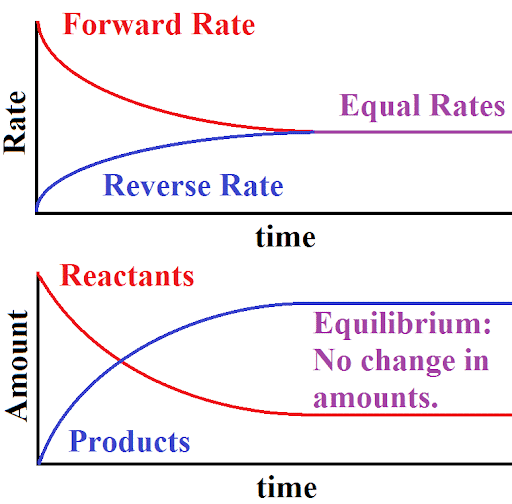
So, “state of chemical equilibrium can be defined as the state when the rate of forward reaction becomes equal to the rate of reverse reaction and the concentration of all the species becomes constant”.
Law of Mass Action
Guldberg and Waage in 1807 gave this law and according to this law, “At constant temperature, the rate at which a substance reacts is directly proportional to its active mass and the rate at which a chemical reaction proceeds is directly proportional to the product of active masses of the reacting species”.
The term active mass of a reacting species is the effective, concentration or its activity (a) which is related to the molar concentration (C) as
a = f C
where f = activity coefficient. F < 1 but f increases with dilution and as V → ∞ i.e. C → 0, f → 1 i.e., a → C Thus at very low concentration the active mass is essentially the same as the molar concentration. It is generally expressed by enclosing the formula of the reacting species in a square bracket.
To illustrate the law of mass action, consider the following general reaction at a constant temperature,
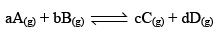
Applying law of mass action,
Rate of forward reaction,
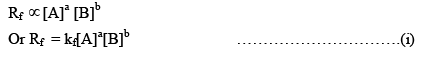
Where kf = rate constant of forward reaction
Similarly,
Rate of reverse reaction

Where kr = rate constant of the reverse reaction.
At equilibrium,
Rate of forward reaction = Rate of reverse reaction
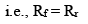
So, from equation (i) and (ii), we get
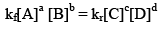
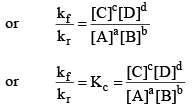
where, Kc is the equilibrium constant in terms of molar concentration.
Illustration: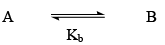 The rate of disappearance of A is given as
The rate of disappearance of A is given as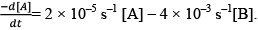 Calculate the value of the equilibrium constant.
Calculate the value of the equilibrium constant.
Solution:
We know, at equilibrium concentration of each species present in the given equilibrium. Become constant.
Equilibrium Constant (Kp) in terms of Partial Pressure:
Consider the same general reaction taking place at a constant temperature,
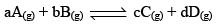
From the law of mass action,

From the ideal gas equation
PV = nRT
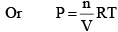
At constant temperature,
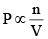
Thus, we can say in a mixture of gases, the Partial pressure of any component (say A)
P ∝[A]
Similarly, P ∝ [B]
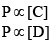
So, equation (1) can be rewritten as

All Equilibrium constants (Keq)-
- Kc
- Kp
- Kx
- Kn
Kx and Kn are not considered equilibrium constants, because these can be varied without change in temperature for gases.
Relationship Between Kp and Kc
From the above, for the same general reaction at constant temperature.

And 
From the ideal gas equation,
PV = nRT
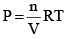
So, PB = [B] RT; PD = [D]RT
Similarly, PA = [A]RT; PC = [C]RT
Substituting the values of PA, PB, PC, and PD in equation (2), we get
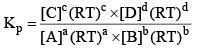
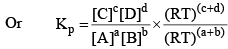

Where, Δn = (c + d) - (a + b)
i.e;, Δn = sum of no. of moles of gaseous products-sum of no. of moles of gaseous reactants.
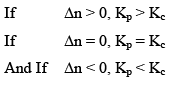
Illustration: The value of Kp for the Reaction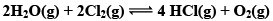 is 0.03 atm at 4270C, when the partial pressure is expressed in atm. What is the value of Kc.
is 0.03 atm at 4270C, when the partial pressure is expressed in atm. What is the value of Kc.
Solution: Firstly, consider species that are present in gaseous phase only. So, we can write Kp.
Homogeneous Reactions:
- All reactants and products are in the same phase (gas, liquid, or solid).
- Example:
Heterogeneous Reactions:
- Reactants and products are in different phases (solid, liquid, or gas).
- Example:
Equilibrium Constant for Homogeneous Reversible Reactions
Products and reactants are in the same phase. Homogeneous gaseous equilibria are best classified into three categories i.e., in which no. of moles of product and reactant varies.
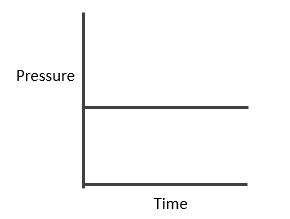
Case I: Homogeneous; Δng = 0
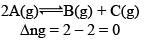
In this reaction, each and every species present are in same phase. That’s why this reaction is under the category of homogeneous equilibria.
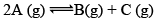
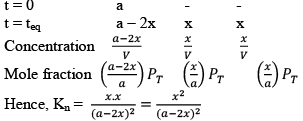
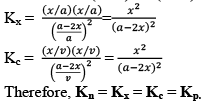
PV = nRT (Ideal gas equation)
Here, V is constant. R is also constant.
P α n
Since no. of moles are constant i.e. Initial = a
Final = a
Hence PT also remains constant and we will get the curve mention below.
Case II: Homogeneous:Δng > 0
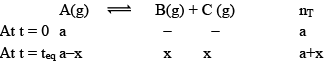
You will easily get these expressions in the same way we did in last.
Here, no. of moles increases at equilibrium i.e. from a to (a+x). Hence PT also increases and becomes constant at equilibrium as shown below.
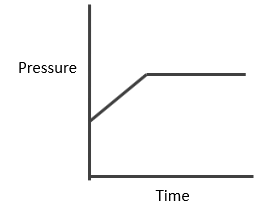
Case III: Homogeneous and Δng < 0
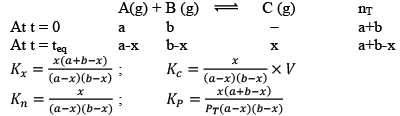
This graph clearly resembles that first pressure decreases and then becomes constant at equilibrium.
Synthesis of Hydrogen Iodide:
Suppose ‘a’ moles of H2 and ‘b’ moles o f I2 are heated at 444°C in a closed container of volume ‘V’ litre and at equilibrium, 2x moles of HI are formed.
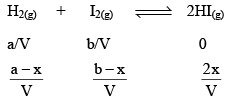
Initial concentration (mol L–1)
Equilibrium concentration (mol L–1)

Substituting the equilibrium concentrations of H2, I2 and HI in equation (i), we get
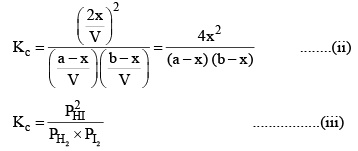
Suppose the total pressure of the equilibrium mixture at 444°C is P, then
PHI = mole fraction of HI × Total pressure
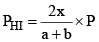
Similarly,
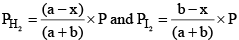
Substituting these values in equation (iii) we get
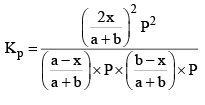
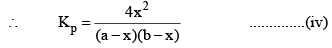
So, one can see from equations (iii) and (iv), that
Kp = Kc
This is so because Δn = 0 for the synthesis of HI from H2 and I2.
Thermal Dissociation of Phosphorus Pentachloride
PCl5(g) dissociates thermally according to the reaction,
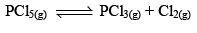
Let us consider that 1 mole of PCl5 has been taken in a container of volume V litre and at equilibrium x moles of PCl5(g) dissociates. Thus
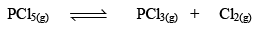
Initial concentration (mo l L–1) 1 0 0 0
Equilibrium concentration (mol L–1) 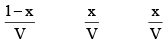
According to law of mass action, at a constant temperature,

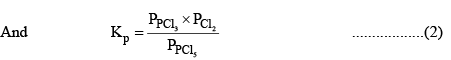
Substituting the values of equilibrium concentration, in equation (1), we have

Now, total number of moles at equilibrium = 1 – x + x + x = 1 + x
Mole fraction of PCl3 = Mole fraction 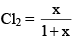
And mole fraction of PCl5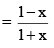
Suppose total pressure at equilibrium is P, then we have from equation (2),
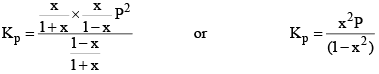
Similarly, we can apply law of mass action on any reaction at equilibrium.
Equilibrium Constant for Heterogeneous Reversible Reactions
The equilibrium which involves reactants and products in different physical states. The law of mass action can also be applied on heterogenous equilibria as it was applied for homogenous equilibria (involving reactants and products in same physical states).
Thermal Dissociation of Solid Ammonium Chloride:
The thermal dissociat ion of NH4Cl(s) takes place in a closed container according to the equation
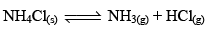
Let us consider 1 mole of NH4Cl(s) is kept in a closed container of volume ‘V’ litre at temperature TK and if x mole of NH4Cl dissociates at equilibrium then

Initial moles 1 0 0
Moles at equilibrium 1- x x x
Applying law of mass action, Kc 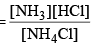
As NH4Cl is a pure solid, so there is no appreciable change in its concentration. Thus,
Kc = [NH3] [HCl]
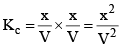
And Kp =PNH3 * PHCl
Thermal Dissociation of Ag2CO3:
Ag2CO3(s) dissociates thermally according to the equation.
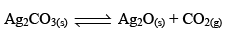
Applying law of mass action, at constant temperature, we get,
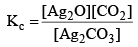
Now, let us consider that 1 mole of Ag2CO3(s) is heated in a closed container of volume V and x mo l of Ag2CO3(s) dissociates at equilibrium, then

Initial moles 1 0 0
Equilibrium moles 1 - x x x
Now, as Ag2CO3 and Ag2O are solids, so their concentration can be assumed to be constants Thus
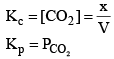
Significance of magnitude of Equilibrium Constant
- A very large value of Kc or Kp signifies that the forward reactions has gone to completion or very nearly so.
- A very small value o f Kc or Kp signifies that the forward reaction has not occur to any significant extent.
- If the numerical value of Kc or Kp is neither very large or very small, a reaction is most likely to reach a state of equillibrium in which both reactants and products are present
Predictions of Direction of the Reaction
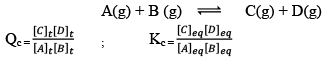
QC is called Reaction Quotient:
QC is the ratio of the concentration of products and reactants each raised to their schoitiometric coefficient as in balanced chemical equation.
Hence, three cases arises:
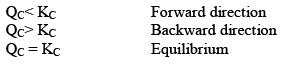
Note: While dealing wit h KP and α, take initial moles of reactant as 1 because ultimately they will be cancelled out.
The Extent of Reaction
Magnitude of equilibrium constant tells us the extent of reaction. It resembles the extent by which the reactant has been reacted or product has been formed at equilibrium.Case I:
If equilibrium constant (say KC) is very-very small.
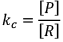
(The concentration of product is very low and the concentration of reactant is very high) It clearly explains that the numerator is very small and denominator is very-very high.
Hence, by this we can infer that reaction has a very low approach in forward direction and reaction has just started.
Case II:
If equilibrium constant (i.e. KC) is very-very high.
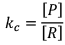
(Concentration of product is very high and concentration of reactant is very low).
Hence, it explains that reaction has almost completed.
Illustration: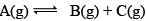 Initial mole of reactant is 1 mole and the volume of the container is 1L. Calculate the moles of B(g) at Equilibrium Kc = 10–50
Initial mole of reactant is 1 mole and the volume of the container is 1L. Calculate the moles of B(g) at Equilibrium Kc = 10–50
Solution: Since the value of KC is very low.
x = 10–25
Illustration: If initially 1 mole of all the species present one taken in 10 L closed vessel, find the equilibrium concentration of each species.
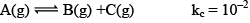
Solution:
At any time concentration
Since QC> KC, so reaction will move in backward direct ion to attain equilibrium.
Equilibrium concentration
Equilibrium concentration of A(g) = 0.16
Equilibrium concentration of B(g) = 0.04
Equilibrium concentration of C(g) = 0.04
Illustration: Calculate KP for the reaction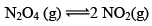 . When NO2 is 30% dissociated and total pressure at equilibrium is 2 bar.
. When NO2 is 30% dissociated and total pressure at equilibrium is 2 bar.
Solution:
Given, α = 0.3
We are dealing with KP and α. Hence initial mole of N2O4 = 1
Partial Pressure
Put α = 0.3
KP = 0.79
Dealing with Degree of Dissociation (α)
In terms of moles
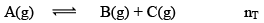
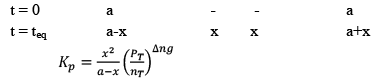
In terms of α
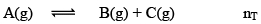
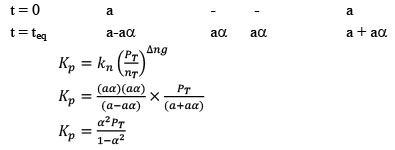
Applications of Chemical Equilibrium
Industrial Chemistry: Chemical equilibrium principles are widely used in industrial processes to optimize reaction yields and product purity. Examples include the Haber-Bosch process for ammonia synthesis and the production of methanol and sulfuric acid.
Environmental Chemistry: Equilibrium concepts play a role in understanding environmental processes, such as the behavior of pollutants in air, water, and soil. Equilibrium calculations help assess factors like pH in natural waters and the equilibria involved in acid rain formation.
Chemical Analysis: Equilibrium-based methods are employed in analytical chemistry for quantitative analysis. Techniques like spectrophotometry and titration rely on equilibria between analytes and reagents to determine concentrations.
Pharmaceuticals: Drug formulations often involve equilibrium-based principles. For example, the solubility of a drug in a particular solvent can be crucial for drug delivery systems.
Biological Systems: Equilibrium concepts are relevant in biological systems, such as the binding of oxygen to hemoglobin in blood. Understanding the equilibrium between reactants and products is essential for comprehending biochemical reactions.
Corrosion Prevention: Equilibrium considerations are important in preventing corrosion. By controlling the conditions in which metals are exposed to moisture and oxygen, it is possible to establish conditions that hinder the corrosion process.
Food Chemistry: Equilibrium reactions are crucial in food chemistry, such as controlling the pH of food products and ensuring the stability of emulsions and suspensions.
Fertilizer Production: In the production of fertilizers, equilibrium principles are applied to optimize the synthesis of nutrients like ammonium nitrate.
|
84 videos|142 docs|67 tests
|
FAQs on Chemical Equilibrium, Law of Mass Action & Applications - Physical Chemistry
| 1. What is chemical equilibrium and how does it differ from irreversible reactions? |  |
| 2. What is the Law of Mass Action and how is it applied in chemical equilibrium? |  |
| 3. How do you calculate the equilibrium constant for homogeneous reversible reactions? |  |
| 4. What is the significance of the magnitude of the equilibrium constant? |  |
| 5. How can the direction of a reaction be predicted using the equilibrium constant? |  |



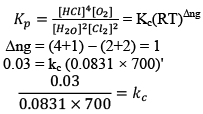
 2HI
2HI