Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Chords & Tangents
Chords & Tangents | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Circles & Chords
What is a chord?
- A chord in a circle is any straight line that joins any two points on the circumference.
- Equal chords are equidistant from the center of the circle. This implies that if each end of a chord is connected to two radii, they will create an isosceles triangle.
- This information is not categorized as a circle theorem, but it is immensely valuable for solving circle theorem problems.
- When tackling circle theorem questions, start by identifying any radii and mark them as equal lines. Then, examine if the radii are connected to any chords.
Circle Theorem: The perpendicular bisector of a chord is a radius
- If a radius or diameter intersects a chord in a circle, it will bisect that chord at a right angle.
- The term "bisect" means to cut something in half.
- This particular circle theorem, although less commonly seen, can be very helpful in determining equal lengths and angles. It is frequently encountered in problems involving congruent triangles.
- To identify this theorem, look for a radius and check if it intersects any chords. Typically, questions related to this theorem involve radii joined to the ends of chords, creating two congruent triangles. This visual representation is easier to comprehend than to recall from a description.
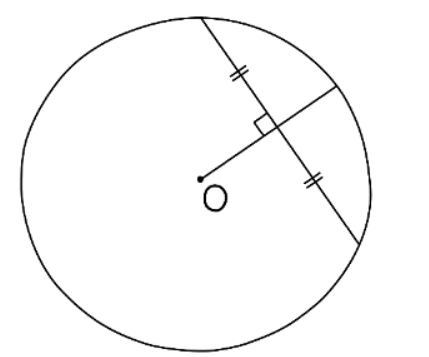
What else should I know about chords?
- Although not categorized as a circle theorem, a significant aspect to note is the formation of an isosceles triangle within a circle.
- Constructing a triangle from the center using a chord and two radii results in an isosceles triangle. This implies that at least two angles will be equal, and there will exist a line of symmetry within the triangle.
- Understanding this property is valuable in proving various circle theorems and can aid in solving geometric puzzles efficiently.
Circles & Tangents
What is a tangent?
- A tangent is a straight line outside a circle that touches the circumference only once.
- Tangents are easy to identify in circle theorem questions as they lie outside the circle distinctly.
Circle Theorem: A radius and a tangent are perpendicular
- In circle theorem questions, a tangent usually intersects a radius where it touches the circle's circumference. It's crucial to confirm the line the tangent intersects is indeed a radius.
- This theorem states that a radius and a tangent meet at a right angle (90 degrees).
- Remember, perpendicular simply means meeting at right angles. When applying this theorem in exams, emphasize the keywords 'A radius and a tangent meet at right angles.'
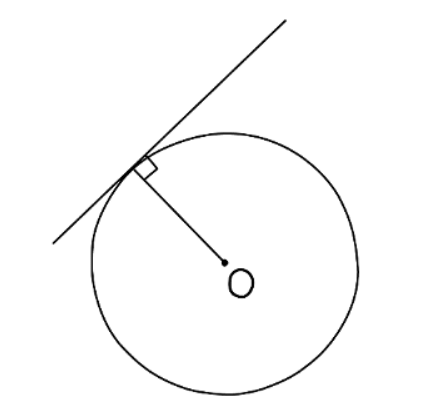
What else should I know about tangents?
- Although not a circle theorem, the following fact is crucial for solving some problems:
- Two tangents drawn from the same external point to a circle are equal in length.
- This forms a kite with the two tangents meeting the circle.
- A kite consists of two congruent triangles along its main diagonal.
- The kite will include two right angles.
- The tangents end at two points: one where they meet outside the circle and the other where each touches the circle.
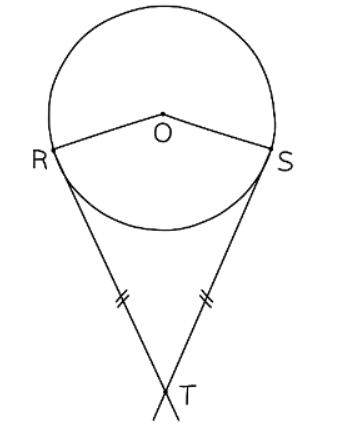
Question for Chords & TangentsTry yourself: What is a chord in a circle?View Solution
The document Chords & Tangents | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
38 videos|413 docs|19 tests
|
FAQs on Chords & Tangents - Mathematics for GCSE/IGCSE - Class 10
| 1. What is the relationship between a chord and a tangent in a circle? |  |
Ans. A chord is a line segment that connects two points on a circle, while a tangent is a line that intersects the circle at only one point. The point of intersection between a tangent and a chord is called the point of tangency.
| 2. How can you determine the length of a chord in a circle? |  |
Ans. The length of a chord in a circle can be determined by using the Pythagorean Theorem or the properties of right triangles formed by the chord and the radius of the circle.
| 3. What is the significance of tangents in relation to circles and chords? |  |
Ans. Tangents are important in circle geometry as they provide a unique point of contact between the circle and a line. They also form right angles with the radius of the circle at the point of tangency.
| 4. How can you find the distance between a chord and a tangent in a circle? |  |
Ans. The distance between a chord and a tangent in a circle can be found by using the formula for the distance between a point and a line. This involves calculating the perpendicular distance from the center of the circle to the line containing the chord.
| 5. What are some real-world applications of circles, chords, and tangents? |  |
Ans. Circles, chords, and tangents have various applications in fields such as architecture, engineering, and physics. For example, circles are used to design roundabouts, while tangents are utilized in the construction of bridges to ensure smooth curves and angles.
Related Searches















