Circle Theorems | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Introduction |

|
| Angle Subtended by a Chord at a Point |

|
| Perpendicular from the Centre to a Chord |

|
| Equal Chords and Distance from the Centre |

|
| Cyclic Quadrilaterals |

|
Introduction
Circle is a collection of points that are at a fixed distance from a particular point. The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle.
 Circle
Circle
We come across many objects in real life which are round in shape. For example, wheels of vehicles, bangles, dials of telephone, etc. In the clock also, its hands move in a round fashion repeatedly. The path traced by the tip of the hands of the clock is called a circle.
Let’s look at some terminology related to a circle in brief:
- Arc: A piece of a circle between two points is called an arc.
- Chord: If you take two points I and J on a circle, then the line segment IJ is called a chord of the circle.
- Circumference: The length of the complete circle is called its circumference.
- Segment: The region between a chord and either of its arcs is called a segment of the circular region or simply a segment of the circle.

Angle Subtended by a Chord at a Point
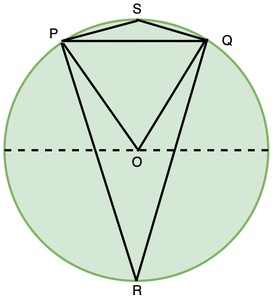 Take a chord in the figure above PQ. R and S are two points on the circle. ∠PRQ is called angle subtended by chord PQ on point R. Similarly chord subtends angles on S and also on the centre of the circle O. Let’s study the relationships between angles subtended by chord PQ on these points.
Take a chord in the figure above PQ. R and S are two points on the circle. ∠PRQ is called angle subtended by chord PQ on point R. Similarly chord subtends angles on S and also on the centre of the circle O. Let’s study the relationships between angles subtended by chord PQ on these points.
Theorem 1: Equal chords of circle subtend equal angles at the centre.
Given:
A circle with centre H.
Two chords KL and JI are equal
To Prove: ∠KHL = ∠JHI
Proof:
We are given two chords KL and JI. We need to prove that ∠KHL = ∠JHI.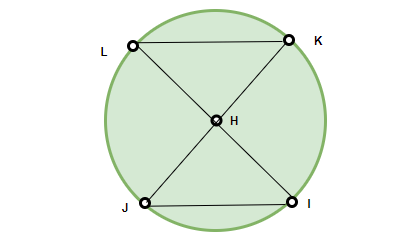 In triangles KHL and JHI,
In triangles KHL and JHI,
HL = HJ
HI = HK
and we are given that KL = JI.
So, both the triangles are congruent. Thus, both of these angles are equal. Hence, proved.
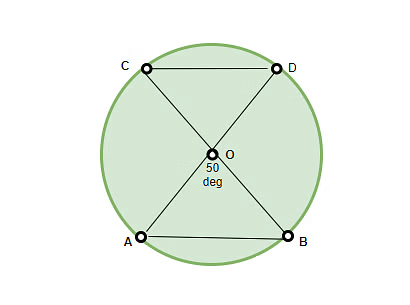
Example 1: If ∠AOB = 50° in the figure given below, what will be the angle subtended by ∠COD, provided that the chords AB and CD are equal.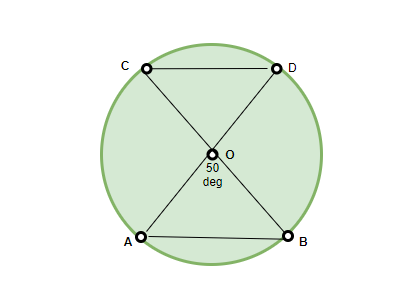 Solution: According to the theorem mentioned above, the angles ∠AOB and ∠COD are equal, since they are equal chords subtending equal angles at the centre. Therefore, ∠COD = 50°.
Solution: According to the theorem mentioned above, the angles ∠AOB and ∠COD are equal, since they are equal chords subtending equal angles at the centre. Therefore, ∠COD = 50°.
Theorem 2: If the angles subtended by two chords at the centre are equal, then the two chords are equal
Given:
A circle with centre O.
∠COD= ∠AOB are equal
To Prove: AB=CD
Proof:
We are given two chords AB and CD. We need to prove that two chords AB and CD are equal
∠AOB = ∠COD (Equal angle subtended at centre O) ……………(1)
OA = OB = OP = OQ (Radii of the same circle) ……………(2)
From eq. 1 and 2, we get;
∆AOB ≅ ∆POQ (SAS Axiom of congruency)
Hence,
AB = PQ (By CPCT)
Perpendicular from the Centre to a Chord
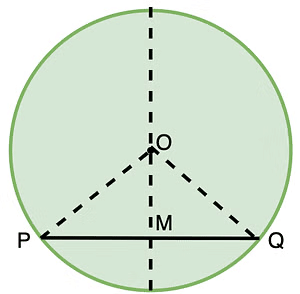
Theorem 3: The perpendicular from the centre of a circle to a chord bisects the chord
 Given:
Given:
A circle with centre O.
PQ is a chord such that OM is perpendicular to PQ
To Prove: OM bisects chord PQ i.e. PM=MQ
Proof: Given, in ∆AOD and ∆BOD,
∠ADO = ∠BDO = 90° (OD ⊥ AB) ………(1)
OA = OB (Radii of the circle) ……….(2)
OD = OD (Common side) ………….(3)
From eq. (1), (2) and (3), we get;
∆AOB ≅ ∆POQ (R.H.S Axiom of congruency)
Hence, AD = DB (By CPCT)
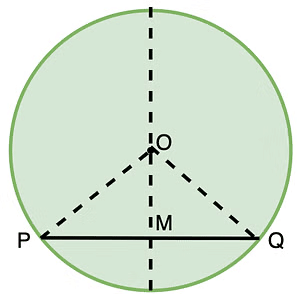
Theorem 4: The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord
Given:
A circle with centre O.
OM bisects chord PQ i.e. PM=MQ
To Prove: PQ is a chord such that OM is perpendicular to PQ
Proof:
Let PQ be the chord of a circle and OM be the line from the centre that bisects the chord. Here, M is the mid point of the chord, and we have to prove that ∠OMQ = 90°.
In triangles ΔOPM and ΔOQM.
PM = MQ (perpendicular bisects the chord)
OP = OQ (radius of the circle)
OM = OM (common side of both the triangles)
So, both these triangles are congruent. This gives, angles ∠OMQ and ∠OMP as 90°
Equal Chords and Distance from the Centre
If two chords of a circle are equal, then their corresponding arcs are congruent and conversely, if two arcs are congruent, then their corresponding chords are equal. Similar to the case of chords, equal arcs also subtend equal angles at the centre.
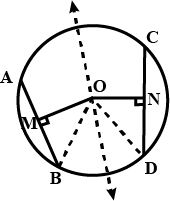
Theorem 5: Equal chords of a circle are equidistant (equal distance) from the centre of the circle.
Given:
A circle with centre O.
AB and CD are two equal chords of a circle i.e. AB=CD and OM and ON are perpendiculars to AB and CD respectively.
To Prove: OM=ON
Proof:
Given, In ∆OMB and ∆OND
BM = 1/2 AB (Perpendicular to a chord bisects it) ……..(1)
DN = 1/2 CD (Perpendicular to a chord bisects it) ……..(2)
AB = CD (Given)
BM = DN (from eq 1 and 2)
OB = OD (Radii of the same circle)
∠OMB = ∠OND = 90° (OM ⊥ AB and ON ⊥ CD)
∆OMB ≅ ∆OND ( By R.H.S Axiom of Congruency)
Hence, OM = ON ( By CPCT)
Theorem 6: Chords of a circle, which are at equal distances from the centre are equal in length
 Given:
Given:
A circle with centre O.
AB and CD are two equal chords of a circle i.e. AB=CD and OM and ON are perpendiculars to AB and CD respectively.
OM=ON
To Prove: AB=CD
Proof: Given, in ∆OMB and ∆OND, OM = ON ………….(1)
∠OMB = ∠OND = 90° ………..(2)
OB = OD (Radii of the same circle) ………..(3)
Therefore, from eq. 1, 2 and 3, we get;
∆OMB ≅ ∆OND (By R.H.S Axiom of Congruency)
BM = DN ( By CPCT)
1/2 AB = 1/2 CD (Perpendicular from center bisects the chord)
Hence, AB = CD
Theorem 7: The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Given: An arc PQ of a circle subtending angles POQ at the centre O and PAQ at a point A on the remaining part of the circle.
To Prove :∠POQ = 2∠PAQ.
Proof:
Let’s consider three cases,
- Arc PQ is major arc.
- Arc PQ is minor arc.
- Arc PQ is semi-circle.
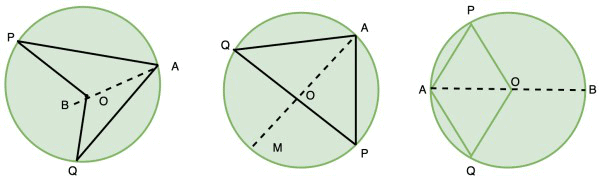
Let’s join AO and extend it to B.
In all three cases, ∠BOQ = ∠OAQ + ∠OQA. (Exterior angle of a triangle is equal to the sum of the two interior opposite angles).
Also in triangle ΔOAQ,
OA = OQ (Radii of Circle)
Therefore, ∠ OAQ = ∠ OQA
this gives, ∠ BOQ = 2∠OAQ
∠ BOP = 2∠OAP
from (1) and (2), ∠ BOP + ∠ BOQ = 2(∠ OAP + ∠ OAQ)
∠POQ = 2 ∠PAQ
For the case (iii), where PQ is the major arc, (3) is replaced by
Reflex angle POQ = 2∠PAQ
Example 2: What is the value of ∠ABC?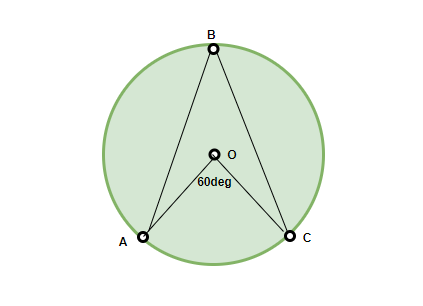 Solution: According to the theorem, ∠AOC = 2 ∠ABC
Solution: According to the theorem, ∠AOC = 2 ∠ABC
Therefore, ∠ABC = 60°/2 = 30°
Some other properties
- Angles in the same segment of a circle are equal.
- If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e. they are concyclic).
Cyclic Quadrilaterals
A quadrilateral is called cyclic if all the four vertices of it lie on a circle. They are also called inscribed quadrilaterals.
They are also called inscribed quadrilaterals.
Theorem 8: Angles in the same segment of a circle are equal.
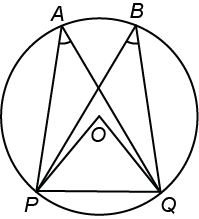
Given:
A circle with centre O
Points P and Q on this circle subtends ∠PAQ = ∠PBQ at points A and B respectively.
To Prove : ∠PAQ = ∠PBQ
Proof: Let P and Q be any two points on a circle to form a chord PQ, A and C any other points on the remaining part of the circle and O be the centre of the circle. Then,
∠POQ = 2∠PAQ ...... (i)
And ∠POQ = 2∠PCQ ....... (ii)
From above equations, we get
2∠PAQ = 2∠PCQ
Hence ∠PAQ = ∠PCQ
Theorem 9: If a line segment joining two points subtend equal angles at two other points lying on the same side of the lien containing the line segment the four points lie on a circle.
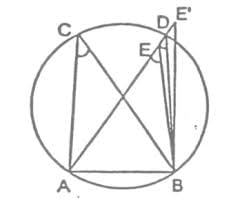 Given:
Given:
AB is a line segment, which subtends equal angles at two points C and D. i.e., ∠ACB = ∠ADB.
To Prove:
The points A, B, C and D lie on a circle.
Proof:
Let us draw a circle through the points A, C and B.
Suppose it does not pass through the point D.
Then it will intersect AD (or extended AD) at a point, say E (or E’).
If points A,C,E and B lie on a circle,
∠ACD = ∠AEB [∴ Angles in the same segment of circle are equal]
But it is given that ∠ACB = ∠ADB
Therefore, ∠AEB = ∠ADB
This is possible only when E coincides with D. [As otherwise ∠AEB >∠ADB]
Similarly, E’ should also coincide with D. So A, B, C and D are concyclic.
Hence Proved.
Theorem 10: The sum of either pair of opposite angles of a cyclic quadrilateral is 180º.
Given: PQRS is a cyclic quadrilateral with centre O.
To Prove:
∠PSR + ∠PQR = 360°
∠SPQ + ∠QRS = 360°
Proof: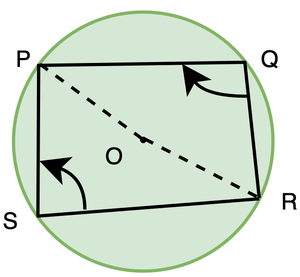 Considering arc PQR, ∠POR = 2 ∠PSR,
Considering arc PQR, ∠POR = 2 ∠PSR,
Similarly, considering PSR, reflex ∠POR = 2∠PQR
We know, ∠POR + relfex ∠POR = 360°.
⇒ 2 ∠PSR + 2∠PQR = 360°
⇒ 2(∠PSR + ∠PQR) = 360°
⇒ ∠PSR + ∠PQR = 180°
Thus, sum of opposite angles of cyclic quadrilateral is 180°.
Example 3: In the figure below, BC is the diameter of the circle, ED is a chord equal to the radius of the circle. BE and CD when extended intersect at a point F. Prove that ∠BFC = 60°.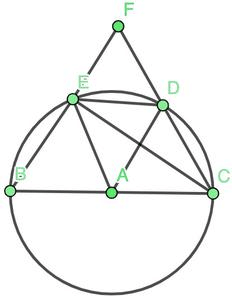 Solution: In the figure, join AE, AD and EC. Triangle AED is an equilateral triangle.
Solution: In the figure, join AE, AD and EC. Triangle AED is an equilateral triangle.
Therefore, ∠EAD = 60°. Now, ∠ECD becomes 30°.
We know that ∠BEC = 90°.
So, by the property of exterior angles of triangle,
∠BEC = ∠ECD + ∠BFC,
90° = 30° + ∠BFC
⇒ 60° = ∠BFC
Hence, Proved.
Theorem 11: If the sum of a pair of opposite angles of a quadrilateral is 180º, the quadrilateral is cyclic.
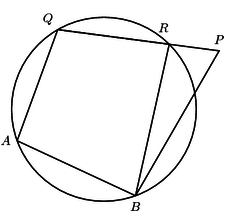
Given: ABPQ is a quadrilateral, such that ∠ ABP + ∠ AQP =180 ∘ and ∠ QAB + ∠ QPB = 180 ∘
To prove: The points A, B, P and Q lie on the circumference of a circle.
Proof: Assume that point P does not lie on a circle drawn through points A, B and Q.
Let the circle cut QP at point R. Join BR. ∠ QAB + ∠ QRB = 180 ∘ [opposite angles of cyclic quadrilateral.]
∠ QAB + ∠ QPB = 180 ∘ [given]
∴ ∠ QRB = ∠ QPB
But this cannot be true since ∠ QRB = ∠ QPB + ∠ RBP (exterior angle of the triangle)
∴ Our assumption that the circle does not pass through P is incorrect and A, B, P and Q lie on the circumference of a circle.
∴ ABPQ is a cyclic quadrilateral.
Example 4 :In the figure, PQRS is a cyclic quadrilateral where PR and QS are its diagonals. If ∠ QPR = 60° and ∠ PSR = 50°, find ∠ QRS.
Solution:
- PQRS is a cyclic quadrilateral.
- PR and QS are diagonals.
- ∠ QPR = 60°.
- ∠ PSR = 50°.
We need to find ∠ QRS.
Step-by-Step Solution:
In a cyclic quadrilateral, opposite angles add up to 180° because of the property of cyclic quadrilaterals (sum of opposite angles is supplementary).
In triangle PQR, by using the property of cyclic quadrilaterals, we can write:
∠ QPR + ∠ QRS = 180° (since diagonally opposite angles in a cyclic quadrilateral are supplementary).
Substituting the given values:
60° + ∠ QRS = 180°
Solving for ∠ QRS:
∠ QRS = 180° - 60° = 120°
Thus, the measure of ∠ QRS is 120°.
Example 5: Prove that the quadrilateral formed by the internal angle bisectors of any quadrilateral is cyclic.
Solution:
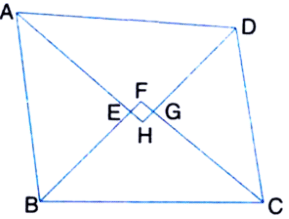
ABCD is a quadrilateral in which the angle bisectors AH, BF, CF and DH of internal angles A, B, C and D respectively form a quadrilateral EFGH.
Now, ∠ FEH = ∠ AEB = 180° – ∠ EAB – ∠ EBA (Why ?)
= 180° – 1/ 2 (∠ A + ∠ B)
and ∠ FGH = ∠ CGD = 180° – ∠ GCD – ∠ GDC (Why ?)
= 180° – 1 /2 (∠ C + ∠ D)
∠ FEH + ∠ FGH = 180° – 1 /2 (∠ A + ∠ B) + 180° – 1/ 2 (∠ C + ∠ D)
= 360° – 1/ 2 (∠ A+ ∠ B +∠ C +∠ D) = 360° – 1 /2 × 360°
= 360° – 180° = 180°
Therefore, by Theorem 11, the quadrilateral EFGH is cyclic.
Example 6: Two circles intersect at two points B and C. Line segments ABD and PBQ are drawn through B, intersecting the circles at points A, D, and P, Q, respectively. Prove that ∠ACP = ∠QCD.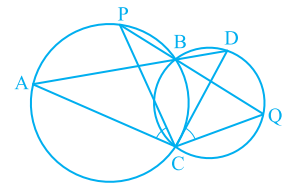
Solution:
Given:
- Two intersecting circles at points B and C.
- Line segments ABD and PBQ intersect the circles at points A, D and P, Q respectively.
To Prove:
∠ACP = ∠QCDWe will use the properties of cyclic quadrilaterals and the intersecting chords theorem to prove this.
Step 1: Recognizing the Cyclic Quadrilaterals
- Since A, B, C, D lie on one circle, quadrilateral ABCD is a cyclic quadrilateral.
- Similarly, P, B, C, Q lie on another circle, so quadrilateral PBCQ is also cyclic.
Step 2: Properties of Cyclic Quadrilaterals
In any cyclic quadrilateral, the opposite angles are supplementary (i.e., their sum is 180°).
In ABCD, we have:
∠ABC+∠ADC=180°In PBCQ, we have:
∠PBC+∠PQC=180°
Step 3: Using the Common Angle ∠ABC = ∠PBC
Since B is a common point on both quadrilaterals, ∠ABC = ∠PBC.
Step 4: Angle Chasing
In cyclic quadrilateral ABCD:
- ∠ACP and ∠ADC subtend the same arc AC in the circle, so they are equal.
Therefore, ∠ACP = ∠ADC.
In cyclic quadrilateral PBCQ:
- ∠QCD and ∠PQC subtend the same arc QC, so they are equal.
Therefore, ∠QCD = ∠PQC.
Step 5: Conclusion
Since ∠ACP = ∠ADC and ∠QCD = ∠PQC, and both angles subtend the same arcs in their respective circles, we conclude that:
|
40 videos|471 docs|57 tests
|
FAQs on Circle Theorems - Mathematics (Maths) Class 9
| 1. What is the angle subtended by a chord at a point outside the circle? |  |
| 2. How can we find the perpendicular distance from the center of a circle to a chord? |  |
| 3. What is the relationship between equal chords and their distance from the center of the circle? |  |
| 4. What is a cyclic quadrilateral and how is it related to circle theorems? |  |
| 5. Can you explain the significance of circle theorems in geometry? |  |





















