Circles: Introduction and Solved Examples | Quantitative Reasoning for GRE PDF Download
Circle
A circle is a simple closed figure in which all the points that lie on it are equidistant from a point called center.
 A Circle
A Circle
A point on the edge is “on the circle”, but a point in the middle part is “in the circle” or “inside the circle.” In the diagram below,
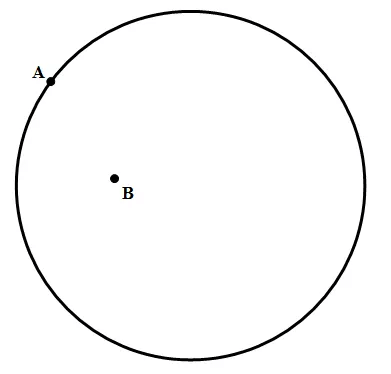 Point A is on the circle, but point B is in the circle.By far, the most important point in the circle is the center of the circle, the point equidistance from all points on the circle.
Point A is on the circle, but point B is in the circle.By far, the most important point in the circle is the center of the circle, the point equidistance from all points on the circle.
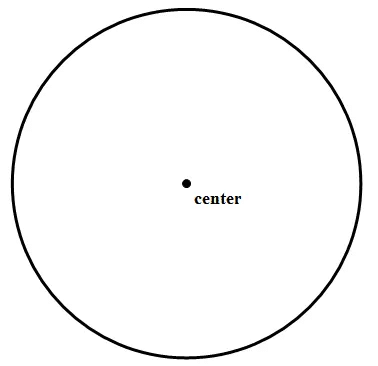 Center of a Circle
Center of a Circle
Here are some basics regarding the circle and its properties:
Basic Terminology
Radius:
The line segment that connects the center of the circle to any point on the circle is called radius. An infinite number of radii can be drawn for any circle.
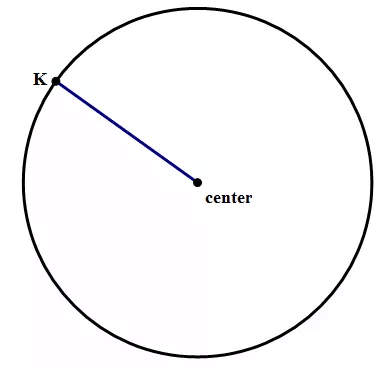 Radius of a Circle
Radius of a Circle
- As is probably clear visually, the radius is exactly half the diameter, because a diameter can be divided into two radii.
- The radius is crucially important because if you know the radius, it’s easy to calculate not only the diameter but also the other two important quantities associated with a circle: the circumference and the diameter.
Diameter:
The line segment that passes through the center and connects two points on the circle is called the diameter.
- AB is the diameter of the circle. Like radius, infinite number of diameters can be drawn in a circle.
- Diameter = 2 * radius
- Radius = Diameter / 2
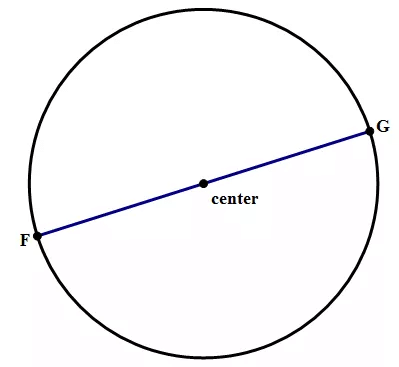 Diameter of a Circle
Diameter of a Circle
Chord:
The line segment that connects any two points on a circle is a chord. Infinite number of chords can be drawn in a circle. XY is a chord of the circle.
Apparently, the diameter is the longest chord of a circle.
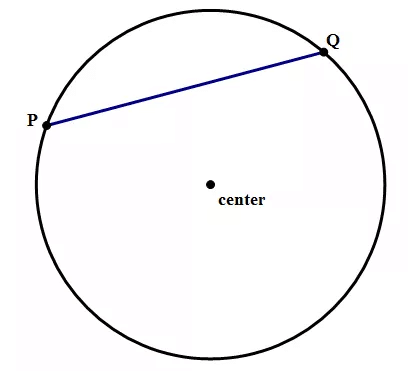 Chord
Chord
- By the way, the word “chord” in this geometric sense is actually related to “chord” in the musical sense: the link goes back to Mr. Pythagoras (c. 570 – c. 495 BCE), who was fascinated with the mathematics of musical harmony.
- If the chord passes through the center, this chord is called a diameter. The diameter is a chord. Diameter is the longest possible chord. Diameter is the only chord that includes the center of the circle.
Circumference:
The measure of the distance around the edge of a circle is the circumference of the circle.
- The circumference of a circle is given by the formula,
C = 2πr - Where C is the circumference and r is the radius.
- Since 2*radius = diameter, Circumference is also given by
C = πd - The value of p is approximately 22/7 or 3.14159.
Area:
The area of a circle is given by the formula,
A = πr2
- Where r is the radius of the circle.
Since r=d/2, - Area is also given by
A = πd2/4
Arcs and Sectors:
Arc: An arc is a part of the circumference of the circle. XY is an arc in the figure below.
Sector: A sector is an area covered by two radii and the arc connecting them. XLY and XOY are two of the sectors in the figure below.
 A sector is an area covered by two radii and the arc connecting them. XLY and XOY are two of the sectors in the figure above.
A sector is an area covered by two radii and the arc connecting them. XLY and XOY are two of the sectors in the figure above.- Length of an arc is given by the formula, (x/360) * 2πr
- Area of a sector is given by the formula, (x/360) * πr2
Where x is the angle subtended by the arc and r is the radius.
Angles:
Central Angle: The angle whose one vertex lies on the center of the circle is a central angle. ∠XOY is a central angle in the figure above.
Inscribed angle: The angle whose one vertex lies on one part of the circle and the other two endpoints lie on another place on the circle, is called an inscribed angle. ∠XLY, ∠OXY, ∠OYX are some of the inscribed angles in the figure above.
Inscribed angles subtended by the same arc are equal.
A central angle is twice the corresponding inscribed angle.
In the figure above,
∠XOY = 2 ∠XLY
Tangent:
A tangent of a circle is a line that just touches the circle at one point without intersecting it. MN is the tangent in the figure above.
Circumscribed Circle
If a polygon is present inside a circle in such a way that all its vertices lie on the circle, or just touch the circle, then the circle is called a circumscribed circle.
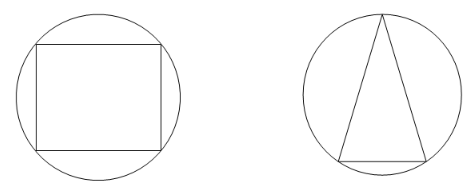
Note: When a triangle is inscribed inside a circle and if one of the sides of the triangle is diameter of the circle, then the diameter acts as hypotenuse and the triangle is right. This is called the Thales’ theorem.
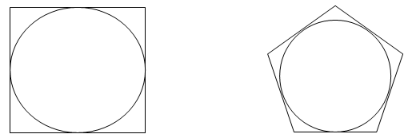
Inscribed Circle
If a circle is present inside a polygon in such a way that the sides of the polygon are just touching the circumference of the circle then the circle is called an inscribed circle.
Semicircle
A semi-circle is half the circle.
Area of a semicircle = πr2 / 2
Circumference of a semicircle = Half the perimeter of a circle + length of the diameter
→ (2πr/2) + 2r
→ πr+2r
→ r(2+π)
Solved Examples Involving Circles
Problem 1: The area of the circle above is 81p. ∠DAB = 55°. Find the central angle subtended by arc DB and the area and circumference of the sector DOB. 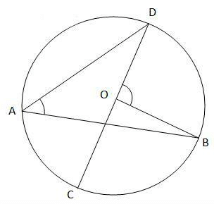
Solution:
Area of the circle = πr2 = 81p
→ r2 = 81 and r = 9.
∠DAB is the inscribed angle subtended by the arc DB. Inscribed angle is half the central angle.
∠DAB = 55° → ∠DOB = 110°.
Area of the sector DOB = (110/360)*81p = 24.75 p
Circumference of the sector is the length of the two radii + length of the arc DB
Length of the arc DB = (110/360)*2*p*9 = 5.5 p
Circumference of the sector DOB = 9 + 9 + 5.5p = 18 + 5.5p
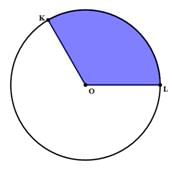
In the shaded region above, ∠KOL = 120°, and the area of the entire circle is A= 144 π. The perimeter of the shaded region is
Problem 2: If QS is the diameter and QR = 6 and radius = 5, find the area of the shaded region.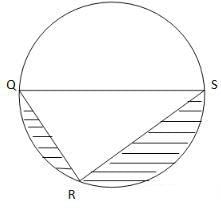
Solution:
Area of the shaded region = Area of the circle – (Area of the triangle QRS + Area of the semicircle)
Area of the circle = 25p
Area of the semicircle = 12.5p
Finding the area of the triangle:
According to Thales’ theorem, if the diameter is the side of a triangle, then it becomes the hypotenuse and the triangle is right.
Therefore, ∠QRS = 90°.
Radius = 5 → Diameter, QS = 10
QR = 6 (given)
According to Pythagoras theorem, QS2 = QR2 + RS2
100 = 36 + RS2 → RS = 8. We can also see that this triplet is a multiple of the famous Pythagorean triplet 3, 4, 5.
Area of a triangle = base * height / 2 = 48 / 2 = 24
Area of the shaded region = 25p – (24 + 12.5p) = (12.5p – 24) sq. units.
What is the radius of the circle?
Statement 1: A=B=5
Statement 2: The circle passes through the origin.
Problem 3: Given that a “12-inch pizza” means circular pizza with a diameter of 12 inches, changing from an 8-inch pizza to a 12-inch pizza gives you approximately what percent increase in the total amount of pizza?
a) 33
b) 50
c) 67
d) 80
e) 125
Answer: E
Solution: The 8-inch pizza has a radius of r = 4, so the area is 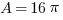 . That area is how much pizza you get. The 12-inch pizza has a radius of r = 6 and an area of
. That area is how much pizza you get. The 12-inch pizza has a radius of r = 6 and an area of 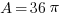 . When you change from 16 to 36, what is the percentage change? Well, that’s more than double, so it must be a percent greater than 100%. The only answer choice greater than 100% is answer E.
. When you change from 16 to 36, what is the percentage change? Well, that’s more than double, so it must be a percent greater than 100%. The only answer choice greater than 100% is answer E.
Problem 4: Data Sufficiency Question
Calculate the area of a circle.
1. The radius of the circle is 4.
2. The circumference of the circle is 24.
Possible Answers:
a) Both statements taken together are sufficient to answer the question, but neither statement alone is sufficient
b) Statement 2 alone is sufficient, but statement 1 alone is not sufficient to answer the question
c) Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question
d) Statements 1 and 2 together are not sufficient, and additional data is needed to answer the question
e) Each statement alone is sufficient
Answer: E
Solution:
The area of a circle can be calculated using the equation: A=r2π
and the circumference calculated using: C=2rπ
The radius is the only information required for calculating the area of a circle and that can be obtained from the circumference, therefore, either statement is sufficient.
Problem 5: Data Sufficiency Question
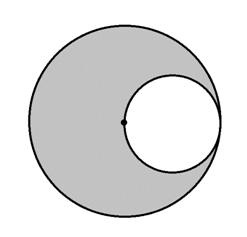
What is the area of the gray region in the above figure?
Statement 1: The diameter of the larger circle is one mile.
Statement 2: The radius of the smaller circle is 1,320 feet.
Possible Answers:
a) BOTH statements TOGETHER are insufficient to answer the question.
b) BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
c) Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
d) Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
e) EITHER statement ALONE is sufficient to answer the question.
Answer: EITHER statement ALONE is sufficient to answer the question.
Explanation: The radius of the larger circle is equal to the diameter of the smaller, and, subsequently, twice the radius of the smaller. If one radius is known, then the other can be calculated, and the areas of the two circles can be as well; the difference between their areas is the area of the gray region. Statement 1 tells us the diameter of the large circle, from which its radius can be determined by dividing by 2; Statement 2 tells us the radius of the smaller circle. From either, the radius of the other circle can be calculated.
|
93 videos|77 docs|104 tests
|
FAQs on Circles: Introduction and Solved Examples - Quantitative Reasoning for GRE
| 1. What is the definition of a circle? |  |
| 2. How do you find the circumference of a circle? |  |
| 3. What is the difference between a radius and a diameter of a circle? |  |
| 4. How is the area of a circle calculated? |  |
| 5. Can the radius of a circle be negative? |  |

|
Explore Courses for GRE exam
|

|
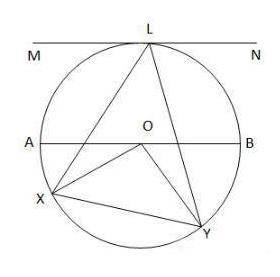 A sector is an area covered by two radii and the arc connecting them. XLY and XOY are two of the sectors in the figure above.
A sector is an area covered by two radii and the arc connecting them. XLY and XOY are two of the sectors in the figure above.
















