Class 8 Maths - Factorisation CBSE Worksheets Solutions
Multiple Choice Questions
Q1:The radius of a circle is 7ab – 7bc – 14a cm, then circumference of the circle is (Given π = 22/7)
(a) 22(ab -bc-2a)
(b) 44(ab -bc-2a)
(c) (ab -bc-2a)
(d) None of these
Ans: (b)
Q2: Factorised form of x2 − (p − 5) x − 5p is
(a) (x-5)(x-p)
(b) (x+5)(x+p)
(c) (x-p)(x+5)
(d) (x+p)(x-5)
Ans: (a)
Q3: Factorised form of r2 – 10 r + 21 is
(a) (r - 7) (r - 3)
(b) (r -7) (r +3)
(c) (r +1) (r - 4)
(d) (r -1) (r - 4)
Ans: (a)
Q4: The expression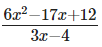 is
is
(a) (2x+3)
(b) (3x+2)
(c) (2x -3)
(d) (3x-2)
Ans: (c)
True and False
Q1: x2 + 4x + 3 is factorized as (x+1) (x+3)
Ans: True
Q2: x2 + (a + b) x + ab = (a + b) (x + ab)
Ans: False
Q3: h is a factor of 2π (h + r).
Ans: False
Q4: Factors of (96 − 4 x − x2) is (x+12)(8-x)
Ans: True
Q5: Common factor of 17 abc, 34 ab2, 51a2b is 17ab
Ans: True
Fill in the Blanks
Q1: −x + x3 is factorised as ______
Ans: x(x-1)(x+1)
Q2: 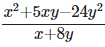 __________
__________
Ans: (x- 3y)
Q3: Factorised form of (x-10)(x+7) + 16 is _______
Ans: (x-9)(x+6)
Q4: Factorised form of 23xy – 46x + 54y – 108 is _____
Ans: (23x + 54) (y – 2)
Q5: Factorized form of a12 x4 − a4 x12 is ____________
Ans: a4x4(a4 + x4)(a2+x2) (a+x) (a−x)
Answer the following Questions
Q1: Find the common factors of the following terms.
(a) 25x2y, 30xy2
(b) 63m3n, 54mn4
Ans:
(a) 25x2y, 30xy2
25x2y = 5 × 5 × x × x × y
30xy2 = 2 × 3 × 5 × x × y × y
Common factors are 5× x × y = 5 xy
(b) 63m3n, 54mn4
63m3n = 3 × 3 × 7 × m × m × m × n
54mn4 = 2 × 3 × 3 × 3 × m × n × n × n × n
Common factors are 3 × 3 × m × n = 9mn
Q2: Factorise the following expressions.
(a) 54m3n + 81m4n2
(b) 15x2y3z + 25x3y2z + 35x2y2z2
Ans:
(a) 54m3n + 81m4n2
= 2 × 3 × 3 × 3 × m × m × m × n + 3 × 3 × 3 × 3 × m × m × m × m × n × n
= 3 × 3 × 3 × m × m × m × n × (2 + 3 mn)
= 27m3n (2 + 3mn)
(b) 15x2y3z + 25 x3y2z + 35x2y2z2 = 5x2y2z ( 3y + 5x + 7)
Q3: Factorise the following polynomials.
(a) 6p(p – 3) + 1 (p – 3)
(b) 14(3y – 5z)3 + 7(3y – 5z)2
Ans:
(a) 6p(p – 3) + 1 (p – 3) = (p – 3) (6p + 1)
(b) 14(3y – 5z)3 + 7(3y – 5z)2
= 7(3y – 5z)2 [2(3y – 5z) +1]
= 7(3y – 5z)2 (6y – 10z + 1)
Q4: Factorise the following:
(a) p2q – pr2 – pq + r2
(b) x2 + yz + xy + xz
Ans:
(a) p2q – pr2 – pq + r2
= (p2q – pq) + (-pr2 + r2)
= pq(p – 1) – r2(p – 1)
= (p – 1) (pq – r2)
(b) x2 + yz + xy + xz
= x2 + xy +xz + yz
= x(x + y) + z(x + y)
= (x + y) (x + z)
Q5: Factorise the following polynomials.
(a) xy(z2 + 1) + z(x2 + y2)
(b) 2axy2 + 10x + 3ay2 + 15
Ans:
(a) xy(z2 + 1) + z(x2 + y2)
= xyz2 + xy + 2x2 + zy2
= (xyz2 + zx2) + (xy + zy2)
= zx(yz + x) + y(x + yz)
= zx(x + yz) + y(x + yz)
= (x + yz) (zx + y)
(b) 2axy2 + 10x + 3ay2 + 15
= (2axy2 + 3ay2) + (10x + 15)
= ay2(2x + 3) +5(2x + 3)
= (2x + 3) (ay2 + 5)
Q6: Factorise the following expressions.
(а) x2 + 4x + 8y + 4xy + 4y2
(b) 4p2 + 2q2 + p2q2 + 8
Ans:
(a) x2 + 4x + 8y + 4xy + 4y2
= (x2 + 4xy + 4y2) + (4x + 8y)
= (x + 2y)2 + 4(x + 2y)
= (x + 2y)(x + 2y + 4)
(b) 4p2 + 2q2 + p2q2 + 8
= (4p2 + 8) + (p2q2 + 2q2)
= 4(p2 + 2) + q2(p2 + 2)
= (p2 + 2)(4 + q2)
Q7: Factorise:
(a) a2 + 14a + 48
(b) m2 – 10m – 56
Ans:
(a) a2 + 14a + 48
= a2 + 6a + 8a + 48
[6 + 8 = 14 ; 6 × 8 = 48]
= a(a + 6) + 8(a + 6)
= (a + 6) (a + 8)
(b) m2 – 10m – 56
= m2 – 14m + 4m – 56
[14 – 4 = 10; 4 × 4 = 56]
= m(m – 14) + 6(m – 14)
= (m – 14) (m + 6)
Q8: Factorise:
(a) x4 – (x – y)4
(b) 4x2 + 9 – 12x – a2 – b2 + 2ab
Ans:
(a) x4 – (x – y)4
= (x2)2 – [(x – y)2]2
= [x2 – (x – y)2] [x2 + (x – y)2]
= [x + (x – y] [x – (x – y)] [x2 + x2 – 2xy + y2]
= (x + x – y) (x – x + y)[2x2 – 2xy + y2]
= (2x – y) y(2x2 – 2xy + y2)
= y(2x – y) (2x2 – 2xy + y2)
(b) 4x2 + 9 – 12x – a2 – b2 + 2ab
= (4x2 – 12x + 9) – (a2 + b2 – 2ab)
= (2x – 3)2 – (a – b)2
= [(2x – 3) + (a – b)] [(2x – 3) – (a – b)]
= (2x – 3 + a – b)(2x – 3 – a + b)
Q9: Factorise the following polynomials.
(a) 16x4 – 81
(b) (a – b)2 + 4ab
Ans: (a) 16x4 – 81
= (4x2)2 – (9)2
= (4x2 + 9)(4x2 – 9)
= (4x2 + 9)[(2x)2 – (3)2]
= (4x2 + 9)(2x + 3) (2x – 3)
(b) (a – b)2 + 4ab
= a2 – 2ab + b2 + 4ab
= a2 + 2ab + b2
= (a + b)2
Q10: Factorise:
(а) 14m5n4p2 – 42m7n3p7 – 70m6n4p3
(b) 2a2(b2 – c2) + b2(2c2 – 2a2) + 2c2(a2 – b2)
Ans:
(a) 14m5n4p2 – 42m7n3p7 – 70m6n4p3
= 14m5n3p2(n – 3m2p5 – 5mnp)
(b) 2a2(b2 – c2) + b2(2c2 – 2a2) + 2c2(a2 – b2)
= 2a2(b2 – c2) + 2b2(c2 – a2) + 2c2(a2 – b2)
= 2[a2(b2 – c2) + b2(c2 – a2) + c2(a2 – b2)]
= 2 × 0
= 0
Q11: Factorise:
(a) (x + y)2 – 4xy – 9z2
(b) 25x2 – 4y2 + 28yz – 49z2
Ans:
(a) (x + y)2 – 4xy – 9z2
= x2 + 2xy + y2 – 4xy – 9z2
= (x2 – 2xy + y2) – 9z2
= (x – y)2 – (3z)2
= (x – y + 3z) (x – y – 3z)
(b) 25x2 – 4y2 + 28yz – 49z2
= 25x2 – (4y2 – 28yz + 49z2)
= (5x)2 – (2y – 7)2
= (5x + 2y – 7) [5x – (2y – 7)]
= (5x + 2y – 7) (5x – 2y + 7)
|
79 videos|408 docs|31 tests
|
FAQs on Class 8 Maths - Factorisation CBSE Worksheets Solutions
| 1. What is factorisation? |  |
| 2. How can I factorise a quadratic expression? |  |
| 3. What are the common methods of factorisation? |  |
| 4. Can factorisation help in solving equations? |  |
| 5. What are the applications of factorisation in real life? |  |

|
Explore Courses for Class 8 exam
|

|

















