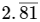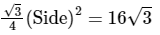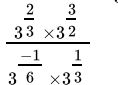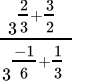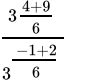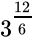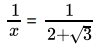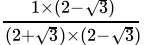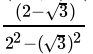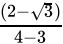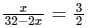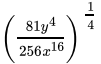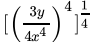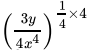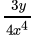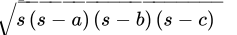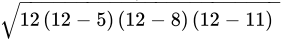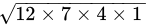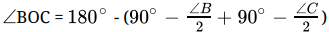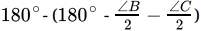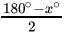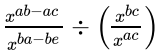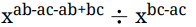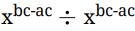Class 9 Math: Sample Question Paper Term I- 2 (With Solutions) | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Class 09 Mathematics |

|
| Time: 90 Minutes |

|
| Max. Marks: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class 09 Mathematics
Time: 90 Minutes
Max. Marks: 40
General Instructions :
- The question paper contains three parts A, B and C
- Section A consists of 20 questions of 1 mark each. Attempt any 16 questions
- Section B consists of 20 questions of 1 mark each. Attempt any 16 questions.
- Section C consists of 10 questions based on two Case Studies. Attempt any 8 questions.
- There is no negative marking.
Section - A
Q.1: The value of  is
is
(a) 31/11
(b) 24/11
(c) 67/33
(d) 167/110
Correct Answer is Option (a)
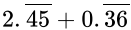
=
= 279/99
= 31/11
Q.2: If a linear equation has solutions (-1, 1 ), (0, 0), (2, -2), then its equation is
(a) y - x = 0
(b) x + y = 0
(c) -2x + y = 0
(d) -x + 2y= 0
Correct Answer is Option (b)
Out of all the options, (-1, 1 ), (0, 0), (2, -2) are the solutions of x + y = 0 only.
Q.3: In Fig. if l1 || l2 and l3 || l4, what is y in the terms of x?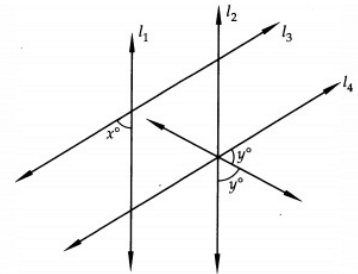
(a) 90 + 2x
(b) 90 - x/2
(c) 90 – 2x
(d) 90 + x
Correct Answer is Option (b)
Given that,
l1 ‖ l2 and l3 ‖ l4
Let,
∠1 = x
∠2 = y
∠3 = y
∠1 = ∠4 (Alternate angle)
∠4 = x
∠5 = ∠2 (Vertically opposite angle)
∠6 = ∠3 (Vertically opposite angle)
∠5 = ∠6 = y
Now,
∠4 + ∠5 + ∠6 = 180o (Consecutive interior angle)
y = 90 - x/2
Q.4: If the area of an equilateral triangle is 16√3cm2, then the perimeter of the triangle is
(a) 36 cm
(b) 48 cm
(c) 24 cm
(d) 12 cm
Correct Answer is Option (c)
Area of equilateral triangle =
⇒ (Side)2 = 64
⇒ Side = 8 cm
Perimeter of equilateral triangle = 3 x side
= 3 x 8 = 24 cm
Q.5: √12 x √15 = ?
(a) 5
(b) 5√6
(c) 6√5
(d) 6
Correct Answer is Option (c)
√12 == 2√3 and √15 = √5 x √3
So, √12 x √15 = 2√3 x √3 x √5
= 2 x 3√5 = 6√5
Q.6: The graph of the equation x + y = 4
(a) intersects y-axis only
(b) parallel to x-axis
(c) intersects both the axis
(d) intersects x-axis only
Correct Answer is Option (c)
The graph of the equation x + y = 4
Put x=0 cut y axis at y = 4
Put y=0 cut x axis at x = 4
Q.7: A point of the form (a, 0) lies on
(a) quadrant I
(b) x- axis
(c) quadrant IV
(d) y- axis
Correct Answer is Option (b)
The given point of the form = (a, 0)
Here, x-co-ordinate = a and y-co-ordinate = 0
∴ The point of the form (a, 0) always lies on x-axis.
Thus, the point of the form (a, 0) always lies on x-axis.
Q.8: ΔABC ≅ ΔPQR, then which of the following is true?
(a) CA = RP
(b) CB = QP
(c) AB = RP
(d) AC = RQ
Correct Answer is Option (a)
Corresponding sides are equal for two congruent triangles.
Q.9: Choose the rational number which does not lie between -2/3 and -1/5
(a) -7/20
(b) -3/10
(c) -1/4
(d) 3/10
Correct Answer is Option (d)
3/10 > -2/3 and 3/10 > -1/5
Q.10: In ΔABC and ΔDEF it is given that AB = DE and BC = EF in order that ΔABC ≅ ΔDEF, we must have
(a) ∠C = ∠F
(b) ∠A = ∠D
(c) ∠B = ∠E
(d) None of these
Correct Answer is Option (c)
Given, AB = DE and BC = EF
For ∠B = ∠E
ABC ≅ ΔDEF
Q.11: In the given figure, AOB is a straight line. If ∠AOC = 4x° and ∠BOC = 6x° then ∠AOC =?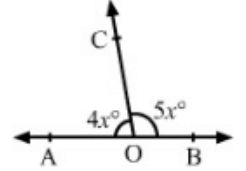
(a) 60°
(b) 40°
(c) 100°
(d) 80°
Correct Answer is Option (d)
∠AOC + ∠BOC = 180° [Since AOB is a straight line]
⇒ 4x + 5x = 180°
⇒ 9x = 180°
⇒ x = 20°
∴ ∠AOC = 4 x 20° = 80°
Q.12: The value of 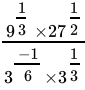 is
is
(a) 27
(b) 9
(c) 1
(d) 3
Correct Answer is Option (b)
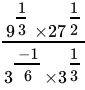
⇒
⇒
⇒
⇒
⇒
= 9
Q.13: The product of a nonzero rational number with an irrational number is always a/an
(a) irrational number
(b) whole number
(c) natural number
(d) rational number
Correct Answer is Option (a)
The product of a non-zero rational number with an irrational number is always an irrational number.
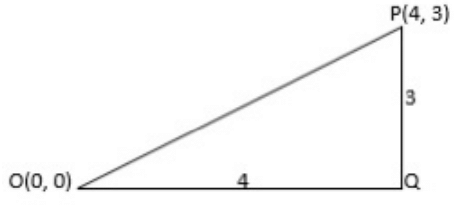
Q.14: The distance of the point P (4, 3) from the origin is
(a) 3
(b) 5
(c) 7
(d) 4
Correct Answer is Option (b)
Using Pythagorous theorem: OP2 = OQ2 + QP2
OP2 = 42 + 32OP2 = √16 + 9 = 5
Q.15: The graph of y = 4x will
(a) pass through the origin
(b) none of these
(c) intersect x-axis
(d) intersect y-axis
Correct Answer is Option (a)
The graph of y = 4x will pass through the origin (0,0)
y = 4x
at x = 0
y = 4.0
y = 0
so the graph y = 4x will pass from point (0,0)
Q.16: Find the measure of each exterior angle of an equilateral triangle.
(a) 110o
(b) 100o
(c) 150o
(d) 120o
Correct Answer is Option (d)
We know that in equilateral triangle each angle is 60o
and we know sum of interior angle and exterior angle is 180o
let exterior angle be x
60o + x = 180o
x = 180o - 60o
x = 120o
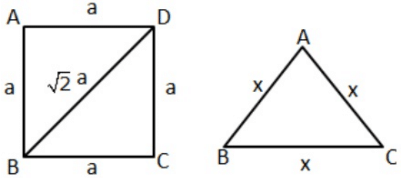
Q.17: A square and an equilateral triangle have equal perimeters. If the diagonal of the square is 12√2 cm, then area of the triangle is
(a) 24√2 cm2
(b) 64√3 cm2
(c) 24√3 cm2
(d) 48√3 cm2
Correct Answer is Option (b)
If side of a square is a cm then, its diagonal = √2a cm
But diagonal = 12 √2 cm
⇒ √2a = 12 √2
⇒ a = 12 cm
⇒ Perimeter of a square = 4a = 4 12= 48cm
Now, perimeter of an equilateral triangle with side x = 3x cm
But, perimeter of equilateral triangle = Perimeter of square
⇒ 3x = 48
⇒ x = 16 cm
Now, Area of equilateral Δ == 64√3 cm2
Q.18: ‘More than’ cumulative frequency table for a given data is as follows: Then, the frequency of the class interval 70-80 is
(a) 12
(b) 10
(c) 22
(d) 35
Correct Answer is Option (a)
A cumulative frequency distribution is the sum of the class and all classes below it in a frequency distribution.
Subtract cumulative frequency of class more than 70 from the next cummulative Frequency of class more than 69.
30-18 = 12
Q.19: if a = 2 + √3, then the value of 1/a is
(a) 2 + √3
(b) √3 - 2
(c) 1
(d) 2 - √3
Correct Answer is Option (d)
x = 2 + √3
=
=
=
= 2 - √3
Q.20: The point which lies on y-axis at a distance of 10 units in the negative direction of y-axis is
(a) (10, 0)
(b) (0, 10)
(c) (0, -10)
(d) (-10, 0)
Correct Answer is Option (c)
(0, -10)
Section - B
Q.21: Any solution of the linear equation 2x + 0y + 9 = 0 in two variables is of the form
(a) 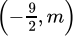
(b) (-9 , 0)
(c) 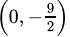
(d) 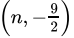
Correct Answer is Option (a)
2x + 9 = 0
⇒ x = 9/2 and y = m, where m is any real number
Hence,is the solution of the given equation.
Q.22: The perimeter of an isosceles triangle is 32 cm. the ratio of the equal side to its base is 3 : 2. Then area of the triangle is
(a) 32 cm2
(b) 32√2 cm2
(c) 16√2 cm2
(d) 16 cm2
Correct Answer is Option (b)
Let each of the equal sides of given triangle be x cm. Then the third side is (32 - 2x) cmAccording to question,
⇒ 2x = 96 - 6x
⇒ 8x = 96
⇒ x = 12 cm
Therefore, the sides are 12 cm, 12 cm and 8 cm
Q.23: Express ‘x’ in terms of ‘y’ in the equation 2x – 3y – 5 = 0.
(a) 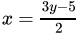
(b) 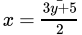
(c) 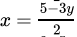
(d) 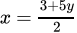
Correct Answer is Option (b)
2x – 3y – 5 = 0
2x = 3y + 5
x= 3y + 5 / 2
Q.24: If one of the angles of a triangle is 130, then the angle between the exterior bisectors of the other two angles is given by:
(a) 59°
(b) 155°
(c) 90°
(d) 118°
Correct Answer is Option (b)
Let ∠A, ∠B,∠C are three angles in a triangle.
Sum of the three angles in a triangle is .
∠A + ∠B + ∠C = 180
130 + ∠B + ∠C = 180 ...Since one angle is given
∠B + ∠C = 180 - 130
∠B + ∠C = 50
(∠B + ∠C /2) = 25 ...(1) After bisecting sum of the angles
Q.25: The value of 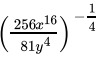 is
is
(a) 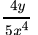
(b) 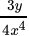
(c) 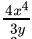
(d) 
Correct Answer is Option (b)
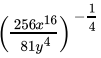
=
=
=
=
=
Q.26: Length of perpendicular drawn on longest side of a scale Δ is
(a) largest
(b) smallest
(c) No relation
(d) Equal
Correct Answer is Option (b)
Length of the perpendicular drawn on the longest side of a scale is Δ smallest.
Q.27: Mode is
(a) middle most value
(b) most frequent value
(c) least frequent value
(d) none of these
Correct Answer is Option (b)
We know that, mode is the observation which occur maximum number of times.
Q.28: 0.83458456…………… is
(a) a natural number
(b) an irrational number
(c) rational number
(d) a whole number.
Correct Answer is Option (b)
Some numbers cannot be written as a ratio of two integers they are called Irrational Numbers.
It is irrational because it cannot be written as a ratio (or fraction),
Q.29: The sum of the angles of a triangle is
(a) 90o
(b) 180o
(c) 360o
(d) 0o
Correct Answer is Option (b)
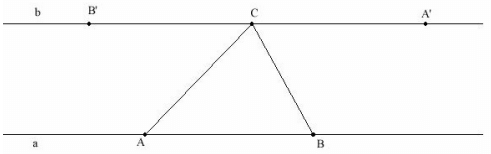
Line a and b are parallel.
∠B'CA = ∠BAC (Alternate interior angle)
∠A'CB = ∠ABC (Alternate interior angle)
∠B'CA + A'CB + ∠BCA = 180o (Linear Pair)
Therefore, ∠BAC + ∠ABC + ∠BCA = 180o
Q.30: The mean of X1, X2, ......., Xn is 10, then the mean of 5x1, 5x2, .........5Xn is
(a) 15
(b) 50
(c) 10
(d) 5
Correct Answer is Option (b)
We know that if every observation is multiplied by a constant, then their arithmetic mean is also multiplied by the same constant.
Q.31: The sides of a triangular flower bed are 5 m, 8 m and 11 m. the area of the flower bed is
(a) 21√4 m2
(b) 4√21 m2
(c) √300 m2
(d) √330 m2
Correct Answer is Option (b)
s == 12m
Area of triangle =
=
=
= 4√21 sq.m
Q.32: The number 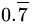 in the form p/q, where p and q are integers and q ≠ 0, is
in the form p/q, where p and q are integers and q ≠ 0, is
(a) 77/10
(b) 7/10
(c) 7/100
(d) 7/9
Correct Answer is Option (d)
Let x = 0.777... ----(i)
multiply both side by 10, we get
10 x = 7.777... -----(ii)
subtracting (i) from (ii), we get,
10x- x = 7.777.... - 0.777...
⇒ 9x = 7
∴ x = 7/9
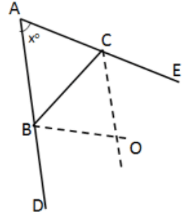
Q.33: The bisector of exterior angles at B and C of ΔABC meet at O. If ∠A = x°, then BOC =
(a) 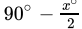
(b) 
(c) 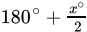
(d) 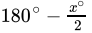
Correct Answer is Option (a)
In ΔABC
∠A + ∠B + ∠C = 180o
∠B + ∠C = 180o - xo ...(i)
∠CBD = 180o - ∠B ...(ii)
∠ECB = 180o - ∠C ...(iii)
⇒...(iv) [From eq (ii)]
...(v) [From eq (iii)]
Now, in ΔBOC
∠OBC + ∠OCB + ∠BOC = 180o
∠BOC = 180o - (∠OBC + ∠OCB)
From eq (iv) and (v)
=
=[from eq (i)]
=
∠BOC =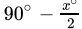
Q.34: A data is such that its maximum value is 75 and range is 20, then the minimum value is
(a) 95
(b) 20
(c) 75
(d) 55
Correct Answer is Option (d)
Difference between the maximum and minimum value of the observations is called as range.
Let, minimum value be 'x'
75 - x = 20
So, x = 55
Q.35: Two straight lines AB and CD cut each other at O. If ∠BOD = 63°, then ∠BOC=(a) 117°
(b) 17°
(c) 153°
(d) 63°
Correct Answer is Option (a)
∠BOD + ∠BOC = 180o (Linear pair)
63o + ∠BOC = 180o
∠BOC = 117o
Q.36: The graph of the linear equation 2x + 3y = 6 meets the y-axis at the point.
(a) (0, 2)
(b) (2, 0)
(c) (3, 0)
(d) (0, 3)
Correct Answer is Option (a)
If the graph of the linear equation 2x + 3y = 6 meets the y-axis, then x = 0.
Substituting the value of x = 0 in equation 2x + 3y = 6, we get
2(0) + 3y = 6
⇒ 3y = 6
⇒ y = 6/3
⇒ y = 2
So, the point of meeting is (0, 2).
Q.37: For any ΔABC, AB + BC is always:
(a) None of these
(b) Greater than AC
(c) Less than AC
(d) Equal to AC
Correct Answer is Option (b)
Sum of any two sides is greater than third side.
Q.38: The value of 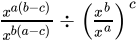 is
is
(a) 1
(b) 3
(c) 4
(d) 2
Correct Answer is Option (a)
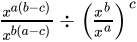
⇒
⇒
⇒
⇒ 1
Q.39: The range of the data 12, 25, 15, 18, 17, 20, 22, 6, 16, 11, 8, 19, 10, 30, 20, 32 is
(a) 26
(b) 16
(c) 18
(d) 15
Correct Answer is Option (a)
Difference between the maximum & minimum value of the observation is called as range.
So, 32 - 6 = 26
Q.40: A student collects information about the number of school going children in a locality consisting of a hundred households. The data collected by him is
(a) Arrayed data
(b) Grouped data
(c) Primary data
(d) Secondary data
Correct Answer is Option (c)
Data obtained through the information collected by the investigator herself or himself with definite objective in his/her mind is called as primary data.
Section - C
Question No. 41 to 45 are based on the given text. Read the text carefully and answer the questions:
Four friends decided to play a game, Meena advised instead of playing physical game let's play a geometry game.
Meena Drew a ΔABC. Rohit found the midpoint of side AB and marked it as D. Now the third student Mathew, from D drew a line DE||BC, for this, he made ∠ADE = ∠ABC.
Further, the fourth friend Veena from the point E drew a line parallel to AB, She observed that this line cuts Bc at New point F. Veena found that EF = BD. As marked in the given picture.
Now all the friends were trying to prove that ΔADE ≅ ΔEFC.
Q.41: In the ΔADE and ΔEFC, AD =?
(a) CE
(b) EF
(c) AE
(d) FC
Correct Answer is Option (b)
EF
Q.42: In the ΔADE and ΔEFC, ∠1 =?
(a) ∠q
(b) ∠r
(c) ∠A
(d) ∠E
Correct Answer is Option (a)
∠q
Q.43: In the ΔADE and ΔEFC, ∠2 =?
(a) ∠r
(b) ∠A
(c) ∠q
(d) ∠E
Correct Answer is Option (a)
∠r
Q.44: ΔADE and ΔEFC are congruent according to which criteria:
(a) SAS
(b) ASA
(c) SSS
(d) RHS
Correct Answer is Option (b)
ASA
Q.45: AE is equal to which side?
(a) BD
(b) EC
(c) DE
(d) AD
Correct Answer is Option (b)
EC
Question No. 46 to 50 are based on the given text. Read the text carefully and answer the questions: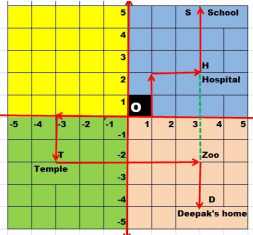 In the above picture, one small square is of size 1 km X 1 km. From the starting point O(0,0) Deepak started to drive towards his home. He first drives 3km in left then he turned to his left and drove 2 km, there he found a temple. He worshipped there and drove 6km in the left direction, there is a zoo and from the zoo, he drives 2km on the right side, then he reached his home.
In the above picture, one small square is of size 1 km X 1 km. From the starting point O(0,0) Deepak started to drive towards his home. He first drives 3km in left then he turned to his left and drove 2 km, there he found a temple. He worshipped there and drove 6km in the left direction, there is a zoo and from the zoo, he drives 2km on the right side, then he reached his home.
From O Sanjay drove for his school, he drove 1km to his right then took a left turn and drives 2km then again took a right turn and drives 2 km. He found a hospital in the way. From Hospital he drove 3 km and finally reached his school.
Q.46: What are the coordinates of the Hospital?
(a) (2, 3)
(b) (5, 5)
(c) (3, 2)
(d) (3, 3)
Correct Answer is Option (c)
(3, 2)
Q.47: What is common abscissa of school, Hospital, Zoo and Deepak's home?
(a) 3
(b) 5
(c) -3
(d) -5
Correct Answer is Option (a)
3
Q.48: What is the common ordinate of temple and Zoo?
(a) 5
(b) -2
(c) -3
(d) 3
Correct Answer is Option (b)
-2
Q.49: Deepak Drove in which quadrants?
(a) IV and I
(b) III and IV
(c) II and III
(d) I and II
Correct Answer is Option (b)
III and IV
Q.50: Sanjay Drove in which quadrants?
(a) I only
(b) II and I
(c) III and IV
(d) II and III
Correct Answer is Option (a)
I only
|
40 videos|470 docs|56 tests
|