Class 9 Maths Chapter 1 Practice Question Answers - Number System
Q1: The decimal expansion of π is :
(a) terminating
(b) non-terminating and non-recurring
(c) non-terminating and recurring
(d) doesnt exist
 View Answer
View Answer 
Ans: (b)
We know that π is irrational number and Irrational numbers have decimal expansions that neither terminate nor become periodic.
So, correct answer is option B.
Q2: A number is an irrational if and only if its decimal representation is:
(a) non terminating
(b) non terminating and repeating
(c) non terminating and non repeating
(d) terminating
 View Answer
View Answer 
Ans: (c)
According to definition of irrational number, If written in decimal notation, an irrational number would have an infinite number of digits to the right of the decimal point, without recurring digits.
Hence, a number having non terminating and non repeating decimal representation is an irrational number.
So, option C is correct.
Q3: Between any two rational numbers,
(a) there is no rational number
(b) there is exactly one rational number
(c) there are infinitely many rational numbers
(d) there are only rational numbers and no irrational numbers
 View Answer
View Answer 
Ans: (c)
Recall that to find a rational number between r and s, you can add r and s and divide the sum by 2, that is (r+s)/2 lies between r and s.
For example, 5/2 is a number between 2 and 3.
We can proceed in this manner to find many more rational numbers between 2 and 3.
Hence, we can conclude that there are infinitely many rational numbers between any two given rational numbers.
Q4: Every rational number is
(a) A natural number
(b) An integer
(c) A real number
(d) A whole number
 View Answer
View Answer 
Ans: (c)
Every rational number is a number that can be expressed in the form , where and are integers and . Rational numbers are a subset of real numbers, but not all rational numbers are natural, integers, or whole numbers.
Q5: The product of a non - zero rational number with an irrational number is always :
(a) Irrational number
(b) Rational number
(c) Whole number
(d) Natural number
 View Answer
View Answer 
Ans: (a)
The product of a non-zero rational number with an irrational number is always irrational. This is because multiplying a rational number with an irrational number does not eliminate the non-repeating, non-terminating nature of the irrational number. For example, 2 x √2 = 2√2 which is irrational.
Q6: Which of the following numbers are rational ?
(a) 1
(b) -6
(c) 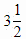
(d) All above are rational
 View Answer
View Answer 
Ans: (d)
⇒ A rational number is a type of real numbers which can be expressed in the form of p/q , where q ≠ 0.
⇒ All the numbers are rational as they are in the form of p/q , where q ≠ 0.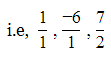
Q7: Find the decimal expansions of 10/3, 7/8 and 1/7.
 View Answer
View Answer 
Ans: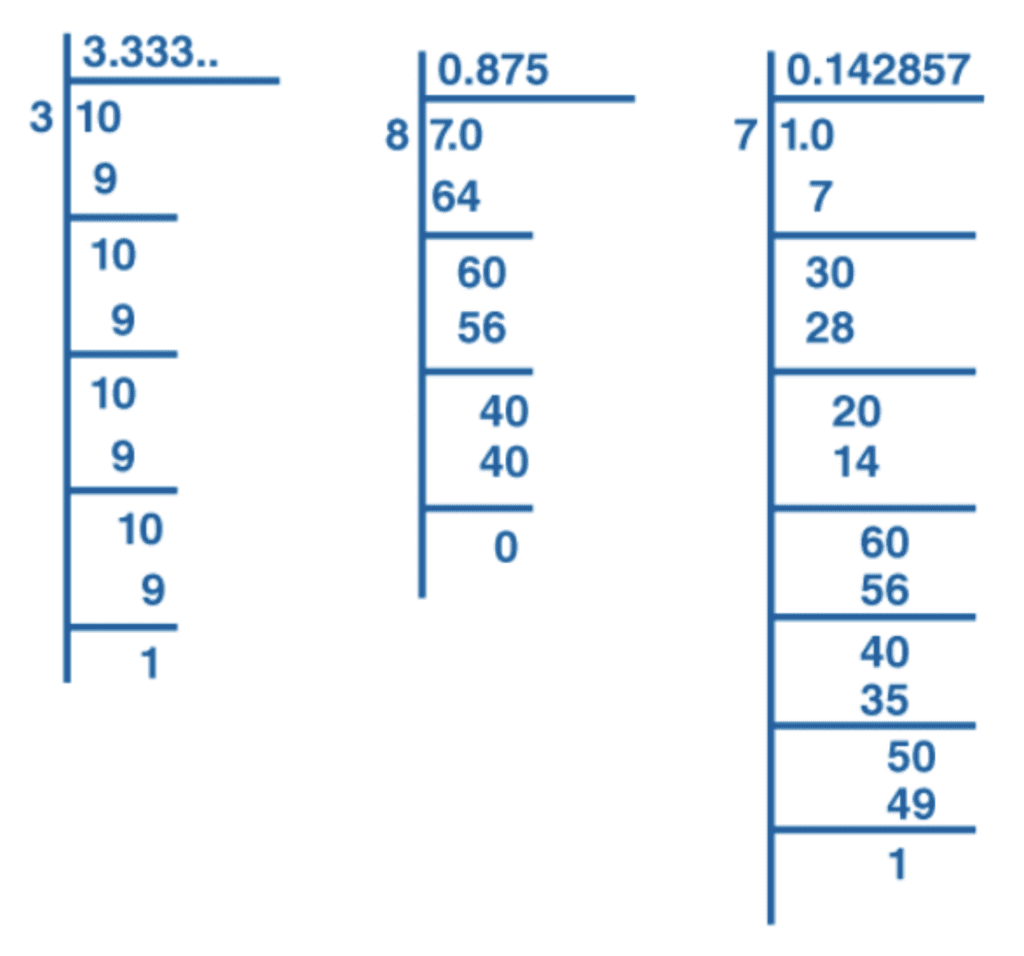
Therefore, 10/3 = 3.3333…
7/8 = 0.875
1/7 = 0.1428571…
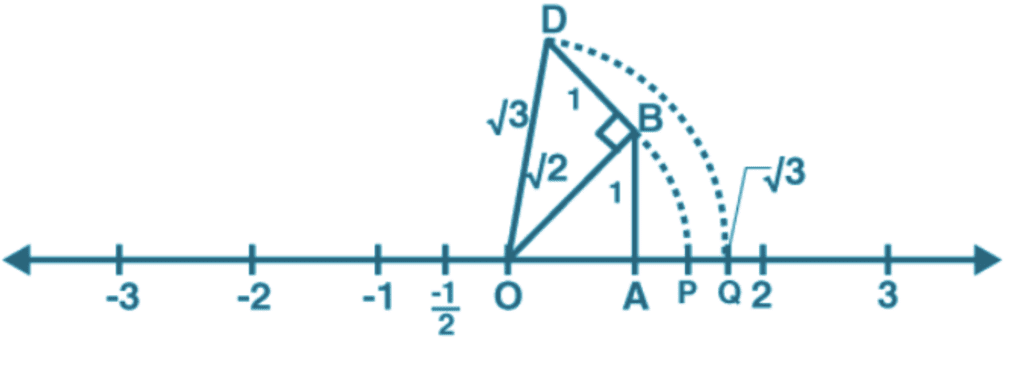
Q8: Locate √3 on the number line.
 View Answer
View Answer 
Ans: Construct BD of unit length perpendicular to OB (here, OA = AB = 1 unit) as shown in the figure.
By Pythagoras theorem,
OD = √(2 + 1) = √3
Taking O as the centre and OD as radius, draw an arc which intersects the number line at the point Q using a compass.
Therefore, Q corresponds to the value of √3 on the number line.
Q9: Identify whether the given number is a rational or irrational number: √12√75
 View Answer
View Answer 
Ans:
Given,
√12√75
= √(2 × 2 × 3)√(3 × 5 × 5)
= 2√35√3
= 25
Here, both 2 and 5 are integer.
Therefore, √12√75 is a rational number.
Q10: Simplify: (√3+√7) (√3-√7).
 View Answer
View Answer 
Ans: (√3 + √7)(√3 – √7)
Using the identity (a + b)(a – b) = a2 – b2,
(√3 + √7)(√3 – √7) = (√3)2 – (√7)2
= 3 – 7
= -4
Q11: When denominator is rationalised, then the number 5 + 2√37 + 4√3 becomes a−6√3. Find the value of
 View Answer
View Answer 
Ans: We need to rationalise
5 + 2√37 + 4√3
= (5 + 2√3)(7 + 4√3) × (7 - 4√3)(7 - 4√3)
= (5 + 2√3)(7 - 4√3)49 - 48
= (35 - 20√3 + 14√3 - 24)
= 11 - 6√3
Now comparing this with a−6√3 , we get
a = 11
Q12: Which of the following is irrational number?
(a) √ 818
(b) √ 123
(c) √ 288
(d) √81
 View Answer
View Answer 
Ans: (c)
All numbers that can be written in the form of p/q , where p and q are integers are rational numbers.
Option A:
√ 818 = √ 49 = 23
Hence, it is rational.
Option B:
√ 123 = √4 = 2
Hence, it is a rational number.
Option C:
√ 288 = √ 72
This cannot be simplified further.
This is an irrational number.
Option D:
√81 = 9
This is a rational number.
Hence, option C is correct.
Q13: Simplify:
(i) 72/3 . 71/5
(ii) 101/2 / 101/4
 View Answer
View Answer 
Ans: (i) 72/3.71/5
Bases are equal, so add the powers.
7(2/3 + 1/5)
= 7(10 + 3)/15
= 713/15
(ii) 101/2/101/4
Bases are equal, so subtract the powers.
= 10 (1/2 – 1/4)
= 101/4
Q14: What is the value of (256)0.16 X (256)0.09?
a) 4
b) 16
c) 64
d) 256.25
 View Answer
View Answer 
Ans: (a)
(256)0.16 x (256)0.09 = (256)(0.16 + 0.09)
= (256)0.25
= (256)(25/100)
= (256)(1/4)
= (44)(1/4)
= 44(1/4)
= 4
Q15: The value of 1.999... in the form p/q, where p and q are integers and q ≠ 0, is
(a) 1/9
(b) 19/10
(c) 1999/1000
(d) 2
 View Answer
View Answer 
Ans: (d)
Consider x = 1.999 …. (1)
Let us multiply equation (1) with 10
10x = 19.99 …. (2)
Subtracting equation (1) from (2)
9x = 18
Dividing both sides by 9
x = 2
Therefore, the value of 1.999... is 2.
Hence, option D is correct answer.
Q16: Two rational numbers between 1/5 and 4/5 are:
(a) 1 and 3/5
(b) 2/5 and 3/5
(c) 1/2 and 2/1
(d) 3/5 and 6/5
 View Answer
View Answer 
Ans: (b)
Since the denominator of both rational numbers are same. So, for getting the rational numbers between the given rational numbers, we only have to consider the numerators of the rational numbers.
Two numbers between 1 & 4 are 2 and 3.
So, two rational numbers between the given rational numbers will be 2/5 and 3/5
So, correct answer is option B.
Q17: π is a/an _______ .
(a) Rational number
(b) Integer
(c) Irrational number
(d) Whole number
 View Answer
View Answer 
Ans: (c)
The value of π is equal to 3.14159265358… which is a non-terminating and non-repeating decimal hence, π is an irrational number.
Q18: Why is 0.111222333444..., where each number appears 3 times in a row irrational?
 View Answer
View Answer 
Ans: Since in 0.111222333444.... each number appears 3 times in a row is a non- terminating and non- recurring decimal expansion.
Hence, 0.111222333444.... is irrational.
Q19: If x = √2 +1. Find the value of 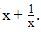
 View Answer
View Answer 
Ans:
Given: x = √2 + 1
∴ 1x = 1√2 + 1
= √2 - 1(√2)2 - 12 {Using method of Rationalisation}
= √2 - 12 - 1 = √2 - 1
∴ x + 1x = (√2 + 1 + √2 - 1) = 2√2
Q20: Find five rational numbers between 3/5 and 4/5.
 View Answer
View Answer 
Sol: We have to find five rational numbers between 3/5 and 4/5.
So, let us write the given numbers by multiplying with 6/6, (here 6 = 5 + 1)
Now,
3/5 = (3/5) × (6/6) = 18/30
4/5 = (4/5) × (6/6) = 24/30
Thus, the required five rational numbers will be: 19/30, 20/30, 21/30, 22/30, 23/30
|
40 videos|566 docs|57 tests
|
FAQs on Class 9 Maths Chapter 1 Practice Question Answers - Number System
| 1. What are the different types of number systems used in mathematics? |  |
| 2. How do you convert a decimal number to a binary number? |  |
| 3. What is the difference between rational and irrational numbers? |  |
| 4. How do you perform arithmetic operations in different number systems? |  |
| 5. What role do number systems play in computer science? |  |






















