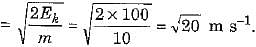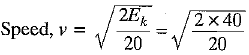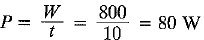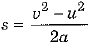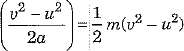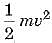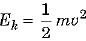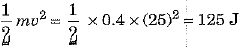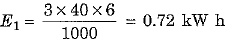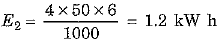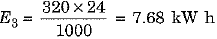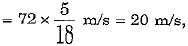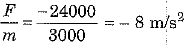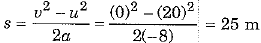Short Answer Type Questions
Q.1. A truck of mass 1800 kg is moving with a speed 54 km/h. When brakes are applied, it stops with uniform negative acceleration at a distance of 200 m. Calculate the force applied by the brakes of the truck and the work done before stopping. [2023]
Ans: Given: Mass, m = 1800 kg; Velocity,
u = 54 km/h = 
m/s = 15 m/s; v = 0;
Distance, 5 = 200 m
Retardation, a
=
Force, F = ma = 1800 x
= -1012.5 N
The negative sign indicates force acts in the opposite direction to motion.
Work done = Fs = 1012.5 x 200
= 202500 J
Q.2. Define power. [ 2023]
Ans: The rate of doing work or the rate of transfer of energy is known as the power.
∴
Q.3. State the law of conservation of energy. [2023]
Ans: Energy can neither be created nor be destroyed. It can only be transformed from one form to another.
Illustration of Law of Conservation of Energy
Q.4. State the type of transformation of energy during ‘burning of a cracker’. [2022]
Ans: During burning of a cracker chemical energy is being transformed in the form of light and sound energy.
Q.5. Why the energy of an object is increased when raised through a height? [2021]
Ans: When an object is raised through a height, work: is done against its weight (i.e., against the force of gravity). This work done is stored in the form of its potential energy due to which energy of object increases.
Q.6. (a) Define kinetic energy.
(b) The masses of scooters and bikes are in the ratio of 2 :3, but both are moving with the same speed of 108 km/h. Compute the ratio of their kinetic energy. [2021]
Ans: (a) The energy possessed by a body by virtue of its motion is called kinetic energy.
(b) Kinetic energy ∝ Mass of body
Let mass of scooter = ms - 2m
and mass of bike = mb = 3m
∴
Q.7. A labourer whose own mass is 50 kg carries a lo ad of an additional 60 kg on his head to the top of a building 15 m high. Find the total work done by him. Also, find the work done by him if he carries another additional block of mass 10 kg to the same height. (Take g = 10 m/s2) [2020]
Ans: Here mass of labourer m1 = 50 kg, mass of load carried by him m2 = 60 kg and height of the building h = 15 m.
∴ Total force applied by labourer F = (m1 + m2)g
Work done W = Fs = (m1 + m2)gh = (50 + 60) x 10 x 15 = 16500 J
When the labourer carries an additional load of mass m3 = 10 kg, total force
F' = (m1 + m2 + m3)g
Total work done W' - F's = (m1 + m2 + m3)gh
= (50 + 60 + 10) x 10 x 15 = 18000 J
Q.8. What is the work to be done to increase the velocity of a car from 36 km h-1 to 72 km h-1 if the mass of car is 1500 kg? [2020]
Ans: Here mass of the car m - 1500 kg, initial velocity of car u = 36 km h-1 =
= 10 m s-1 and final velocity of car v = 72 km h-1
= Work to be done on the car - Increase in K.E. of car
⇒
Q.9. A body of mass 3 kg is thrown vertically upwards with an initial velocity of 20 m/s. What will be its potential energy at the end of 2 s? (Take g = 10 m/s-2) [2020]
Ans: Here mass of body m = 3 kg, initial upward velocity u = 20 m/s, g = 10 m/s2
After a time t = 2 s, the body is at a height h, where
∴ Potential energy of body at t = 2 s, Ep = mgh = 3 x 10 x 20 = 600 J
Q.10. A car is moving on a levelled road and gets its velocity doubled. In this process:
(а) how would the potential energy of the car change?
(b) how would the kinetic energy of the car change?
(c) how will its momentum change?
Give reasons for your answer. [2020]
Ans: (a) The potential energy remains unchanged as the car is moving on a levelled road such that its height 'h' above the ground does not change and potential energy Ep = mgh remains unchanged.
(b) When velocity of car is doubled v'/ = 2v) then its kinetic energy Ek increases to 4 times of its initial kinetic energy Ek as shown below :
(c) Momentum 'p' of car is given as : p = mv. When velocity of the car is doubled, its momentum is also accordingly doubled to p' = 2p
p' = mv' - m(2v) = 2mv - 2p
Q.11. (a) Water is falling on the blades of a turbine at the rate of 6 x 103 kg per minute. The height of the fall is 10 m. Calculate the power given to the turbine.
(Take g = 10 m/s2)
(b) A driver speeds up his vehicle when he moves up a hill. Give reason. [2019]
Ans: (a) Here mass of water falling on the blades of a turbine m = 6 x 103 kg, time t = 1 minute = 60 s, height of the fall h = 10 m and g = 10 m/s2
∴ Energy supplied to turbine = Loss in potential energy of water = mgh
∴
(b) When a driver moves his vehicle up a hill, the force of gravity opposes his motion and he needs greater power. For this purpose, the driver speeds up his vehicle.
Q.12. A lamp consumes 500 J of electrical energy in 20 seconds. What is the power of the lamp? Also, find the electrical energy consumed in units if the lamp operates for 2 hours daily for 15 days. [2019]
Ans: Here energy consumed E = 500 J and time t = 20 s
∴ Power of the lamp P =
Further electrical energy consumed by the lamp in operation for t = 2 hours daily for n = 15 days is
Q.13. Define one-kilowatt hour (1 kW h). [2019]
Ans: Energy consumed is said to be one-kilowatt hour (1 kW h) if energy is being used at a rate of 1 kW (or 1000 J per second) for a time of 1 hour.
Q.14. State the value of commercial units of energy in joules.
Or
State the relation between kW h and joule. [2019]
Ans: 1 kW h = 3.6 x 106 J.
Q.15. A body of mass 100 g is lifted to a height of 10 m. Find (i) the amount of work done, (ii) the potential energy of the body at that height. (Take g = 10 m s-2) [2018]
Ans: Here mass of body m = 100 g = 0.1 kg, height h =i 10 m and g = 10 m s-2.
(i) ∴ Work was done on the body against the force of gravity.
W = Fs = mg x h - 0.1 x 10 x 10 - 10 J
(ii) The potential energy of the body Ep = mgh = 0.1 x 10 x 10 = 10 J.
Q.16. Define power. State commercial unit and SI unit of electrical energy. An electric heater of 400 W works for 2 hours. Find the electrical energy units consumed in a day. [2018]
Ans: Power of a device is defined as work done by it per unit time.
Commercial unit of energy: kilowatt-hour (kWh)
SI unit of energy: joule (J)
Given: power, P = 400 W = 0.4 kW;
Time, t = 2 h
Energy unit consumed in a day = Pt
= 0.4 kW x 2 h = 0.8 kWh
Q.17. State two factors on which the magnitude of gravitational potential energy depends. [2018]
Ans: Magnitude of gravitational potential energy of an object depends on
(i) its mass, and (ii) its height above the ground level.
Q.18. Distinguish between positive work and negative work. When you lift an object up, two forces act on it. Identify these forces. Which one of the two does:
(a) Positive work
(b) Negative work?
Justify your answer. [2018]
Ans: Work done is said to be positive if the displacement of the object is along the direction of force applied. On the other hand, work is said to be negative if the displacement of the object is in a direction opposite to the direction of force applied.
When a person lifts an object up, two forces are acting on the object.
These are :
(i) Force due to gravity F - mg, where m = mass of the object and g = acceleration due to gravity. The force acts in vertically downward direction.
(ii) A force F applied by the person whose magnitude is equal to F but direction is opposite. Thus, F' = F = mg acts in vertically upward direction.
Out of these two forces (a), the force F applied by the person does positive work because the displacement of object in upward direction is along the direction of force F. (b) The force of gravity F = mg does negative work because the force F - mg acts in vertically downward direction and displacement is upward.
Q.19. An object of mass 10 kg is dropped from a height of 100 cm. Find its :
(a) kinetic energy
(b ) velocity, just as it reaches the ground, (g = 10 m/s2) [2017]
Ans: Here mass of object m = 10 kg, height from which dropped h = 100 cm = 1 m and g = 10 m s-2.
(a) K.E. of obiect on reaching ground Ek = = Gravitational potential energy before falling = msh = 10 x 10 x 1 = 100J
(b) ∵ , hence velocity v =
Q.20. In a factory 10 bulbs of 50 W, each and 5 fans of 70 W each operate for 12 hours daily. Calculate the units of electricity consumed. Also, find the expenditure if 1 unit costs Rs 2. [2017]
Ans: Here energy consumed in a factory for running 10 bulbs of 50 W each when used for 12 hours
E1 - 10 x 50 x 12 = 6000 W h = 6.0 kW h
and energy consumed in the factory 5 fans of 70 W each for 12 hours
E2 = 5 x 70 x 12 = 4200 W h = 4.2 kW h
∴ Total electricity consumed E = E1 + E2 = 6.0 + 4.2 = 10.2 kW h = 10.2 units
∴ Total expenditure @ Rs. 2.00 per unit = 2 x 10.2 = Rs. 20.4
Q.21. (a) A moving body of mass 20 kg has 40 joules of kinetic energy. Calculate its speed.
(b) A person carrying a load of 20 kg climbs 4 m in 10 seconds. Calculate the work done and his power, (g = 10 m/s2) [2016]
Ans: Given: Mass, m = 20 kg; Kinetic energy, Ek = 40 J;
= 2 m/s
(b) Given: Mass, m = 20 kg; Height, h = 4 m; Time, t = 10 s; g = 10 ms-2
Work done, W = mgh
= 20 x 10 x 4 = 800 J
and
Long Answer Type Questions
Q.1. (a) Define work. Give SI unit of work. Write an expression for positive work done.
(b) Calculate the work done in pushing acai through a distance of 50 m against the force of friction equal to 250 N. Also state the type of work done.
(c) Sarita lives on 3rd floor of building at the height of 15 m. She carries her school ba weighting 5.2 kg from the ground floor to her house. Find the amount of work done by her and identity the force against which she has done work (g = 10 ms-2) [2016]
Ans: (a) Work is said to be done if an applied force displaces a body in its own direction.
Its SI unit is joule (J).
Positive work done, W = F.s,
where F = force; 5 = displacement is direction of force.
(b) Given: Distance, s = 50 m; Force, f = 250
N (opposite to direction of friction)
Work, W = F .s = 250N x 50m = 12500 J Work done by applied force is positive and by friction is negative.
(c) Given: Mass, m = 5.2 kg; g = 10 m s-2; height h = 15 m
Work done = mgh = 5.2 x 10 x 15 = 780 J
Work is done against the force of gravity acting on the bag.
Q.2. (a) Define kinetic energy. Obtain an expression for the kinetic energy of an object.
(b) A ball of mass 400 g rolls on a ground with a uniform speed of 25 ms-1. Find the kinetic energy possessed by it. [2016]
Ans: (a) Kinetic energy of an object is the energy possessed by it by virtue of its state of motion. Every moving object possesses kinetic energy.
Consider an object of mass m in a state of motion with an initial velocity u. Let now a constant force F acts on it and displaces the body through a distance s in the direction of force applied.
∴ Work was done on the object W = Fs
Due to the work done on the body, let velocity of the object changes from u to v and a be the acceleration produced.
Then according to the equation of motion
v2 - u2 = 2as
⇒
Again according to second law of motion,
we have F = ma
∴ Work was done on the object W = Fs = (ma)
If the object started from rest, then u = 0 and hence W =
The work done on the object is equal to the kinetic energy imparted to the object. Thus, the kinetic energy possessed by an object of mass m moving with a uniform velocity v is given by
(b) Here mass of ball m = 400 g - 0.4 kg and speed of ball v = 25 m s-1.
∴ Kinetic energy of ball Ek =
Q.3. Calculate the electricity bill amount for a month of 30 days, if the following devices are used as specified :
(a) 3 bulbs of 40 W for 6 hours.
(b) 4 tube light of 50 W for 6 hours.
(c) A refrigerator of 320 W for 24 hours.
Given the rate of electricity is Rs. 2.50 per unit. [2015]
Ans: As per data given energy consumed per day in kW h units is :
(a) for using 3 bulbs of 40 W each of 6 hours
(b) for using 4 tube lights of 50 W each for 6 hours
(c) for running a refrigerator of 320 W for 24 hours
∴ Total energy consumed per day E - E1 + E2 + E3 = 0.72 + 1.2 + 7.68 = 9.60 kW h
∴ Total energy consumed during a month of 30 days = 30 x 9.60 kW h = 288 units
∴ Electricity bill @ Rs. 2.50 per unit - Rs. 2.50 x 288 = Rs. 720
Q.4. (a) Define the work done by a constant force. Write its SI unit and define this unit.
(b) A 3000 kg truck moving at a speed of 72 km/h stops after covering some distance. The force applied by brakes is 24000 N. Compute the distance covered and work done by this force. [2015]
Ans: (a) Work done on an object is defined as the magnitude of the force acting on the object multiplied by the distance moved by the object in the direction of the applied force.
∴ Work (W) = Constant force applied (F) x Displacement along the direction of force (s).
⇒ SI unit of work is called joule (JorMjm). Work is said to be 1 joule if under the influence of a force of 1 N the object moves} through a distance of 1 m along the direction of applied force.
(b) Here mass of truck m = 3000 kg, initial speed u = 72 km/h
final speed u = 0 and force applied by brakes F - 24000 N
As force of brakes opposes motion we take it negatively, that is F = 24000 N
∴ Acceleration of truck a =
Using the relation v2 - u2 = 2as, we have
Distance covered
and work done by the force W = Fs = (- 24000) x 25 = - 600000 J = -6x 105 J
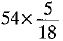m/s = 15 m/s; v = 0;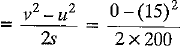
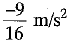
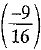
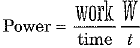
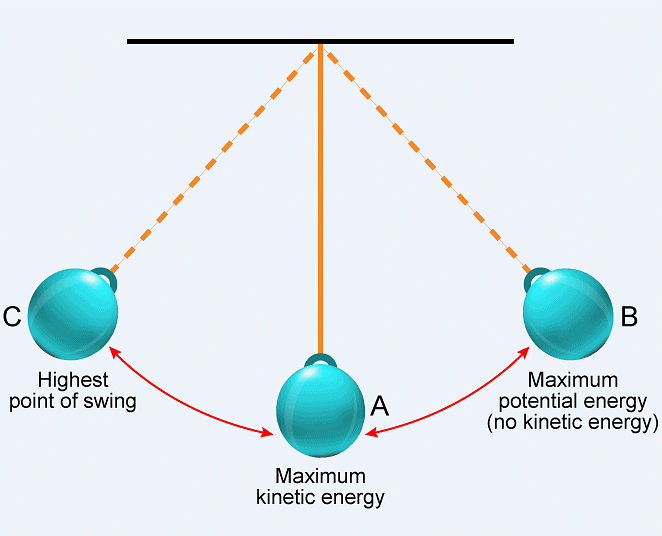Illustration of Law of Conservation of Energy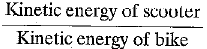
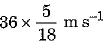
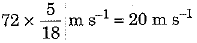
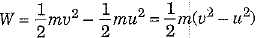
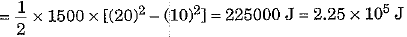
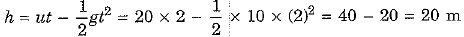
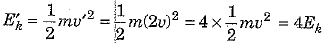
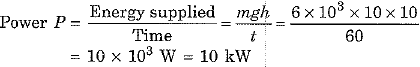
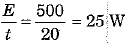
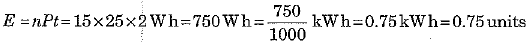
= Gravitational potential energy before falling = msh = 10 x 10 x 1 = 100J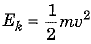
, hence velocity v = 
