Classification of Second Order PDEs - Partial Differential Equations, CSIR-NET Mathematical Sciences | Mathematics for IIT JAM, GATE, CSIR NET, UGC NET PDF Download
Second order partial differential equations in two variables
The general second order partial differential equations in two variables is of the form
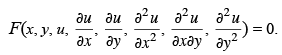 |
The equation is quasi-linear if it is linear in the highest order derivatives (second order), that is if it is of the form
| a(x, y, u, u x, u y)u xx + 2 b(x, y, u, ux, u y)u xy + c(x, y, u, u x, u y)u yy = d(x, y, u, u x, u y) |
We say that the equation is semi-linear if the coefficients a, b, c are independent of u. That is if it takes the form
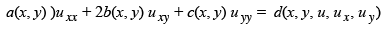 |
Finally, if the equation is semi-linear and d is a linear function of u, u x and u y, we say that the equation is linear. That is, when F is linear in u and all its derivatives.
We will consider the semi-linear equation above and attempt a change of variable to obtain a more convenient form for the equation.
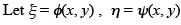 be an invertible transformation of coordinates. That is,
be an invertible transformation of coordinates. That is,

By the chain rule
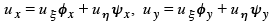
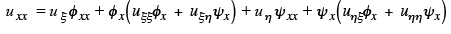
 first order derivatives of u
first order derivatives of u
Similarly,
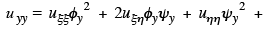 first order derivatives of u
first order derivatives of u
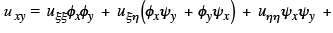 first order derivatives of u
first order derivatives of u
Substituting into the partial differential equation we obtain,
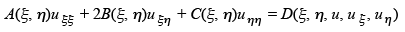 |
where
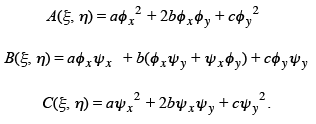
It easily follows that
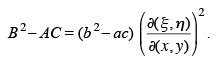
Therefore B2 - AC has the same sign as b2 - ac. We will now choose the new coordinates 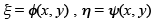 to simplify the partial differential equation.
to simplify the partial differential equation.
 constant defines two families of curves in R2. On a member of the family φ (x, y) = constant, we have that
constant defines two families of curves in R2. On a member of the family φ (x, y) = constant, we have that
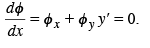
Therefore substituting in the expression for 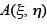 we obtain
we obtain
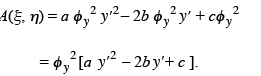
We choose the two families of curves given by the two families of solutions of the ordinary differential equation
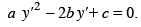
This nonlinear ordinary differential equation is called the characteristic equation of the partial differential equation and provided that a ≠ 0, b2 - ac > 0 it can be written as
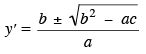 |
For this choice of coordinates 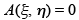 and similarly it can be shown that
and similarly it can be shown that 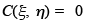 also. The partial differential equation becomes
also. The partial differential equation becomes
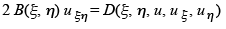
where it is easy to show that 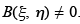 Finally, we can write the partial differential equation in the normal form
Finally, we can write the partial differential equation in the normal form
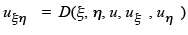 |
The two families of curves φ(x, y) = constant ,ψ(x, y) = constant obtained as solutions of the characteristic equation are called characteristics and the semi-linear partial differential equation is called hyperbolic if b2 - ac > 0 whence it has two families of characteristics and a normal form as given above.
If b2 - ac <0, then the characteristic equation has complex solutions and there are no real characteristics. The functions φ(x, y), φ(x, y) are now complex conjugates . A change of variable to the real coordinates

results in the partial differential equation where the mixed derivative term vanishes,
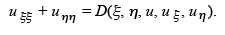 |
In this case the semi-linear partial differential equati on is called elliptic if b2 - ac < 0. Notice that the left hand side of the normal form is the Laplacian. Thus Laplaces equation is a special case of an elliptic equation (with D = 0).
If b2– ac = 0 , the characteristic equation 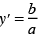 has only one family of solutions ψ(x, y) = constant. We make the change of variable
has only one family of solutions ψ(x, y) = constant. We make the change of variable
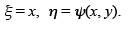
Then


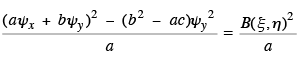
Also since ψ (x, y) = constant,
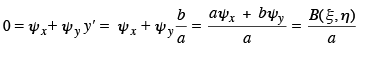
Therefore 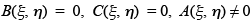 and the normal form in the case b2 – ac = 0 is
and the normal form in the case b2 – ac = 0 is
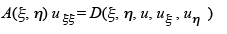
or finally
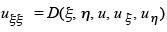 |
The partial differential equation is called parabolic in the case b2 - a = 0. An example of a parabolic partial differential equation is the equation of heat conduction
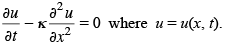
Example 1. Classify the following linear second order partial differential equation and find its general solution .
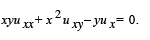
In this example 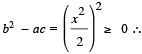 the partial differential equation is hyperbolic provided x ≠ 0, and parabolic for x = 0.
the partial differential equation is hyperbolic provided x ≠ 0, and parabolic for x = 0.
For x ≠ 0 the characteristic equations are
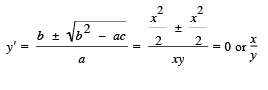
If y' = 0, y = constant.
If 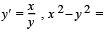 constant. Therefore two families of characteristics are
constant. Therefore two families of characteristics are
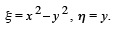
Using the chain rule a number of times we calculate the partial derivatives
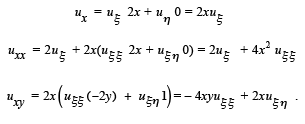
Substituting into the partial differential equation we obtain the normal form
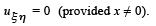
Integrating this equation with respect to η
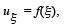
where f is an arbitrary function of one real variable. Integrating again with respect to 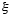
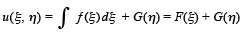
where F, G are arbitrary functions of one real variable. Reverting to the original coordinates we find the general solution
Example 2. Classify, reduce to normal form and obtain the general solution of the partial differential equation
For this equation  the equation is parabolic everywhere in the plane (x , y ). The characteristic equation is
the equation is parabolic everywhere in the plane (x , y ). The characteristic equation is
Therefore there is one family of characteristics y/s = constant.
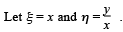 Then using the chain rule,
Then using the chain rule,
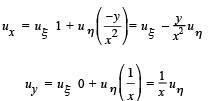
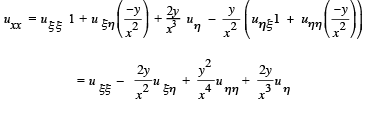
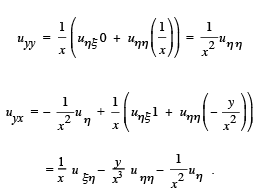
Substituting into the partial differential equation we obtain the normal form
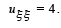
Integrating with respect to 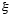
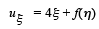
where f is an arbitrary function of a real variable. Integrating again with respect to 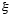
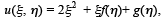
Therefore the general solution is given by
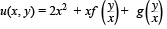
where f, g are arbitrary functions of a real variable.
|
556 videos|198 docs
|
FAQs on Classification of Second Order PDEs - Partial Differential Equations, CSIR-NET Mathematical Sciences - Mathematics for IIT JAM, GATE, CSIR NET, UGC NET
| 1. What are the different types of second-order partial differential equations? |  |
| 2. How can second-order partial differential equations be classified based on their coefficients? |  |
| 3. What is the general form of a second-order partial differential equation? |  |
| 4. How are boundary conditions used in solving second-order partial differential equations? |  |
| 5. What are some applications of second-order partial differential equations? |  |
|
556 videos|198 docs
|

|
Explore Courses for Mathematics exam
|

|

















