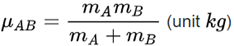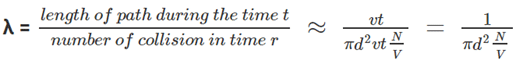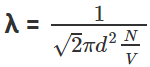Collision Theory, Mean Free Path & viscosity of gases | Physical Chemistry PDF Download
| Table of contents |

|
| Collision Theory |

|
| Collision Frequency |

|
| Concept of Mean Free Path |

|
| Derivation of Mean Free Path |

|
Collision Theory
Collision theory states that for a chemical reaction to occur, the reacting particles must collide with one another.
The rate of the reaction depends on the frequency of collisions. The three main points of collision theory for a chemical reaction to take place are:
- Reacting substances must collide
- The colliding particles should have sufficient energy
- The substances must collide in a set orientation.
Collision diameter is defined as the distance between the centers of two colliding molecules when at their closest point of approach. Collision diameter is inversely proportional to the molecular mass of the molecule. This is because the molecules with higher molecular mass have a greater radius.
d α 1/M
Since the size of the atom is big, there is a lot of free space and the electron density is relatively less. Due to this the atoms can come close due to reduced electron-electron repulsions. Let us calculate the molecular mass of the molecules mentioned in the options:
H2 has a molecular mass of 2 g
He has a molecular mass of 4 g
CO2 has a molecular mass of 44 g
N2 has a molecular mass of 28 g
CO2 has the highest molecular mass and will have the least collision diameter.
Collision Frequency
Collision frequency describes the rate of collisions between two atomic or molecular species in a given volume, per unit time.
In an ideal gas, assuming that the species behave like hard spheres, the collision frequency between A and B is: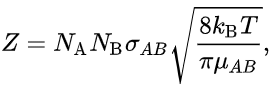
SI unit of Z is number of collision per time m3s-1.
where:
- NA is the number of A molecules in the gas,
- NB is the number of B molecules in the gas,
- σAB is the collision cross-section (unit m2), the area when two molecules collide with each other, simplified to σAB = π(rA + rB)2, where rA the radius of A and rB the radius of B.
- kB is the Boltzmann's constant (unit m2 kg s-2 K-1)
- T is the temperature (unit K),
- μAB is the reduced mass of the reactants A and B,

Concept of Mean Free Path
The mean free path λ of a gas molecule is its average path length between collisions
Mathematically the mean free path can be represented as follows: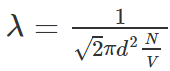
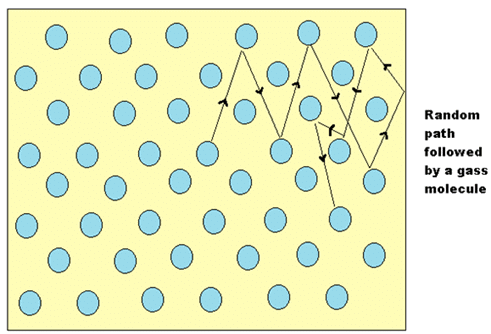
- Let’s look at the motion of a gas molecule inside an ideal gas, a typical molecule inside an ideal gas will abruptly change its direction and speed as it collides elastically with other molecules of the same gas.
- Though between the collisions the molecule will move in a straight line at some constant speed, this is applicable for all the molecules in the gas.
- It is difficult to measure or describe this random motion of gas molecules thus we attempt to measure its mean free path λ.

- As its name says λ is the average distance travelled by any molecule between collisions, we expect λ to vary inversely with N/V, which is the number of molecules per unit volume or the density of molecules because if there are more molecules more are the chances of them colliding with each other hence reducing the mean free path, and also λ would be inversely proportional to the diameter d of the molecules, because if the molecules were point masses then they would never collide with each other, thus larger the molecule smaller the mean free path, and it should be proportional to π Times Square of the diameter and not the diameter itself because we consider the circular cross-section and not the diameter itself.
Derivation of Mean Free Path
- We will derive the equation using the following assumptions, let’s assume that the molecule is spherical, and the collision occurs when one molecule hits the other, and only the molecule we are going to study will be in motion and rest molecules will be stationary.
- Let’s consider our single-molecule to have a diameter of d and all the other molecules to be points this does not change our criteria for collision, as our single-molecule moves through the gas, it sweeps out a short cylinder of cross-section area πd2 between successive collisions, for a small-time t it will move a distance of vt where v is the velocity of the molecule, now if we sweep this cylinder we will get a volume of πd2*vt so the number of point molecules inside this volume will give us the number of collisions the molecule might have,
- Since N/V is the number of molecules per unit volume, the number of molecule in the cylinder will be N/V multiplied by the volume of cylinder i.e.πd2vt, the mean free path can be derived as follows,

- Why we have approximated the equation is because we have assumed that all the particles are stationary with respect to the particle we are studying, in fact, all the molecules are moving relative to each other, we have cancelled two velocities in the above equation but actually the v in the numerator is the average velocity and v In the denominator is relative velocity hence they both differ from each other with a factor √2, therefore, the final equation would be,

Mean free path at sea level is 0.1 micrometer.
|
83 videos|142 docs|67 tests
|
FAQs on Collision Theory, Mean Free Path & viscosity of gases - Physical Chemistry
| 1. What is collision theory? |  |
| 2. How is collision frequency defined? |  |
| 3. What is the concept of mean free path? |  |
| 4. How is the mean free path derived? |  |
| 5. How does collision theory relate to the viscosity of gases? |  |

|
Explore Courses for Chemistry exam
|

|