Completing the square | Mathematics for Grade 12 PDF Download
Introduction
- Completing the square is a method in algebra that is used to write a quadratic expression in a way such that it contains the perfect square. In simple words, we can say that completing the square is a process where consider a quadratic equation of the ax2 + bx + c = 0 and change it to write it in the form a(x + p)2 + q = 0. This method is generally used to find the roots of a quadratic equation.
Completing the Square Method
- The most common application of completing the square method is factorizing a quadratic equation, and henceforth finding the roots or zeros of a quadratic polynomial or a quadratic equation. We know that a quadratic equation of the form ax2 + bx + c = 0 can be solved by the factorization method. But sometimes, factorizing the quadratic expression ax2 + bx + c is complex or NOT possible. Let us have a look at the following example to understand this case.
For example:
- x2 + 2x + 3 cannot be factorized as we cannot find two numbers whose sum is 2 and whose product is 3. In such cases, we write it in the form a(x + m)2 + n by completing the square. Since we have (x + m) whole squared, we say that we have "completed the square" here.
Completing the Square Formula
- Completing the square formula is a technique or method to convert a quadratic polynomial or equation into a perfect square with some additional constant. A quadratic expression in variable x: ax2 + bx + c, where a, b and c are any real numbers but a ≠ 0, can be converted into a perfect square with some additional constant by using completing the square formula or technique.
Note: Completing the square formula is used to derive the quadratic formula.
Completing the square formula is a technique or method that can also be used to find the roots of the given quadratic equations, ax2 + bx + c = 0, where a, b and c are any real numbers but a ≠ 0.
Formula for Completing the Square:
- The formula for completing the square is: ax2 + bx + c ⇒ a(x + m)2 + n
- where, m is any real number and n is a constant term.
- Instead of using the complex step-wise method for completing the square, we can use the following simple formula to complete the square. To complete the square in the expression ax2 + bx + c, first find:
- m = b/2a and n = c - (b2/4a)
- Substitute these values in: ax2 + bx + c = a(x + m)2 + n. These formulas are derived geometrically. Let us study this in detail using illustrations in the following sections.
Completing the Square Formula Examples
Example 1: Using completing the square formula, find the number that should be added to x2 - 7x in order to make it a perfect square trinomial.
The given expression is x2 - 7x.
Method 1:
- Comparing the given expression with ax2 + bx + c, a = 1; b = -7
Using the formula, the term that should be added to make the given expression a perfect square trinomial is,
(b/2a)2 = (-7/2(1))2 = 49/4.
Thus, from both the methods, the term that should be added to make the given expression a perfect square trinomial is 49/4.Method 2:
- The coefficient of x is -7. Half of this number is -7/2. Finding the square, (-7/2)2 = 49/4
Example 2: Use completing the square formula to solve: x2 - 4x - 8 = 0.
Method 1:
- Using formula, ax2 + bx + c = a(x + m)2 + n. Here, a = 1, b = -4, c = -8
⇒ m = b/2a = (-4)/2(1) = -2
and, n = c - (b2/4a) = -8 - (-4)2/4(1) = -12
⇒ x2 - 4x - 8 = (x - 2)2 - 12.
⇒ (x - 2)2 = 12
⇒ (x - 2) = ±√12
⇒ x - 2 = ± 2√3
⇒ x = 2 ± 2√3Method 2:
- Let’s transpose the constant term to the other side of the equation: x2 - 4x = 8. Take half of the coefficient of the x-term, which is -4, including the sign, which gives -2. Square -2 to get +4, and add this squared value to both sides of the equation:
x2 - 4x + 4 = 8 + 4
⇒ x2 - 4x + 4 = 12- This process creates a quadratic expression that is a perfect square on the left-hand side of the equation. Simply we can replace the quadratic with the squared-binomial form: (x - 2)2 = 12
- Now, we've completed the expression to create a perfect-square binomial, let’s solve:
(x - 2)2 = 12
⇒ (x - 2) = ±√12
⇒ x - 2 = ± 2√3
⇒ x = 2 ± 2√3
Using completing the square method, x = 2 ± 2√3.
Solving Quadratic Equations Using Completing the Square Method
- Let us complete the square in the expression ax2 + bx + c using the square and rectangle in Geometry. Based on the method studied earlier, the coefficient of x2 must be made '1' by taking 'a' as the common factor. We get, ax2 + bx + c = a[x2 + (b/a)x + (c/a)]. Now, we will consider the first two terms, x2 and (b/a)x. Let us consider a square of side 'x' (whose area is x2). Let us also consider a rectangle of length (b/a) and breadth (x) (whose area is (b/a)x).
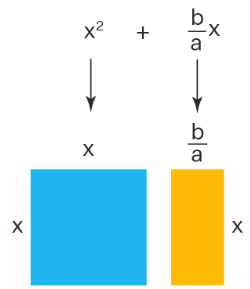
- Now, divide the rectangle into two equal parts. The length of each rectangle will be b/2a.
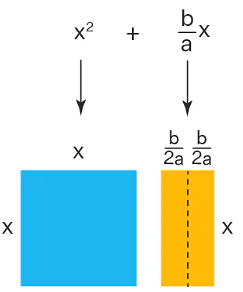
- Attach half of this rectangle to the right side of the square and the remaining half to the bottom of the square.
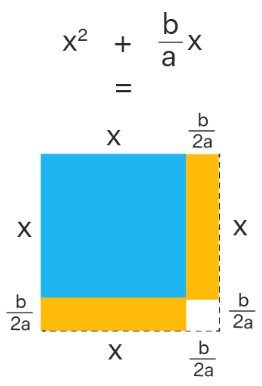
To complete a geometric square, there is some shortage which is a square of side b/2a. The square of area [(b/2a)2] should be added to x2 + (b/a)x to complete the square. But, we cannot just add, we need to subtract it as well to retain the expression's value. Thus, to complete the square:
x2 + (b/a) x = x2 + (b/a)x + (b/2a)2 - (b/2a)2
= x2 + (b/a)x + (b/2a)2 - b2/4a2
Multiplying and dividing (b/a)x with 2 gives, x2 + (2⋅x⋅b/2a) + (b/2a)2 - b2/4a2
By using the identity, x2 + 2xy + y2 = (x + y)2
The above equation can be written as,
x2 + (b/a) x = (x + b/2a)2 - (b2/4a2)
By substituting this in (1): ax2 + bx + c = a((x + b/2a)2 - b2/4a2 + c/a) = a(x + b/2a)2 - b2/4a + c = a(x + b/2a)2 + (c - b2/4a)
This is of the form a(x + m)2 + n, where,
m = b/2a
n = c - (b2/4a)
Example: We will complete the square in -4x2 - 8x - 12 using this formula. Comparing this with ax2 + bx + c, a = -4; b = -8; c = -12
Find the values of 'm' and 'n' using:
m = b/2a = -8/2(-4) = 1
n = c - (b2/4a) = -12 - (-8)2/4(-4) = -8
Substitute these values in: ax2 + bx + c = a(x + m)2 + n
We get: - 4x2 - 8x - 12 = -4(x + 1)2 - 8
Completing the Square Steps
To apply the method of completing the square, we will follow a certain set of steps. Given below is the process of completing the square stepwise:
- Step 1: Write the quadratic equation as x2 + bx + c. (Coefficient of x2 needs to be 1.)
- Step 2: Determine half of the coefficient of x.
- Step 3: Take the square of the number obtained in step 1.
- Step 4: Add and subtract the square obtained in step 2 to the x2 term.
- Step 5: Factorize the polynomial and apply the algebraic identity x2 + 2xy + y2 = (x + y)2 to complete the square.
How to Apply Completing the Square Method?
Example: Complete the square in the expression -4x2 - 8x - 12.
First, we should make sure that the coefficient of x2 is '1'. If the coefficient of x2 is NOT 1, we will place the number outside as a common factor. We will get:
-4x2 - 8x - 12 = -4(x2 + 2x + 3)Now, the coefficient of x2 is 1.
- Step 1: Find half of the coefficient of x. Here, the coefficient of 'x' is 2. Half of 2 is 1.
- Step 2: Find the square of the above number. 12 = 1
- Step 3: Add and subtract the above number after the x term in the expression whose coefficient of x2 is 1. This means, -4(x2 + 2x + 3) = -4(x2 + 2x + 1 - 1 + 3)
- Step 4: Factorize the perfect square trinomial formed by the first 3 terms using the identity x2 + 2xy + y2 = (x + y)2. In this case, x2 + 2x + 1 = (x + 1)2. The above expression from Step 3 becomes: -4(x2 + 2x + 1 - 1 + 3) = -4((x + 1)2 - 1 + 3)
- Step 5: Simplify the last two numbers. Here, -1 + 3 = 2. Thus, the above expression is: -4x2 - 8x - 12 = -4(x + 1)2 - 8. This is of the form a(x + m)2 + n. Hence, we have completed the square. Thus, -4x2 - 8x - 12 = -4(x + 1)2 - 8
Note: To complete the square in an expression ax2 + bx + c
- Make sure the coefficient of x2 is 1.
- Add and subtract (b/2)2 after the 'x' term and simplify.
Trick to Learn Completing the Square Method
Here are a few tips for completing the square technique.
- Step 1: Note down the form we wish to obtain after completing the square: a(x + m)2 + n
- Step 2: After expanding, we get, ax2 + 2amx + am2 + n
- Step 3: Compare the given expression, say ax2 + bx + c and find m and n as m = b/2a and n = c - (b2/4a).
|
174 videos|101 docs|119 tests
|




















