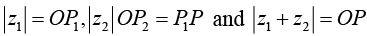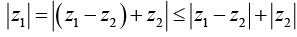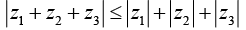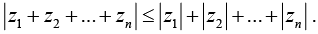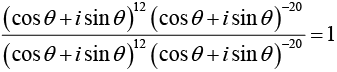Complex Numbers | Mathematical Methods - Physics PDF Download
| Table of contents |

|
| Basic Properties |

|
| Functions in the Complex Domain |

|
| Polar Representation |

|
| Complex Numbers of Unit Magnitude |

|
| Circular and Hyperbolic Functions |

|
| Inverse Hyperbolic Functions |

|
| Logarithm |

|
Complex numbers and analysis based on complex variable theory have become extremely important and valuable tools for the mathematical analysis of physical theory. Though the results of the measurement of physical quantities must be described by real numbers, there is ample evidence that successful theories predicting the results of those measurements require the use of complex numbers and analysis.
Basic Properties
A complex number is nothing more than an ordered pair of two real numbers, {a,b). Similarly, a complex variable is an ordered pair of two real variables,
z ≡ {x,y).
The ordering is significant. In general to (a,b) is not equal to (b,a) and (x,v) is not equal to(y,x). As usual, we continue writing a real number (x,0) simply as x, and we call / = (0, 1) the imaginary unit. All of complex analysis can be developed in terms of ordered pairs of numbers, variables, and functions (h(x, y),v(x, y)).
We now define addition of complex numbers in terms of their Cartesian components as
z1 + z2 = (x1,y2) + (x2,y2) = (X1 + x2,y1, + y2) .
Multiplication of complex numbers is defined as
z1z2 = (x1, V1).(x2, y2) = (x1X2 - V1y2, x1y2 + x2y1)
It is obvious that multiplication is not just the multiplication of corresponding components. Thus i2 = (0,1).(0,1) = (-1,0) = -1, so we can also identify i = √-1 as usual, and further rewrite z = (x,y) = (x, 0) + (0, y) = x + (0,1). (y, 0) = x + iy .
Clearly, introduction of the symbol /' is not necessary here, but it is convenient, in large part because the addition and multiplication rules for complex numbers are consistent with those for ordinary arithmetic with the additional property that i2 = -1:
(X1 + iy1)(x2 + iy2) = X1X2 + i2y1y2 + i (x1y2 + y1x2) = (X1X2 - y1y2) + i (x1y2 + y1x2).
For historical reasons,i and its multiples are known as imaginary numbers,
- The space complex numbers sometimes denoted Z by mathematicians, has the following formal properties:
- It is closed under addition and multiplication, meaning that if two complex numbers are added or multiplied, the result is also a complex number.
- It has a unique zero number, which when added to any complex number leaves it unchanged and which, when multiplied with any complex number yields zero.
- It has a unique unit number, 1, which when multiplied with any complex number leaves it unchanged.
- Every complex number z has an inverse under addition (known as -z), and every nonzero has an inverse under multiplication, denoted z_1 or 1 / z
- It is closed under exponentiation: if u and v care complex numbers u' is also a complex number.
Some additional definitions and properties include the following:
Complex conjugation: Like all complex numbers, i has an inverse under addition, denoted -i, in two-component form, (0,-1). Given a complex number z = x + iy, it is useful to define another complex number, z* = x - iy , which we call the complex conjugate of z . Forming
zz* = (x + iy) (x - iy) = x2 + y2
we see that zz* is real; we define the absolute value of z, denoted |z|, as 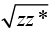
The complex conjugate of z is often denoted 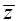 a in the mathematical literature.
a in the mathematical literature.
Division: Consider now the division of two complex numbers: z'/z . We need to manipulate this quantity to bring it to the complex number form u + iv (with u and v real). We may do so as follows: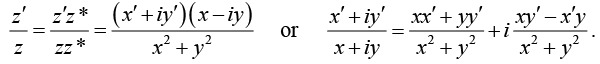
Functions in the Complex Domain
Since the fundamental operations in the complex domain obey the same rules as those for arithmetic in the space of real numbers, it is natural to define functions so that their real and complex incarnations are similar, and specifically so that the complex and real definitions agree when both are applicable. This means, other things, that if a function is represented by a power series, we should, within the region of convergence of the power series be able to use such series with complex values of the expansion variable. This is called permanence of the algebraic form.
Applying this concept to the exponential, we define
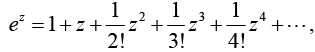
Now, replacing z by i z. wc have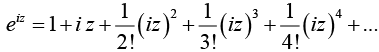
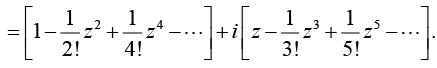
It was permissible to regroup the terms because that series is absolutely convergent for all z . If we now identify the bracketed expansions in the last line as cos z and sin z, we have the extremely valuable result
eiz = cos z + i sin z .
This result is valid for all z, real, imaginary, or complex, but is particularly useful when z is real.
Any function w (z) of a complex variable z = x + iy can in principle be divided into real
and imaginary parts, just as we did when we added, multiplied, or divided complex numbers. That is, we can write
w(z) = u(x,y) + iv(x,y),
in which the separate functions u(x, y) and v(x, y)are pure real.
For example, if f (z) = z2, we have
f (z) = (z + iy)2 = (x2 - y2) + i (2xy)
The real part of a function f(z) will be labeled 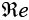 f (z) whereas the imaginary part will be labeled Im f (z).
f (z) whereas the imaginary part will be labeled Im f (z).
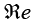 w(z) = u(x,y) , Imw(z) = v(x,y) .
w(z) = u(x,y) , Imw(z) = v(x,y) .
The complex conjugate of our function w(z) is u(x,y) -iv(x,y), and depending on w may or may not be equal to w (z *) .
Polar Representation
We may visualize complex numbers by assigning them locations on a planar graph, called an Argand diagram or the complex plane. Traditionally the real component is plotted horizontally, on what is called the real axis, with the imaginary axis in the vertical direction.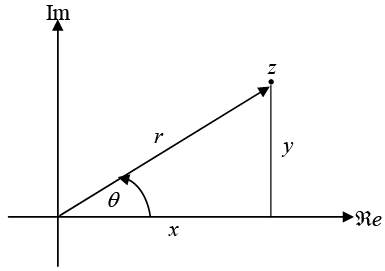
Argand diagram, showing location of z = x + iy = reiθ
An alternative to identifying points by their Cartesian coordinates (x,y) is to use polar coordinates (r, θ), with
x = r cos θ, y = r sin θ, or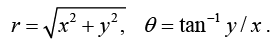
The arctan function tan -1 (y / x) multiple valued; the correct location on an Argand diagram needs to be consistent with the individual values of x and y .
The Cartesian and polar representations of a complex number can also be related by writing
x + iy = r (cos θ + i sin) = reiθ .
Note that r is also|z|, so the magnitude of z is given by its distance from the origin in an
Argand diagram. In complex variable theory, r is also called the modulus of z and θ is termed the argument or the phase of z .
If we have two complex numbers, z and z' in polar form, their product zz' can be written 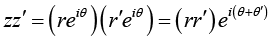
showing that the location of the product in an Argand diagram will have argument (polar angle) at the sum of the polar angles of the factors and with a magnitude that is the product of their magnitudes. Conversely, the quotient z/z' will have magnitude r I r' and argument d - d'. These relationships should aid in getting a qualitative understanding of complex multiplication and division. This discussion also shows that multiplication and division are easier in the polar representation, whereas addition and subtraction have simpler forms in Cartesian coordinates.
The plotting of complex numbers on an Argand diagram makes obvious some other properties. Since addition on an Argand diagram is analogous to 2 -D vector addition, it can be seen that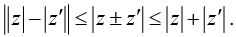
Also, since z* = re-iθ has the same magnitude z as a but an argument that differs only in sign, z + z * will be real and equal to 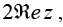 , while z-z* will be pure imaginary and equal to 2iImz.
, while z-z* will be pure imaginary and equal to 2iImz.
An illustration of this discussion is shown in figure below.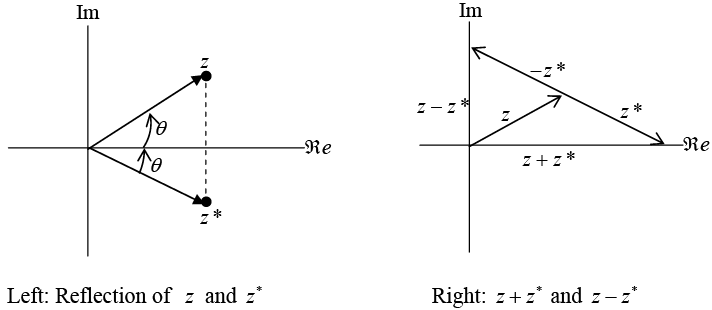
We can use an Argand diagram to plot values of a function w (z) as well as just z itself, in which case we could label the axes u and v, referring to the real and imaginary parts of w . In that case, we can think of the function w(z) as providing a mapping from the plane to the uv plane, with the effect that any curve in the xy (sometimes called z) plane is mapped into a corresponding curve in the nv(= w) plane. In addition, the statements of the preceding paragraph can be extended to functions: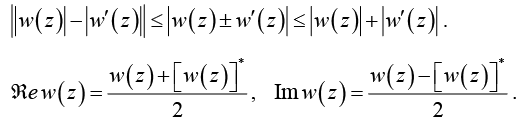
Example 1: If z1, z2 be any two complex numbers prove that
(i) 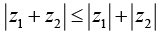 i.e., [the modulus of the sum of two complex numbers is less than or at the most equal to the sum of their moduli]
i.e., [the modulus of the sum of two complex numbers is less than or at the most equal to the sum of their moduli]
(ii) 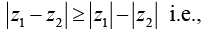 [the modulus of the difference of two complex number is greater than or at the most equal to the difference of their moduli].
[the modulus of the difference of two complex number is greater than or at the most equal to the difference of their moduli].
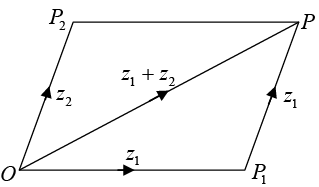
(i) Let P1,P2 represent the complex numbers z1, z2.
Complete the parallelogram OP1PP2, so that
Now from AOP1P, OP < OP1 + P1P , the sign of equality corresponding to the case when 0,P1,P are collinear.
Hence(i)
Again
Thus(ii)
Corollary,
In general,
Complex Numbers of Unit Magnitude
Complex numbers of the form
eiθ = cosθ + i sinθ,
where we have given the variable the name θ to emphasize the fact that we plan to restrict it to real values, correspond on an Argand diagram to points for which x = cosθ,y = sinθ, and whose magnitude is therefore cos2θ + sin2θ = 1.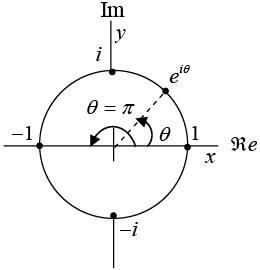
Some values of z on the unit circle.
The point's exp(iθ) therefore lie on the unit circle, at polar angleθ. This observation makes obvious a number of relations that could in principle also be deduced fromeiθ =cosθ + i sinθ . For example, if θ has the special values π/2,π or 3π/2, we have the interesting relationships
eiπ/2 = i,eiπ =-1, e3iπ/2 = -i
We also see that exp (iθ) is periodic, with period 2π, so
A few relevant values of z on the unit circle are illustrated in figure above. These relationships cause the real part of exp(iωt) to describe oscillation at angular
frequency ω, with exp(i[ωt+ δ) describing an oscillation displaced from that first mentioned by a phase difference δ.
Circular and Hyperbolic Functions
The relationship eiθ = cosθ + i sin θ enables us to obtain convenient formulas for the sine and cosine. Taking the sum and difference of exp (+iθ) and exp (-iθ), we have
These formulas place the definitions of the hyperbolic functions in perspective:
Comparing these two sets of equations, it is possible to establish the formulas
cosh iz = cos z, sinh iz = i sin z .
The fact that exp (inθ) can be written in the two equivalent fonts
cos nθ + i sin nθ = (cosθ + i sin θ)
establishes a relationship known as de Moivre's Theorem.
Example 2: Simplify 
We have (cos3θ + isin3θ)4 = cos 12θ +/sin 12θ = (cosθ + /sinθ)12
(cos 4θ - i sin 4θ)5 = (cos 20θ - i sin 20θ) = (cos θ + / sin θ)-20
(cos 4θ + i sin 4θ)3 = cos 12θ + i sin 12θ = (cos θ + / sin θ)12
(cos 5θ + i sin 5θ) -4 = cos 20θ - i sin 20θ = (cos θ + i sin θ)-20
The given expression =
Inverse Hyperbolic Functions
cos nθ + i sin nθ = (cos θ + i sin θ)n
By expanding the right hand side we easily obtain tringonometric multiple-angle formulas, of which the simplest examples are the well-known results
sin (2θ) = 2 sin θ cos θ, cos (2θ) = cos2θ - sin2θ.
(i)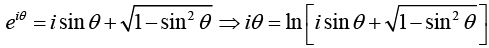
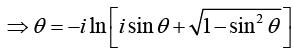
Setting sin θ = z and θ = sin-1 (z). we express the inverse trigonometric function in terms of logarithms 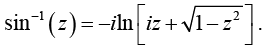
(ii) Similarly 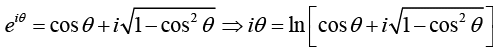
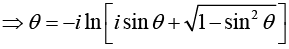
Setting cosθ = z and θ = cos-1 (z). we express the inverse trigonometric function in terms of logarithms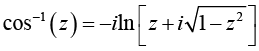
(iii) eiθ = cos θ + i sin θ ⇒ iθ = In [cos θ + i sin θ]
Setting tanθ = z and θ = tan-1 (z) . Thus cosθ = 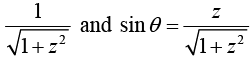
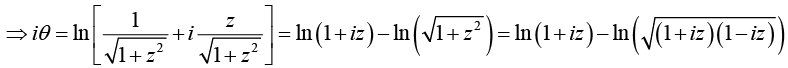

(iv) Show that sinh-1 (z) = In
Let sinh-1 z = u , then z = sinh u = 
This being a quadratic in eu, we have eu = 
∴ Taking the positive sign only, we have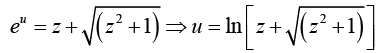
(v) Show that cosh-1 z = In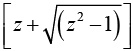
Let cosh-1 z = u , then z = cosh u = 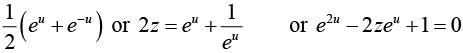
This being a quadratic in eu, we have eu = 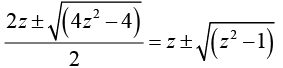
∴ the positive sign only, we have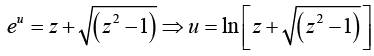
(v) Show that tanh-1 (z) =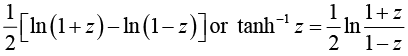
Let tanh-1 z = u . then z = tanh u = 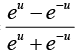
Applying componendo and dividendo, we get 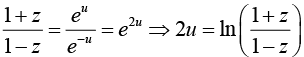
Powers and Roots
The polar form is very convenient for expressing powers and roots of complex numbers.
For integer powers, the result is obvious and unique:
For roots (fractional powers), we also have
but the result is not unique. If we write z in the alternate but equivalent form 
where m is an integer, we now get additional values for the root: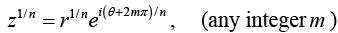
If n = 2 (corresponding to the square root), different choices of m will lead to two values of z1/2, both of the same modulus but differing in argument by π. This corresponds to the well-known result that the square root is double-valued and can be written with either sign.
In general, z1/n is n -valued, with successive values having arguments that differ by 2π/n . Figure below illustrates the multiple values of (l)1/3, (i)1/3 and(-l)1/3.
(1)1/3 = ei(θ + 2mπ)/3 where θ = θ and m = 0,1,2 .
(i)1/3 = ei(θ + 2mπ)/3 where θ = π/12 and m = 0,1,2 .
(i)1/3 = ei(θ+2mπ)/3 where θ = π and m = 0,1,2 .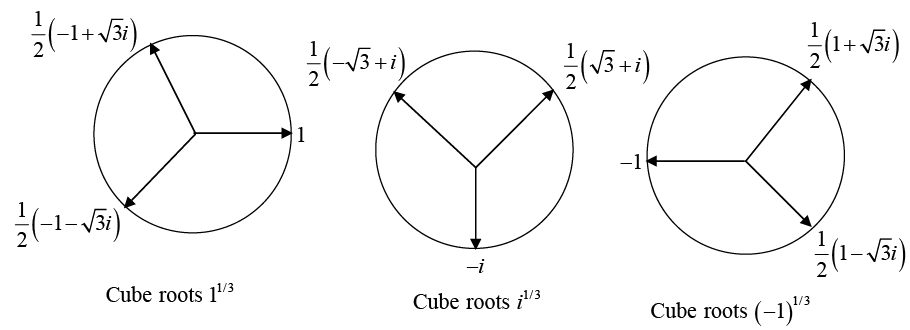
Logarithm
Another multivalued complex function is the logarithm, which in the polar representation takes the form
Inz = In (reiθ) = lnr + iθ
However, it is also true that
Inz = In(rei(θ+2nπ)) = lnr + i (θ + 2nπ),
for any positive or negative integer n . Thus, lnz has, for a given z , the infinite number of values corresponding to all possible choices ofn .
(i) Let z = x + iy = reiθ where r = 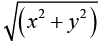 and θ =
and θ = 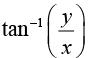
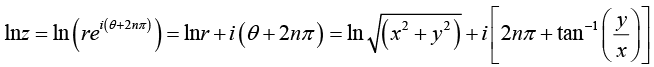
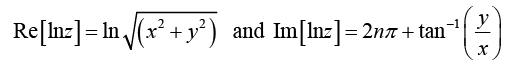
(ii) Real and imaginary parts of (α + iβ)x + iy
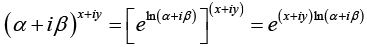
Put α = r cos θ, B = r sin θ so that r = 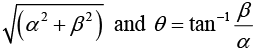
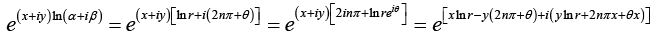
Compare with eA+iB = eA (cos B + /sin B)
where A = xIn r-y (2nπ + θ) and B = yIn r + x(2nπ + θ)
∴ The required real part = eA cos B and imaginary part = eA sin B
(iii) General value of ln(-i)
In (-i) = 2inπ + log [0 + i (-1)] put [0 = r cos θ, -1 = r sin θ ⇒ r = 1,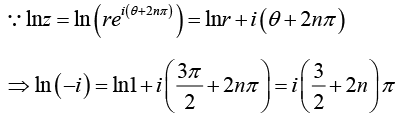
|
78 videos|18 docs|24 tests
|
FAQs on Complex Numbers - Mathematical Methods - Physics
| 1. What are the basic properties of complex numbers? |  |
| 2. What is the polar representation of a complex number? |  |
| 3. What are circular and hyperbolic functions in complex numbers? |  |
| 4. What are inverse hyperbolic functions in complex numbers? |  |
| 5. What is the logarithm of a complex number? |  |