Composition of Functions and Invertible Function | Algebra - Mathematics PDF Download
Suppose A is the father of B and B is the father of C. Who will be A for C? A is the grandfather of C. Here, we see that there is a relation between A and B, B and C and also between A and C. This relation between A and C denotes the indirect or the composite relation. In this section, we will get ourselves familiar with composite functions. Composite functions show the sets of relations between two functions. Let us start to learn the composition of functions and invertible function.
Composite Functions
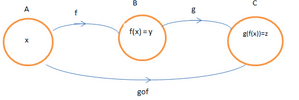
Suppose f is a function which maps A to B. And there is another function g which maps B to C. Can we map A to C? The mapping of elements of A to C is the basic concept of Composition of functions. When two functions combine in a way that the output of one function becomes the input of other, the function is a composite function.
In mathematics, the composition of a function is a step-wise application. For example, the function f: A→ B & g: B→ C can be composed to form a function which maps x in A to g(f(x)) in C. All sets are non-empty sets. A composite function is denoted by (g o f) (x) = g (f(x)). The notation g o f is read as “g of f”.
Consider the functions f: A→B and g: B→C. f = {1, 2, 3, 4, 5}→ {1, 4, 9, 16, 25} and g = {1, 4, 9, 16, 25} → {2, 8, 18, 32, 50}. A = {1, 2, 3, 4, 5}, B = {16, 4, 25, 1, 9}, C = {32, 18, 8, 50, 2}.Here, g o f = {(1, 2), (2, 8), (3, 18), (4, 32), (5, 50)}.
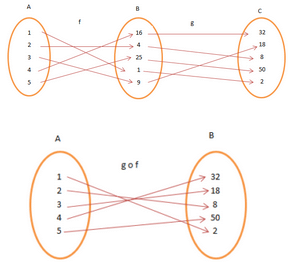
The composition of functions is associative in nature i.e., g o f = f o g. It is necessary that the functions are one-one and onto for a composition of functions.
Invertible Function
A function is invertible if on reversing the order of mapping we get the input as the new output. In other words, if a function, f whose domain is in set A and image in set B is invertible if f-1 has its domain in B and image in A.
f(x) = y ⇔ f-1 (y) = x.
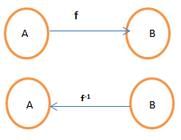
Not all functions have an inverse. For a function to have an inverse, each element b∈B must not have more than one a ∈ A. The function must be an Injective function. Also, every element of B must be mapped with that of A. The function must be a Surjective function. It is necessary that the function is one-one and onto to be invertible, and vice-versa.
It is interesting to know the composition of a function and its inverse returns the element of the domain.
f-1 o f = f -1 (f(x)) = x
Solved Examples for You
Problem: If f: A → B, f(x) = y = x2 and g: B→C, g(y) = z = y + 2 find g o f.
Given A = {1, 2, 3, 4, 5}, B = {1, 4, 9, 16, 25}, C = {2, 6, 11, 18, 27}.
Solution: g o f(x) = g(f(x))
g(f(1)) = g(1) = 2, g(f(2)) = g(4) = 6, g(f(3)) = g(9) = 11, g(f(4)) = g(16) = 18, g(f(5)) = g(25) = 27.
Problem: Write the inverse of the above g o f.
Solution: (g o f) -1 = f-1(g-1(z))
f-1(g-1(z)) = f-1(g-1(2)) = f-1(1) = 1, f-1(g-1(6)) = f-1(4) = 2, f-1(g-1(11)) = f-1(9) = 3, f-1(g-1(18)) = f-1(16) = 4 & f -1(g-1(27)) = f-1(25) = 5.
|
161 videos|58 docs
|
FAQs on Composition of Functions and Invertible Function - Algebra - Mathematics
| 1. What is a composition of functions? |  |
| 2. How do you find the composition of functions? |  |
| 3. What does it mean for a function to be invertible? |  |
| 4. How do you determine if a function is invertible? |  |
| 5. Can a composition of invertible functions give an invertible function? |  |




















