Composition of Functions | The Complete SAT Course - Class 10 PDF Download

What is the Composition of Functions?

The composition of functions f(x) and g(x) where g(x) is acting first is represented by f(g(x)) or (f ∘ g)(x). It combines two or more functions to result in another function. In the composition of functions, the output of one function that is inside the parenthesis becomes the input of the outside function. i.e.,

• In f(g(x)), g(x) is the input of f(x).
• In g(f(x)), f(x) is the input of g(x).

We can understand this using the following figure: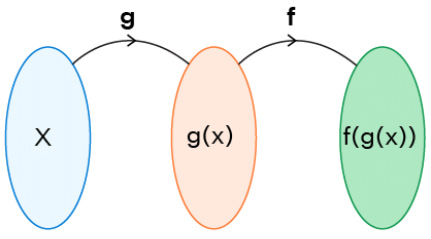

i.e., to find f(g(x)) (which is read as "f of g of x"), we have to find g(x) first and then we substitute the result in f(x).

Symbol of Composition of Functions

The symbol of the composition of functions is ∘. It can also be shown without using this symbol but by using the brackets. i.e.,

• (f ∘ g)(x) = f(g(x)) and is read as "f of g of x". Here, g is the inner function and f is the outer function.
• (g ∘ f)(x) = g(f(x)) and is read as "g of f of x". Here, f is the inner function and g is the outer function.

How to Solve Composite Functions?

Using BODMAS, we always first simplify whatever is within brackets. So to find f(g(x)), first g(x) has to be calculated and is to be substituted within f(x). In the same way, to find g(f(x)), first f(x) has to be calculated and is to be substituted in g(x). i.e., while finding the composite functions, the order matters. It means f(g(x)) may NOT be equal to g(f(x)). For any two functions f(x) and g(x), we find the composite function f(g(a)) using the following steps:

• Find g(a) by substituting x = a in g(x).
• Find f(g(a)) by substituting x = g(a) in f(x).

We can understand these steps using the example below. Here we are finding f(g(-1)) when f(x) = x² - 2x and g(x) = x - 5.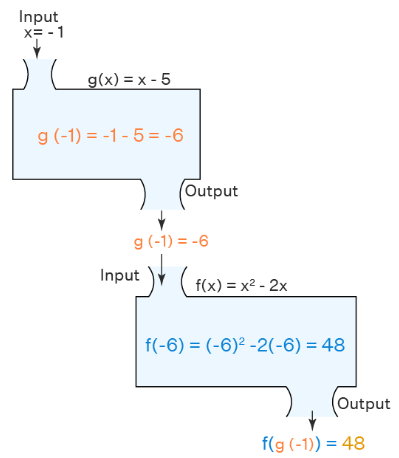

We can summarize this process by simple mathematics calculation as shown below:
f(g(-1)) = f(-1-5)
= f(-6)
= (-6)2 - 2 (-6)
= 36 + 12
= 48

Finding Composite Function From Graph

To find the composite function of two functions (which are not defined algebraically) shown graphically, we should recall that if (x, y) is a point on a function f(x) then f(x) = y. Using this, to find f(g(a)) (i.e., f(g(x)) at x = a):

• Find g(a) first (i.e., the y-coordinate the on the graph of g(x) that corresponds to x = a)
• Find f(g(a)) (i.e., the y-coordinate on the graph of f(x) that corresponds to g(a))

Example: Find f(g(5)) from the following graph.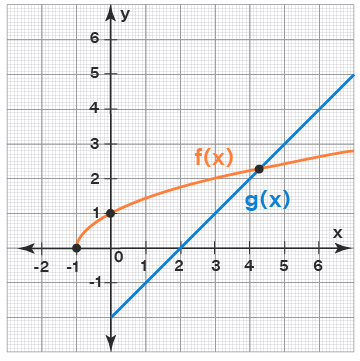

f(g(5)) = f(3) (Because g(5) = 3 as (5, 3) is on g(x))
= 2 (Because f(3) = 2 as (3, 2) is on f(x))
Hence, f(g(5)) = 2.

Finding Composite Function From Table

We have already seen how to find the composite function when a graph of functions is given. Sometimes the points on the graph of functions are shown by tables. So we apply the same procedure as explained in the previous section.

Example: Find g(f(-3)) using the following tables.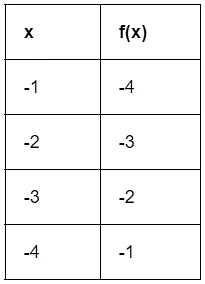

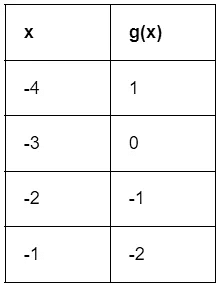
From the table of f(x), f(-3) = -2.
So g(f(-3))= g(-2).
From the table of g(x), g(-2) = -1.
Thus, g(f(-3)) = -1.

Domain of Composite Functions

In general, if g : X → Y and f : Y → Z then f ∘ g : X → Z. i.e., the domain of f ∘ g is X and its range is Z. But when the functions are defined algebraically, here are the steps to find the domain of the composite function f(g(x)).

• Find the domain of the inner function g(x) (Let this be A)
• Find the domain of the function obtained by finding f(g(x)) (Let it be B)
• Find the intersection of A and B and A ∩ B gives the domain of f(g(x))

Example: Find the domain of f(g(x)) when f(x) = 1/(x+2) and g(x) = 1/(x+3).

In f(g(x)), the inner function is g(x) and its domain is A = {x | x ≠ -3}.
Now we will calculate f(g(x)).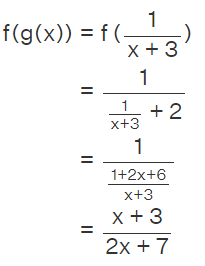

Its domain is B = {x : x ≠ -7/2}
Thus, the domain of f(g(x)) is, A ∩ B = {x : x ≠ -3 and x ≠ -7/2}.
This in the interval notation is (-∞, -7/2) U (-7/2, -3) U (-3, ∞).

Range of Composite Functions

The range of composite function is calculated just like the range of any other function. It doesn't depend on the inner or outer functions. Let us calculate the range of f(g(x)) that was shown in the last example. We got f(g(x)) = 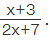Assume that y = 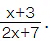This is a rational function. Hence we solve it for x and set the denominator not equal to zero to find the range.
(2x + 7) y = x + 3
2xy + 7y = x + 3
2xy - x = 3 - 7y
x (2y - 1) = 3 - 7y
x = (3 - 7y) / (2y - 1)
For range, 2y - 1 ≠ 0 which gives y ≠ 1/2.
Therefore, range = {y : y ≠ 1/2}.