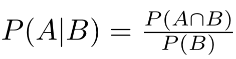Concept of Probability
The concept of probability is difficult to define in precise terms. In ordinary language, the word probable means likely or chance. The probability theory is an important branch of mathematics. Generally the word, probability, is used to denote the happening of a certain event, and the likelihood of the.occurrence of that event, based on past experiences. By looking at the clear sky, one will say that there will not be any rain today. On the other hand, by looking at the cloudy sky or overcast sky, one will say that there will be rain today. In the earlier sentence, we aim that there will not be rain and in the latter we expect rain. On the other hand a mathematician says that the probability of rain is 0 in the first case and that the probability of rain is 1 in the second case. In between 0 and 1, there are fractions denoting the chance of the event occurring.
If a coin is tossed, the coin falls dawn. The coin has two sides ; head and tail. On tossing a coin, the coin may fall down either with the head up or tail up. A coin, on reaching the ground, will not stand on its edge or rather, we assume ; so the probability of the coin coming down is 1. The probability of the head coming up is 50% and the tail coming up is 50% ; in other words we can say the probability of the head or the tail coming up is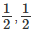 
ince ‘head’ and ‘tail’ share equal chances. The probability that it will come down head
or tail is unity.
The 3 types of probability
Above introduced the concept of a random variable and some notation on probability. However, probability can get quite complicated. Perhaps the first thing to understand is that there are different types of probability. It can either be marginal, joint or conditional.
Marginal Probability: If A is an event, then the marginal probability is the probability of that event occurring, P(A). Example: Assuming that we have a pack of traditional playing cards, an example of a marginal probability would be the probability that a card drawn from a pack is red: P(red) = 0.5.
Joint Probability: The probability of the intersection of two or more events. Visually it is the intersection of the circles of two events on a Venn Diagram (see figure below). If A and B are two events then the joint probability of the two events is written as P(A ∩ B). Example: the probability that a card drawn from a pack is red and has the value 4 is P(red and 4) = 2/52 = 1/26. (There are 52 cards in a pack of traditional playing cards and the 2 red ones are the hearts and diamonds). We’ll go through this example in more detail later.
Conditional Probability: The conditional probability is the probability that some event(s) occur given that we know other events have already occurred. If A and B are two events then the conditional probability of A occurring given that B has occurred is written as P(A|B). Example: the probability that a card is a four given that we have drawn a red card is P(4|red) = 2/26 = 1/13. (There are 52 cards in the pack, 26 are red and 26 are black. Now because we’ve already picked a red card, we know that there are only 26 cards to choose from, hence why the first denominator is 26).
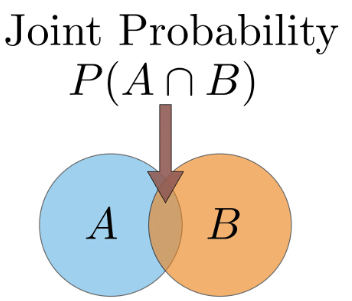
Venn diagram showing the ‘space’ of outcomes of 2 events A and B. In the diagram the 2 events overlap. This overlap represents the joint probability, i.e. the probability of both event A and event B happening. If there was no overlap between the events then the joint probability would be zero.
Linking the probability types: The general multiplication rule
The general multiplication rule is a beautiful equation that links all 3 types of probability:
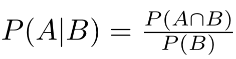
Further explanation of the examples
Sometimes distinguishing between the joint probability and the conditional probability can be quite confusing, so using the example of picking a card from a pack of playing cards let’s try to hammer home the difference.
In the case where we want to find the probability of picking a card that is red and a 4 i.e. the joint probability P(red and 4) I want you to imagine having all 52 cards face down and picking one at random. Of those 52 cards, 2 of them are red and 4 (4 of diamonds and 4 of hearts). So the joint probability is therefore 2/52 = 1/26
In the case where we want to find the probability of picking a card that is 4 given that I know the card is already red i.e. the conditional probability, P(4|red), I want you to again imagine having all 52 cards. However, before picking a card at random you sort through the cards and select all of the 26 red ones. Now you put those 26 cards face down and pick a card randomly. Again, 2 of those red cards are 4’s so the conditional probability is 2/26 = 1/13
Alternatively, if you prefer the maths, we can use the general multiplication rule that we defined above to calculate the joint probability. We first rearrange to make the joint probability, P(A ∩ B), the subject of the equation (in other words, lets put P(A ∩ B) on the left hand side of the equals sign and put everything else on the right). After rearranging we get P(A ∩ B) = P(A|B) ✕ P(B). Let A be the event that the card is a 4 and B is the event that the card is red. P(A|B) = 1/13 as we said above and P(B) = 1/2 (half of the cards are red). Therefore P(A ∩ B) = 1/13 ✕ 1/2 = 1/26.
Probability rules: ‘and’ and ‘or’
‘and’ rule
We’ve already seen the ‘and’ scenario disguised as joint probability, however we don’t yet know how to calculate the probability in the ‘and’ scenario. So let’s go through an example. Let’s suppose we have two events: event A — tossing a fair coin, and event B — rolling a fair die. We might be interested in knowing the probability of rolling a 6 and the coin landing on heads. So to calculate the joint probability of rolling a 6 and the coin landing heads we can rearrange the general multiplication rule above to get P(A ∩ B) = P(A|B) ✕ P(B). We know that event A is tossing a coin and B is rolling a die. So P(A|B) term asks “what is the probability of the coin landing on heads given that I’ve rolled a 6 on the die?” This is where we intuitively understand that the outcome of tossing the coin doesn’t depend on the roll of the die. The events are said to be independent. In this scenario the result of the coin toss would be the same no matter what we rolled on the die. Mathematically we express this as P(A|B) = P(A). Therefore when the events are independent, the joint probability is just the product of the individual marginal probabilities of the events: P(A ∩ B) = P(A) ✕ P(B). So P(coin landing heads and rolling a 6) = P(A=heads, B=6) = 1/2 ✕ 1/6 = 1/12.
Notice that I wrote P(A=heads, B=6). The comma between the events is shorthand for joint probability (you will see this written in the literature).
It should be noted that in many real world scenarios events are assumed to be independent even when this is not the case in reality. This is mainly because it makes the maths a lot easier. The bonus is that the results are often very useful. The Naive Bayes’ method is possibly the most common example of this in data science and typically gives fairly good results in text classification problems.
‘or’ rule
With the ‘and’ rule we had to multiply the individual probabilities. When we’re in the ‘or’ scenario we have to add the individual probabilities and subtract the intersection. Mathematically we write this as P(A ∪ B) = P(A) + P(B) - P(A ∩ B). Why do we have to do this you ask? Well it goes back to the Venn diagram in the above figure. If we add the circle for A and the circle for B then it means that we’re adding the intersection twice. Therefore we need to subtract the intersection.
So let’s change our example above to find the probability of rolling a 6 or the coin landing on heads. This is P(coin landing heads or rolling a 6) = P(A=heads ∪ B=6) = 1/2 + 1/6 - 1/12 = 6/12 + 2/12 - 1/12 = 7/12
Note that the ∪ symbol is known as ‘union’ and is used in the ‘or’ scenario.
There are occasions when we don’t have to subtract the intersection. This happens when the two circles in the Venn diagram don’t overlap. When the circles for two events do not overlap we say that these events are mutually exclusive. This implies that the intersection is zero, written mathematically as P(A ∩ B) = 0. Let’s do an example that covers this case. Suppose we roll a die and we want to know the probability of rolling a 5 or a 6. These events are mutually exclusive because I can’t roll a 5 and a 6. Therefore, their circles in a Venn diagram do not overlap. So the probability of rolling a 5 or a 6 is equal to 1/6 + 1/6 = 2/6 = 1/3 (we haven’t subtracted anything).
ince ‘head’ and ‘tail’ share equal chances. The probability that it will come down head
