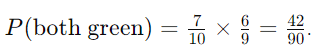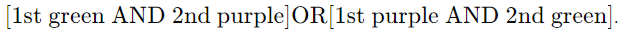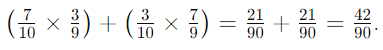Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Conditional Probability
Conditional Probability | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Conditional Probability
What is conditional probability?
- Conditional probability refers to the probability of an event occurring given that another event has already happened.
- An example is drawing names from a hat without replacement:
- The probability of drawing a specific name first is 1/10.
- The probability of drawing a specific name second is 1/9, unless it was already drawn first, in which case it is 0.
- Conditional probabilities change based on prior events.
- These probabilities can be illustrated using Venn diagrams, tree diagrams, or two-way tables.
- However, diagrams are not always necessary and can sometimes be bypassed for simpler questions.
- Conditional probability questions often include phrases like "given that".
- Example: Finding the probability of rain today given that it rained yesterday.
- The "given that" context can affect the probability.
- Conditional probabilities are sometimes denoted using the notation 𝑃(𝐴∣𝐵)P(A∣B), read as "the probability of A given B".
- Example: P(passes∣no revision) indicates the probability of passing given no revision, which differs from P(passes∣lots of revision).
Combined Conditional Probabilities
What are combined conditional probabilities?
- Trickier probability questions often involve both conditional and combined probabilities.
- An example is drawing multiple counters of different colors from a bag without replacement.
- These are known as 'without replacement' questions.
- Multiple draws require combined probabilities to determine outcomes, such as drawing two counters of the same color.
- The outcome of each draw affects the probabilities of subsequent draws, necessitating the use of conditional probability to find the answers.
How do I answer combined conditional probability questions?
- Combine ideas of combined and conditional probability appropriately.
- Use the AND (×) and OR (+) rules from combined probability.
- Remember, events must be independent to use AND, and mutually exclusive to use OR.
- Probabilities for subsequent events change based on conditional probability.
- Example: Drawing counters from a bag without replacement changes probabilities for each draw.
- Consider a bag with 7 green and 3 purple counters.
- Draw one counter, record its color, then draw a second without replacing the first.
- Probability both counters are green:
- Probability the first counter is green: 7/10.
- If the first is green, probability the second is green: 6/9.
- This demonstrates the conditional probability concept.
- To find 𝑃(both green)P(both green), multiply the two probabilities:
- This demonstrates the combined probability concept.
What about when two things are happening at the same time?
- Sometimes a question may not explicitly state the sequence of events.
- For example, it might simply say that two counters are drawn from a bag, without mentioning the order.
- You can assume that events happen one after the other for simplicity.
- This assumption does not change the mathematics of the question but makes it easier to solve.
- For example, drawing two counters from a bag can be treated as drawing one counter and then a second without replacement.
- This allows you to break down the problem into finding the probability of the 'first counter' and the 'second counter'.
- Drawing two counters simultaneously is mathematically equivalent to drawing them sequentially without replacement.
Are there any useful shortcuts for combined conditional probability questions?
- Consider a bag with 7 green counters and 3 purple counters. If 2 counters are drawn without replacement, we can determine the probability of the two counters being of different colors using the AND/OR rule.
- This involves considering '[1st green AND 2nd purple] OR [1st purple AND 2nd green]' to calculate the desired probability.
- Considering a bag with 7 green counters and 3 purple counters.
- Drawing 2 counters without replacement.
- Utilizing the AND/OR rule - '[1st green AND 2nd purple] OR [1st purple AND 2nd green]' - for calculating the probability of two counters being of different colors.
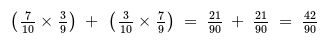
Understanding Probabilities: A Simplified Explanation
- Consider a bag with 7 green and 3 purple counters, and 2 counters are drawn without replacement.
- To find the probability of drawing counters of different colors, use the AND/OR rule:
- Notice both AND probabilities are equal (21/90).
- This is because the numerators and denominators are the same but swapped.
- Another way:
- There are two ways for different colors (green then purple, or purple then green).
- Each way has the same probability
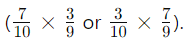
- Therefore, the probability is
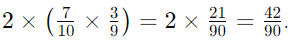
- This method is useful for more complex scenarios.
- Example: Probability of drawing 2 green and 2 purple counters from the same bag when drawing 4 counters without replacement:
- Using the AND/OR method requires considering multiple sequences, like
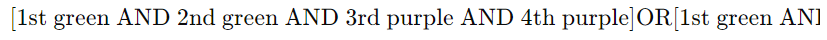 OR
OR 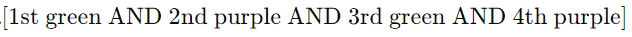 ,etc.
,etc. - There are six such sequences to consider.
- Using the AND/OR method requires considering multiple sequences, like
- Simplified method:
- There are 6 ways for '2 green and 2 purple' to occur (GGPP, GPGP, GPPG, PPGG, PGPG, PGGP).
- Each way has the same probability:
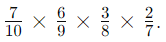
- Therefore, the probability is
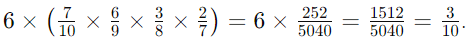
The document Conditional Probability | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
66 videos|674 docs|19 tests
|
Related Searches